基于神经网络观测器的卫星姿态控制系统陀螺故障诊断

，，，

(航天工程大学 航天信息学院,北京 101416)

0 引言

航天器是一种结合多个领域尖端技术的大型复杂系统，其对国民经济、科技等活动有着重要的影响。航天器所处的特殊空间环境不仅使得其面临的故障情况十分复杂，同时难以进行诊断和维修。因此，开展航天器的故障研究具有重要的社会经济效益和工程价值[1]。

基于解析模型的方法是目前研究最为活跃的方法[2-3]。文献[4-5]研究了鲁棒观测器，设计产生对扰动解耦的观测器残差，但是无法完全解耦。与鲁棒观测器类似，文献[6-8]提出的学习观测器虽然对空间干扰和测量噪声具有鲁棒性，但是也没有完全与故障残差解耦。文献[9-10]研究了自适应观测器方法，通过对故障的自适应估计使得观测结果对扰动鲁棒，但是观测器设计复杂，增益矩阵计算困难。

神经网络具有优秀的非线性建模能力，因此被用于故障诊断。文献[11-12]提出应用神经网络对系统中的非线性部分进行估计，放宽了对系统的匹配条件，但是没有充分利用系统的结构知识；文献[13-15]提出了应用神经网络直接估计执行器故障的方法，没有考虑陀螺故障的情况。

为了实现对陀螺故障的检测、隔离与估计，在利用模型知识的同时降低观测器的设计难度，本文提出一种基于神经网络观测器的陀螺故障诊断方法，利用系统内的冗余关系实现对陀螺故障的检测和隔离，同时利用神经网络的万能逼近性实现对故障的估计。

1 问题描述

1.1 姿态控制系统建模

考虑如图1所示的三轴稳定卫星姿态控制系统。卫星姿态控制系统可以分为运动学子系统和动力学子系统[16]。运动学子系统包括陀螺、星敏感器和运动学过程；动力学子系统包括反作用飞轮、陀螺和动力学过程。控制律为四元数反馈控制律。仅考虑陀螺出现故障的情况。

图1 卫星姿态控制系统

由四元数描述的姿态运动学方程为[16]：

(1)

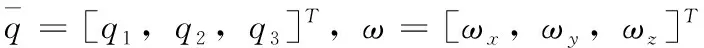
(2)

选取x1=[q0,q1,q2,q3]T为状态变量，则姿态运动学方程可以写成如下所示的状态空间形式：

(3)

其中:u1=[ωx,ωy,ωz]T为运动学输入；y1=[q0,q1,q2,q3]T为运动学输出；φ(x1,u1)为运动学非线性函数。

(4)

考虑陀螺的测量误差，则运动学子系统观测方程可以表达如下：

(5)

其中:b=[bx,by,bz]T为陀螺的测量误差，包括常值漂移和随机噪声。

将卫星本体看作刚体，则由刚体运动的动量矩公式可得到如下的卫星姿态动力学方程[16]：

(6)

其中:H为卫星的角动量；τ=(τx,τy,τz)T为卫星本体受到的合力矩在本体坐标系中的分量；ω=[ωx,ωy,ωz]T为卫星本体的角速度在本体坐标系下的分量；

(7)

角动量H可以表示为H=Iω，其中I为卫星的转动惯量矩阵，通常情况下，卫星的惯性主轴与卫星本体坐标系重合时，则有I=dig{Ix,Iy,Iz}。考虑卫星在空间环境中受到的干扰力矩，则式(5)可以写做如下形式：

(8)

其中:τc=(τcx,τcy,τcz)T为执行器产生的控制力矩；τd=(τdx,τdy,τdz)T为卫星受到的干扰力矩。

选取x2=[ωx,ωy,ωz]T为状态变量，则动力学子系统可以写成如下所示的状态空间形式：

(9)

其中:u2=[τcx,τcy,τcz]T为动力学子系统的输入；y2=[ωx,ωy,ωz]T为动力学子系统的输出；d=[τdx,τdy,τdz]T为干扰力矩；b=[bx,by,bz]T为陀螺的测量误差；φ(x2)为动力学子系统的非线性函数。

(10)

系统的输入矩阵、输出矩阵和扰动分布矩阵如下：

1.2 问题分析

为方便分析，对系统做以下合理假设。

假设1：假设卫星工作在小角度机动状态下，因此式(3)和式(9)中的非线性函数均为满足Lipschitz条件的Lipschitz函数，即:

(11)

假设2：不同部件不会同时发生故障。

假设3：故障和扰动均有界，且故障的变化速率有界。

其中，假设1是采用观测器方法的前提；假设2通常情况下是可以满足的，因为飞轮、陀螺和星敏感器为独立部件，同时故障的概率较小；假设3反应的是实际系统是能量有限的，不会出现变化率为无穷大的突变。

观察式(5)和式(9)，陀螺的测量值为运动学方程的输入和动力学方程的输出。因此运动学子系统和动力学子系统间存在冗余关系，运动学子系统能反映陀螺和星敏感器间的关系，动力学子系统能反应陀螺和反作用飞轮间的关系。利用这种冗余关系可以对陀螺故障进行检测和隔离。

本文仅考虑加性故障，故障模型如下：

uout=u+f

(12)

其中:u为正常信号；uout为故障后信号；f为故障参数，可以是一个突变常数，也可以是一个时变参数。则故障后的卫星姿态控制系统观测模型为：

(13)

(14)

各符号意义与前文一致。

2 基于神经网络的陀螺故障检测与估计

基于解析模型的观测器方法通常需要分别设计故障检测观测器和故障估计观测器，同时需要设计复杂的解耦方法，使得设计的观测器只对特定故障敏感。为简化设计过程，在一定模型知识的前提下采用神经网络对故障直接进行估计。根据1.2节的分析，运动学子系统和动力学子系统间存在着冗余关系，分别针对运动学子系统和动力学子系统设计陀螺故障观测器，根据冗余关系就可以避免其他故障对检测结果的影响。

2.1 基于运动学的陀螺故障观测器设计

考虑无故障下运动学子系统的观测方程式(3)以及陀螺故障情况下的运动学子系统状态方程式(13)，采用神经网络对陀螺故障参数进行估计，可以得到如下的故障观测器：

(15)

(16)

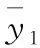
(17)

根据神经网络的逼近特性，存在一组理想权值和阈值使得f可以表示为如下形式：

(18)

由式(13)和式(15)可以得到观测误差动态方程如下：

(19)

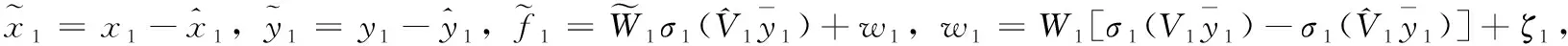
神经网络观测器设计的关键之处在于寻找合适的神经网络权值更新律和观测器增益使得观测器能够稳定收敛，即观测误差应渐近趋向于零。参照经典的误差反向传播算法，给出如下的神经网络权值更新律：

(20)

(21)

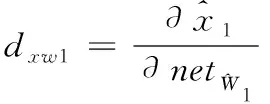
(22)

则得到最终的神经网络权值更新律为:

(23)

定理1：考虑如式(13)形式的动态系统，构造如式(15)的故障观测器，以式(19)定义观测误差。对于给定常数γ0，如果存在矩阵M和对称正定矩阵Q满足：

(24)

观测器增益选为L1= -MC1-1，采用式(23)为神经网络的权值更新律，则观测误差一致有界，且神经网络权值估计误差有界。

证明：选择如下正定Lyapunov函数：

(25)

(26)

注意到以下不等式成立：

(27)

将式(11)和式(27)代入式(26)得：

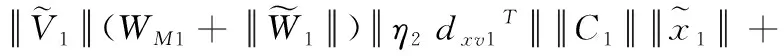
(28)

(29)

证毕。

定理1:给出了保证神经网络观测器稳定的观测器增益选取方法，具体设计时可以通过求解定理1内式(35)给出的线性矩阵不等式来确定观测器增益的值。需要注意的是神经网络参数的选择，由于神经网络的黑箱性质，通常参数的选择依靠经验进行调节，基本原则是在一定精度情况下使神经元数量尽可能的少；当学习曲线震荡变大时，减小学习率。

2.2 基于动力学的陀螺故障观测器设计

考虑陀螺故障情况下的动力学子系统状态方程式(14)，采用神经网络对陀螺故障参数进行估计，可以得到如下的故障观测器：

(30)

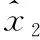
(31)

根据神经网络的逼近特性，存在一组理想权值和阈值使得f可以表示为如下形式：

(32)

由式(14)和式(30)可以得到观测误差动态方程如下：

(33)

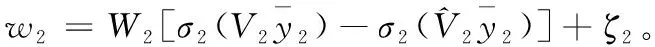
与2.1节相同，需要寻找合适的神经网络权值更新律和观测器增益使得设计的观测器能够稳定收敛。与式(23)类似的给出如下权值更新律：

(34)

定理2:考虑如式(14)形式的动态系统，构造如式(30)的故障观测器，以式(33)定义观测误差。对于给定常数γ0，如果存在矩阵M和对称正定矩阵Q满足：

(35)

观测器增益选为L1= -MC1-1，采用式(34)为神经网络的权值更新律，则观测误差一致有界，且神经网络权值估计误差有界。

证明过程同定理1。定理2的作用与定理1相同，都是给出了保证神经网络观测器稳定的条件，参数的求取也是类似的，求取式(35)的线性矩阵不等式即可。两者的区别在于扰动在系统状态方程的不同位置，因此对于观测误差的影响不同，最终保持观测器稳定的边界条件也有所区别。

2.3 故障决策

通常基于观测器的故障诊断方法通过产生残差进行故障诊断，本文中则直接以神经网络的故障估计值为故障诊断依据。由式(13)、式(14)、式(15)和式(30)可以看出，当存在执行器故障和星敏感器故障时，会对陀螺故障估计结果形成干扰，由单一的观测器结果不能判断故障的准确位置。由1.2节可知，陀螺的测量值为运动学方程的输入和动力学方程的输出，即运动学子系统和动力学子系统存在冗余关系。如果发生星敏感器故障，则会影响运动学子系统观测器的估计值，但不会影响动力学子系统观测器；如果发生执行器故障，则会影响动力学子系统观测器的估计值，但不会影响运动学子系统观测器。利用这一冗余关系容易得到如下的故障决策逻辑：

(36)

由式(19)和式(33)可以看出观测器受到扰动力矩和陀螺测量误差的影响，同时由于神经网络的估计存在误差，当没有故障时，神经网络的输出应为扰动、估计误差共同作用下的稳定小值；当发生故障时，神经网络的输出为故障的估计值。因此该方法只能估计大于扰动干扰的陀螺故障。阈值的选取取决于扰动对系统的干扰情况。

3 算例结果与分析

仿真所需参数如下：卫星的惯量矩阵为I=diag{930,800,1070}kg·m2；初始轨道角速度为ω0=7.3×10-5rad/s；初始姿态角速度ω(0)=[0,0,7.3]T×10-5rad/s；初始姿态为Q0=[0.9786,-0.0704,-0.1798,0.0704]T；干扰力矩为τd=[Axsinωdt,Aysinωdt,Azsinωdt]T，其中Ax=1.4e-5N·m，Ay=1.5e-5 N·m，Az=1.6e-5 N·m，ωd=0.02 rad/s；陀螺常值漂移为8.72e-5 rad/s，噪声为高斯白噪声N(0,10-7)；控制器参数为Kp=[40,40,40]T，Kd=[1000,1000,1000]T。由式(16)，基于运动学的故障观测器采用3层神经网络，其中输入层4个神经元，隐藏层14个神经元，输出层3个神经元，学习率η1=η2=20，ρ1=ρ2=1e-7；由式(31)，基于动力学的故障观测器采用3层神经网络，其中输入层3个神经元，隐藏层10个神经元，输出层3个神经元，学习率η3=η4=10，ρ3=ρ4=1e-6。

系统仿真长度为400 s，步长为0.01 s，设置故障时刻为200 s。以X轴故障为例，分别设置3个故障案例。案例1为陀螺常值漂移故障f=0.0001 rad/s；案例2为执行器恒差故障f=0.001 N；案例3为星敏感器卡死故障，输出固定为Q=[1,0,0,0]。

根据无故障情况下的估计情况，设定阈值为ε1=1e-4，ε2=6e-5；δ1=2.5e-4，δ2=1.5e-4。

图2为案例1故障诊断结果，其中图2(a)为基于运动学的故障观测器估计结果；图2(b)为基于动力学的故障观测器估计结果。根据式(36)可以确定发生陀螺故障，故障估计值的相对变化大小与故障值近乎相同。

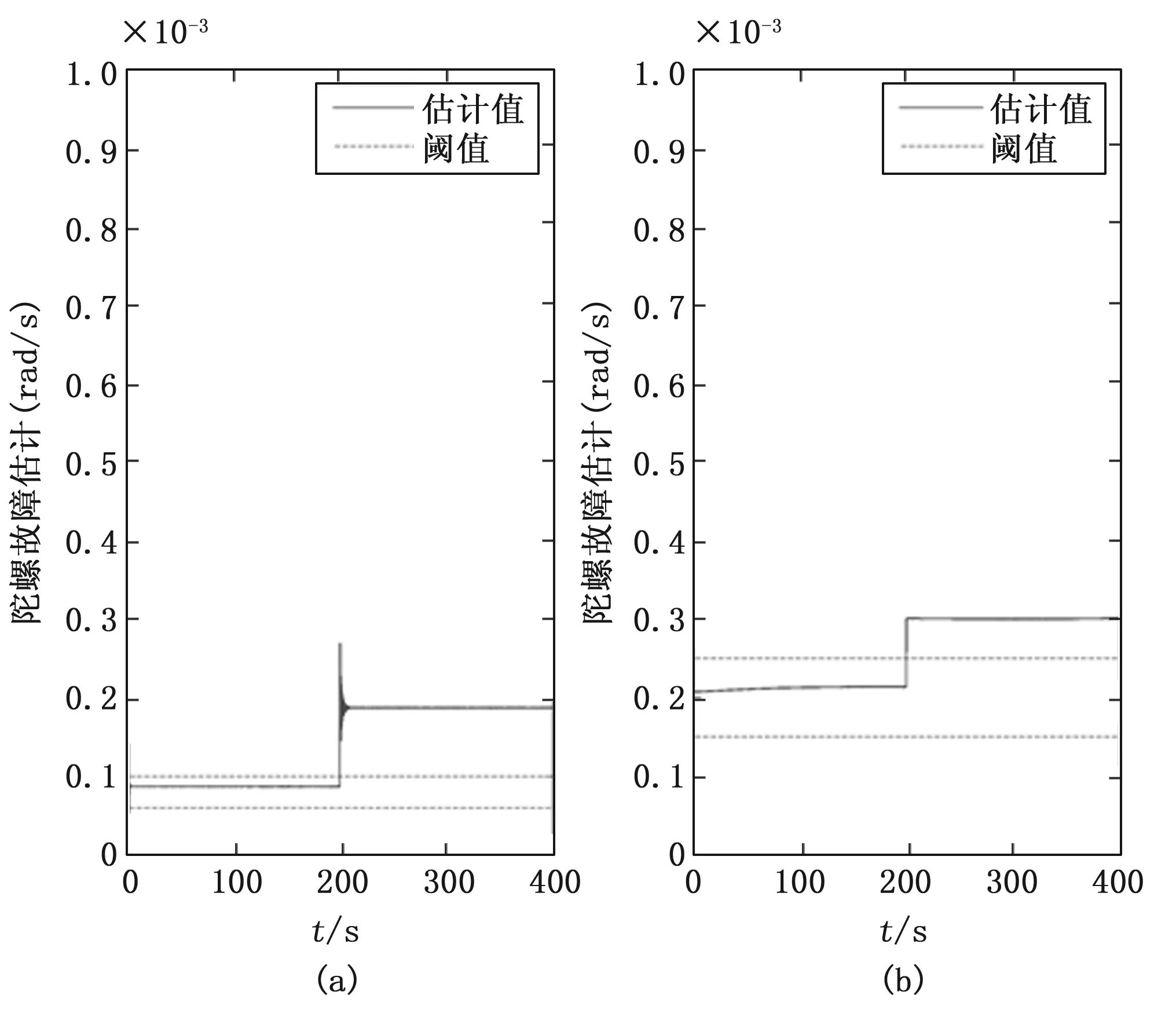
图2 案例1故障诊断结果

图3为案例2故障诊断结果，其中图3(a)为基于运动学的故障观测器估计结果；图3(b)为基于动力学的故障观测器估计结果。根据式(36)可以确定发生执行器故障。

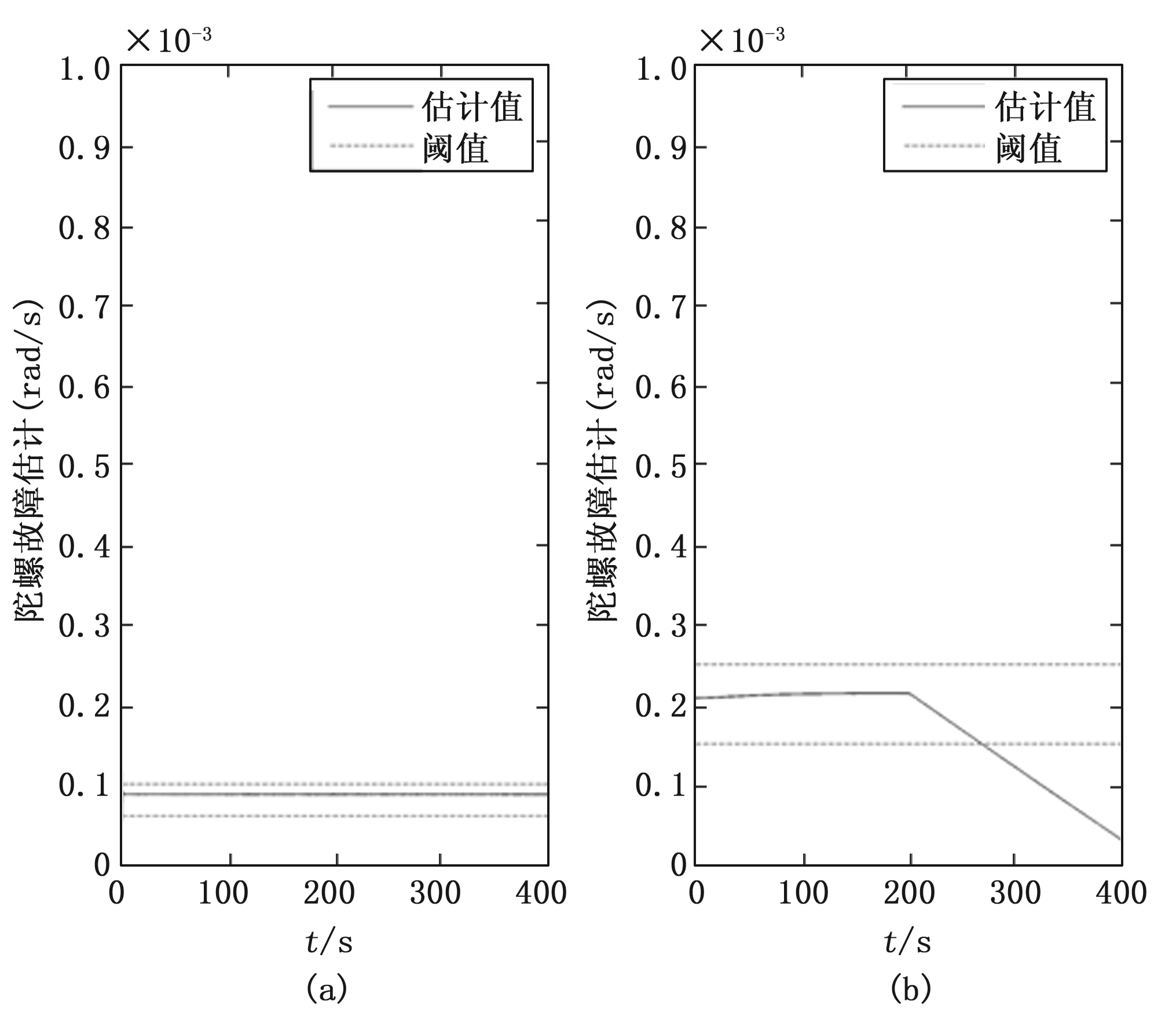
图3 案例2故障诊断结果

图4为案例3故障诊断结果，其中图4(a)为基于运动学的故障观测器估计结果；图4(b)为基于动力学的故障观测器估计结果。根据式(36)可以确定发生星敏感器故障。

图4 案例3故障诊断结果

由3个仿真案例可以看出，在检测到陀螺故障的前提下，由两个观测器估计结果的相对变化情况即可得到故障程度的估计，后续可以考虑采用kalman滤波等信息融合算法对两个观测器的估计结果进行最优化估计，以便减少噪声的影响。

4 结束语

1)利用运动学子系统与动力学子系统特的冗余关系，设计了陀螺故障检测和隔离的逻辑，实现了对陀螺故障的估计。

2)观测器采用神经网络与模型相结合的方法设计，与一般观测器相比有更高的设计裕量，但是算法运算量较大，实时性较弱。

3)以三轴稳定卫星姿态控制系统为例，仿真结果表明所提方法的故障诊断能力。