光学电压传感器分压结构的缺陷及改进方法

黄奕钒, 徐启峰, 陈 昊, 许志坤

(福州大学电气工程与自动化学院, 福建省福州市 350116)

0 引言

光学电压传感器(optical voltage sensor,OVS)的测量原理多基于Pockels效应，即在外加电场的作用下，线偏振光在电光晶体内传播一定距离后产生相位延迟[1-4]。通常认为现有的技术还不能直接测量相位延迟，因此借助于偏光干涉检测模式，将相位延迟转换为光强变化，通过检测光强的大小间接测量电压[4-6]。这一方法存在以下问题。①仅能近似线性地测量有限的电光相位延迟。以OVS必须具备的0.2级准确度为例，理论上可测量的相位延迟小于6.28°[1,6]，工程应用中需要留出一定的裕度，因此一般将相位延迟控制在3°以内。②晶体半波电压对互感器测量范围与测量灵敏度的限制。在相同的电场强度作用下，半波电压越大，越有利于扩大测量范围；半波电压越小，越有利于提高测量灵敏度[1]。因此，晶体的半波电压限制使测量范围与测量灵敏度难以兼顾。

目前工程上有两个解决半波电压限制的方法。一个是通过电容分压，并采用锗酸铋(BGO)晶体作为敏感元件[7]。但是，这一方法带来电容老化、分压比漂移等问题，同时削弱了OVS光隔离的优势[8-9]。第二个方法是应用多片晶体叠层结构，例如：采用8片晶体的叠层结构可以将整体半波电压提高到6.87 MV[10]。但是，这一方法仅能满足1 000 kV电压等级的分压要求，其工程实用性受到很大限制。同时，震动与热胀冷缩等因素不可避免地使光路和光学器件的相互位置产生偏移，导致测量误差[2,11-12]。例如：在8片晶体叠层结构中，入射光偏移0.5°时产生约0.202%的测量误差，晶体之间相互偏移0.5°时产生约0.275%的测量误差，不容忽视。

本文对多片晶体叠层结构进行了改进，使其可以适用于110 kV电压等级。

1 多片晶体叠层结构分析

多片晶体叠层结构的纵向调制OVS[10]如附录A图A1所示。该结构的半波电压Vπ为[10]：

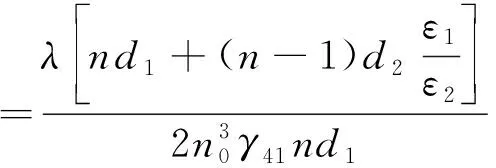
(1)

式中：d1，d2分别为晶体和SF6气体的厚度,d1=1 mm，d2=14.6 mm；ε1，ε2分别为BGO晶体和SF6气体的相对介电常数，ε1≈16.3ε2；晶体的片数n=8、折射率n0=2.098、线性电光系数γ41=1.03×10-12。光源波长λ=632.8 nm时，Vπ=6.87 MV，是单片BGO晶体半波电压的198倍。这一结构存在以下两个问题。

1)不适用于500 kV及以下电压等级。纵向调制下晶体半波电压Uπ与相位延迟φ的关系为：

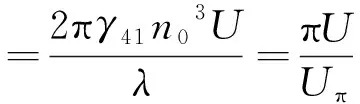
(2)

式中：U为待测电压。当λ=632.8 nm时，Uπ=33.26 kV。

根据式(3)：

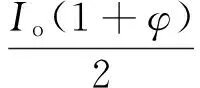
(3)

近似线性sinφ≈φ导致的测量误差：

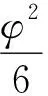
(4)

对于0.2级测量准确度，需要满足：

<0.2%

(5)

得φ<6.28°，代入式(2)，得U<1.164 kV。由式(2)可知，在相同的电场强度作用下，Uπ越大则φ越小，测量范围越大；而Uπ越小则φ越大，测量灵敏度越高。因此，为了兼顾测量范围与灵敏度，一般将U控制在0.01Uπ～0.018Uπ之间，或U=0.3～0.6 kV。

8片晶体叠层结构中，采用了厚度为1 mm的BGO晶体，每片晶体分压UBGO为：

(6)

式中：V为系统额定电压。

根据式(6)，附录B表B1列出了每一个电压等级下8片晶体叠层结构中单片晶体的平均电压，可见500 kV及以下电压等级均不能满足分压要求。原始文献中[10]，这一结构被用于250 kV交流电压以及400 kV雷电冲击电压的测量，其实并不合理。

由式(6)可知，增加晶体片数n可以提高UBGO，如附录B表B2所示。但是，500 kV及以下电压等级需要54片以上的晶体，缺乏工程实用性。产生这一结果的原因是BGO晶体的介电常数大(为16.3)，SF6绝缘气体的介电常数小(为1.002)，相同的绝缘长度SF6气体比BGO晶体的分压高约16倍。系统额定电压越低，UBGO越小，因此可以通过增加晶体的数量来提高分压比，以满足U为0.3～0.6 kV的工程要求。但也导致OVS传感结构复杂，组装调试困难。事实上，过多的晶体片数还增加了因光路或光学器件偏移引入的误差。

2)光学器件或光路偏移导致测量误差。理论上认为纵向调制OVS的测量结果不受外电场的干扰和极间电场分布不均匀的影响[13-14]。根据Pockels效应，φ与晶体内电场E的关系为：

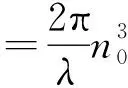
(7)

式中：d为通光方向的厚度。若E为匀强电场，则U=Ed，式(7)可改写为：

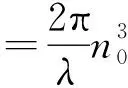
(8)

但是在实际应用中，晶体内电场的分布受到电极的尺寸与形状、绝缘结构以及绝缘介质的影响，使晶体内电场分布不均匀[15]。此外，因震动、元器件连接的老化与热胀冷缩等因素，不可避免地使光路或晶体发生偏移，引入测量误差[11-13]，如图1所示。

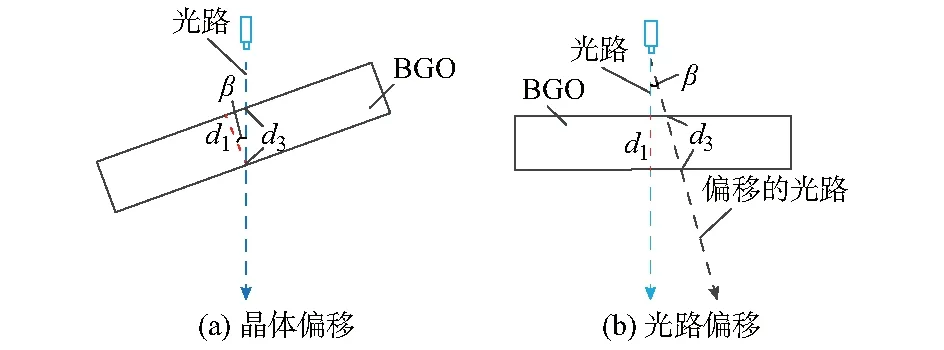
图1 多片晶体层叠结构的偏移情况Fig.1 Deviations in multi-segmented longitudinal modulation OVS

设晶体或光路的偏移角度为β，此时相位延迟φ′为：

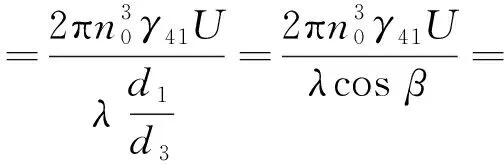
(9)

式中：U′为晶体或光路偏移后的待测电压。则引入的误差为：

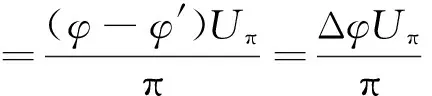
(10)

设总电压误差ΔUTotal为单片晶体的误差ΔUi之和，故称之为积分电压误差。8块晶体同时发生偏移时引入的误差ΔUTotal为：

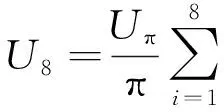
(11)

式中：Δφi为每片晶体引入的相位误差。同理光路偏移时，ΔUTotal为：

(12)

根据式(11)、式(12)可知，测量误差随着晶体片数的增加而增加，因此减少晶体片数有助于减小误差。

利用ANSYS Maxwell软件对电场分布进行仿真分析，假定每片BGO晶体直径10 mm，厚1 mm，晶体之间间隔14.6 mm，电压等级为110 kV。仿真结果如附录A图A2所示，可见晶体内的电场分布极不均匀。造成这一现象的主要原因是BGO晶体的介电常数远大于SF6气体的介电常数，导致晶体内的电场强度小、电势下降慢，晶体外的电场强度大、电势下降快，使晶体边缘电场等位线严重扭曲[11-12]，其中靠近电极侧尤为明显。设晶体之间或光路向右偏移为“+”，向左偏移为“-”，偏移角度范围为±0.5°。利用ANSYS Maxwell软件对光路进行电场积分运算，得到各通光路径上的积分电压。以无偏移光路的积分电压为基准，表1列出了8片晶体发生同向同角度偏移或光路偏移时引入的误差。偏移0.5°时分别为0.275%和0.202%。

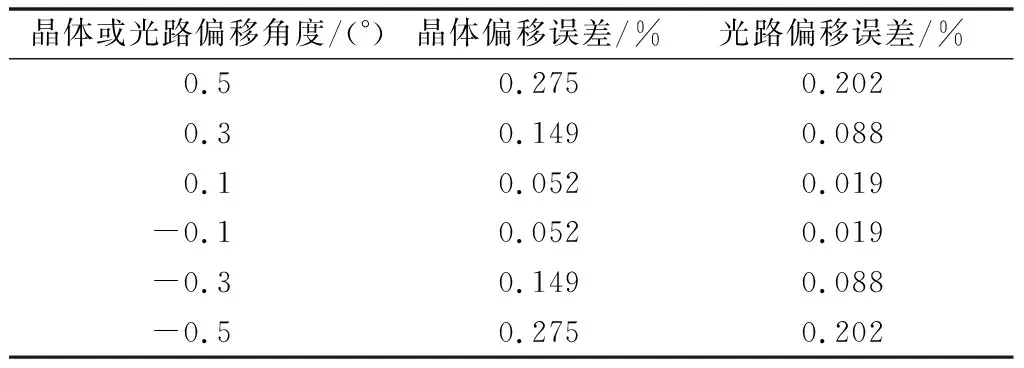
表1 晶体或光路偏移引入的误差Table 1 Error caused by deviation of crystals or optical path

表2列出了上述两种情况下发生0.5°偏移时，每片BGO晶体引入的误差。显然，晶体偏移时的误差主要来自靠近电极的第1，2和第7，8号晶体。光路偏移时位于地电极的8号晶体的误差高达0.582%。而4号和5号晶体处在电极中间位置，此处的电场分布相对均匀，引入的积分电压误差很小。

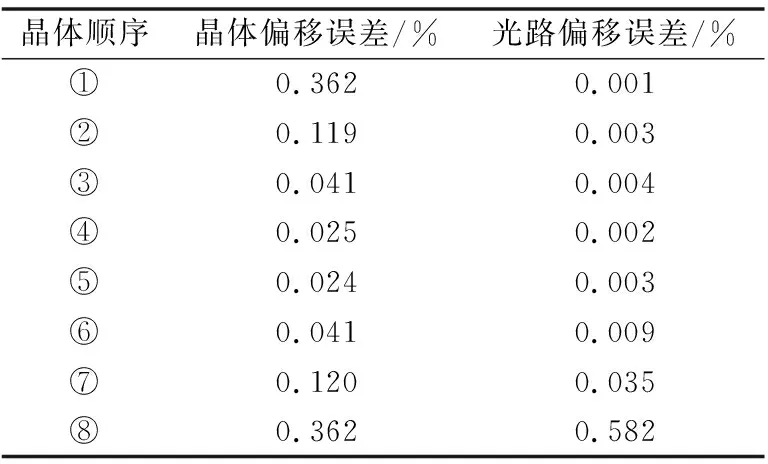
表2 晶体或光路偏移时每片晶体引入的误差Table 2 Error of each BGO crystal plate caused by deviation of crystals or optical path

此外，附录B表B3列出了晶体数量对积分电压误差的影响。采用12片BGO晶体时晶体偏移的最大误差由0.275%上升至0.316%，光路偏移的最大误差由0.202%上升至0.243%。

2 分压结构的改进方法

根据上述分析，多片晶体叠层结构测量易受不均匀电场的影响，且只适用于1 000 kV电压等级。本文提出的新结构能够改善晶体内电场分布，有效地消除偏移误差，并适用于各个电压等级。以110 kV电压等级为例加以介绍。

2.1 结构设计

减小积分电压误差的有效途径之一是将BGO晶体置于两个电极的中间，并且尽量减少晶体片数。

110 kV电压等级下雷电冲击耐受电压为450 kV[16]，绝缘气体SF6在0.1 MPa下击穿场强为89 kV/cm[10]。新结构中电极间距为110 mm，仿真得到最大场强为65 kV/cm，满足绝缘要求。取晶体片数n=1，设晶体的厚度为d，得UBGO为：

(13)

根据U=0.3～0.6 kV，得到d的取值区间为[4.69,9.03]mm。当d=7 mm时，UBGO=457 V，代入式(1)得到半波电压为8.01 MV，满足测量要求，改善后的结构如图2所示。

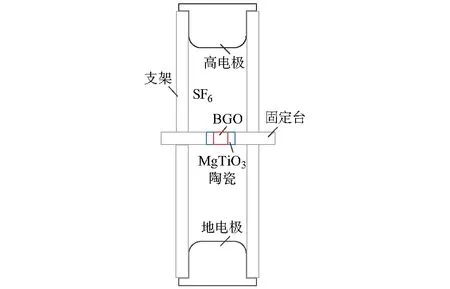
图2 改进方法的结构图Fig.2 Improved structure diagram

其他电压等级下传感系统的参数如附录B表B4所示，可见新结构能够满足各个电压等级下晶体的分压要求。

改进后晶体或光路发生±0.5°偏移时引入的积分电压误差如附录B表B5所示，最大误差为0.149%和0.127%，说明对减少误差有一定的作用。但是，仍然需要进一步降低积分电压误差，通常要小于0.05%，以便整体误差满足0.2%的准确度要求。

产生表B5所示误差的重要原因是BGO晶体与SF6气体的介电常数差别大，导致晶体内外的电场分布严重扭曲，如附录A图A3所示。在晶体外部包裹某种不具有电光效应的绝缘材料[14]，可以平缓因晶体和绝缘气体的介电常数差别过大而引起的电场畸变。包裹介质的介电常数设定为15，电场分布计算结果如附录A图A4所示。比较图A3和图A4可见，后者晶体边角处电场的畸变转移到了包裹的介质上，从而改善了晶体内的电场分布。

为了进一步说明改善的效果，引入标准差来定量描述场强分布的均匀程度，标准差小说明数据集的离散程度小，表明电场分布均匀，积分电压误差小[11-12]。标准差的计算公式为：

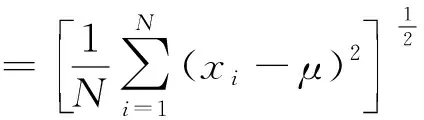
(14)

式中：N为晶体中心线位置矩阵中元素总数；xi为矩阵中第i个元素的场强值；μ为矩阵中总元素的场强平均值。利用ANSYS Maxwell将通光路径分成N=1 001段，并导出每一段的场强值，代入式(12)计算得到包裹介质前、后通光路径上的场强值标准差，分别为4 572和45。标准差降低了两个数量级，说明包裹介质后晶体内电场分布的均匀性得到了明显改善。

为了更好地说明晶体的电场分布，建立了一个基于新结构的3D模型，如图3(a)所示。图3(b)和(c)分别为包裹介质前后晶体上表面的电势分布，可见包裹介质前晶体表面电势分布极不均匀，包裹介质后晶体表面已近似为等势面，说明包裹介质能有效地改善晶体内的电场分布。

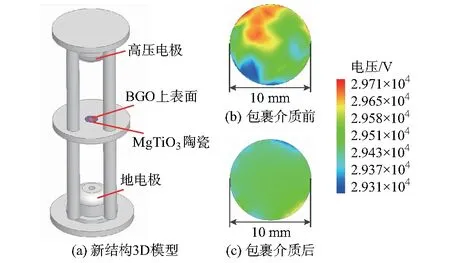
图3 新结构的3D模型及晶体表面的电场计算Fig.3 3D model for new structure and calculations of electric field distributions on crystal surface

2.2 包裹材料的选择

设包裹厚度D=5 mm、介电常数范围为17～25，晶体以及光路发生0.5°偏移时的误差如附录B表B6所示，可见包裹材料的介电常数在20～23为宜。本文选用MgTiO3陶瓷，其介电常数为20，绝缘性能好，原料丰富，成本低廉，介电损耗低，且介电常数温度系数很小[17-18]。

在BGO晶体外侧包裹MgTiO3陶瓷后，晶体分压发生变化。根据电容等效法，BGO晶体与MgTiO3陶瓷的并联电容C1为：

(15)

式中：S为晶体的截面积；S1为包裹介质的环形面积；ε3为MgTiO3陶瓷介电常数；k为静电力常数。

SF6气体的电容表达式C2：

(16)

则UBGO与系统电压等级V的关系满足：

(17)

结合U=0.3～0.6 kV，代入已有数据，得D≥2.3 mm。

选择D在5～6 mm范围内进行仿真分析，结果如附录B表B7所示，D=5.5 mm最佳。图2即为最终确定的新结构。

3 实验验证

实验系统如附录A图A5所示，采用CLD1015光源，波长为980 nm。电极间距为110 mm，晶体尺寸为∅10 mm×7 mm，MgTiO3陶瓷的长度为7 mm，内径10 mm，外径15.5 mm。利用检偏器将电光相位延迟解调后，由CCD光束质量分析仪(BC106N-VIS)测量出射光斑的光强分布。受条件限制，实验中的气体环境为空气，但由于空气与SF6气体的介电常数分别为1.001和1.002，采用空气替代SF6不影响实验结果[11-12]。

由于目前的实验手段无法直接测量晶体表面的电场分布，结合式(3)和式(10)，发生晶体或光路偏移时光功率变化ΔI为：

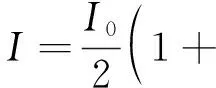
(18)

ΔI与ΔU成正比，ΔI越均匀，说明ΔU越小，对比包裹介质前后出射光功率分布的均匀程度，即可验证方法的有效性。

在室温环境,U=8 kV的条件下，利用光束分析仪采集包裹介质前后出射光斑边缘的光功率分布见如附录A图A6所示。为了避免光斑以外暗底的影响，只截取图像中的部分光斑用MATLAB进行灰度处理，得到直方分布图。包裹介质后，灰度值分布主要集中在75～150范围内，而大于150的光斑像素点明显减少，表明光斑的聚集现象消失，分布更加均匀，与仿真结果一致。两者的灰度值标准差分别为56.06和40.02，同样表明光强分布的均匀性得到改善。

附录A图A7为U=10 kV时整个光斑的光功率分布图，同样进行灰度处理，制成直方分布图并计算标准差(两者分别为53.91和41.96)。显然，包裹介质后光强分布更加均匀，与图3的仿真结果一致。

4 结语

本文对多片晶体叠层结构进行了改进，并以110 kV电压等级为例，简化了传感系统的结构，改善了晶体内电场的分布。仿真计算结果表明，积分电压误差从0.275%降低至0.01%以下，满足0.2级准确度要求。最后，对这一结构进行了实验验证，实验结果与仿真分析一致。改进后的结构同样适用于220，330，500 kV电压等级，但受条件的限制，尚未进行实验验证，后续将对更高电压等级作深入研究。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。