多机系统超低频振荡稳定分析与调速器参数优化

黄 伟, 段荣华, 江崇熙, 周靖皓, 甘德强

(1. 云南电力调度控制中心, 云南省昆明市 650011; 2. 浙江大学电气工程学院, 浙江省杭州市 310027)

0 引言

2016年云南电网与南方电网主网异步联网后,云南电网内部出现多次长时间、超低频的频率振荡现象,即超低频振荡[1-5]。超低频振荡频率小于0.1 Hz(云南电网为0.05 Hz),远低于低频振荡的频率范围。早在20世纪70年代左右,加拿大电网就已发现该问题,鉴于其表现形式为全网机组频率以一个公共的频率共同振荡,有文献将其称为公共模式,以对应低频振荡中的本地模式和区域模式[6-8]。在其他的国内、外电网实际运行中同样出现了类似的频率振荡现象[9-12],与云南电网情况类似,这些电网水电渗透率均较高。

至今,对超低频振荡问题已有基于特征值分析和时域仿真技术的研究[2-5,11-12]。文献[13-14]利用阻尼转矩法解释了超低频振荡的机理。文献[15]提出了一种基于能量流原理的超低频振荡的紧急控制方法。文献[16]提出了基于时域指标和阻尼约束的调速器参数优化方法。文献[17]利用值集法对云南电网的超低频振荡进行了原理分析并提出了改进措施。

已有的研究对超低频振荡问题已经做了较为深入的研究。对超低频振荡发生原因的讨论,本文首先基于奈奎斯特矢量裕度的概念,对多机系统超低频振荡的机理进行了分析,发现水电机组原动机传递函数中存在的右半平面(RHP)零点使其在振荡频率处相位滞后过大是造成超低频振荡的关键原因,解释了超低频振荡为何总发生于水电占优系统。分析的理论基于奈奎斯特判据,保证了分析结果在数学上的严格性。

当系统负荷出现波动时,机组调速器需要快速动作,使机械功率快速跟踪负荷波动,切除机组的调速器会降低系统的跟踪性能。本文之后提出了一个考虑多方式鲁棒稳定约束条件下最大化系统跟踪性能的调速器参数优化方法,避免了切除调速器,保证了系统的跟踪性能。本文提出的方法可以同时对多个机组调速器进行优化,从而无需考虑机组的优化顺序。本文最后通过云南电网算例验证了分析与优化方法的有效性。

1 统一频率模型

超低频振荡具有振荡周期长、振荡频率低的特点。由于时间尺度较大,在分析电网的超低频振荡问题时,可以近似认为那些较快的动态过程已经衰减完全,整个系统以一个共同的频率振荡。基于该思想,文献[18-19]提出并验证了用统一频率模型代替详细模型对超低频振荡现象进行模拟的方法。文献[17]将统一频率模型应用到云南电网超低频振荡分析中,证明了模型应用的可行性。

多机系统统一频率模型如图1所示。图中ΔPmΣ为总机械功率变化量,ΔPeΣ为总负荷变化量,MΣ为系统等效惯性常数,D为负荷阻尼系数。假设调速器的传递函数为G(s),原动机的传递函数为T(s),定义调速器—原动机系统传递函数为：

GT(s)=G(s)T(s)

(1)

则统一频率模型的回路传递函数为：

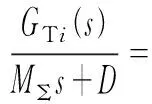
i=1,2,…,Ns+Nh

(2)

式中：Lsubi(s)为各机组的子传递函数;Ns为火电机组数；Nh为水电机组数。可见统一频率模型回路传递函数L(s)可看作各机组子传递函数Lsubi(s)之和。

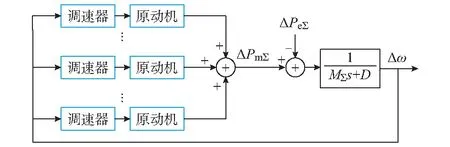
图1 用于研究超低频振荡的统一频率模型Fig.1 Unified frequency model for analysis of ultra-low frequency oscillation

调速器与原动机的模型对超低频振荡问题存在重要的影响。云南电网方式数据中使用的模型可参考文献[20],本文为了分析方便将模型做了合理简化,不会对分析结果造成影响。

水轮机经典模型的传递函数表达式为[6]：

(3)

式中：ΔPm为机械功率变化量;Δy为阀门开度变化量;TW为水流惯性时间常数。水轮机详细模型还需考虑调压室及管道弹性的影响,具体可参考文献[17,21-22]。

调速器通过调节阀门开度y来调整原动机输出功率Pm。如今大部分水电机组采用如附录A图A1(a)所示的比例—积分—微分(PID)型调速器,其传递函数为[22]：

(4)

式中：KP为比例系数;KI为积分系数;KD为微分系数：bp为永态下垂系数：TG为伺服系统时间常数。

虽然云南电网中仍有部分小型水电机组采用如附录A图A1(b)所示的机械液压型调速器,但是其与PID型调速器的结构可以互相转换,两者参数Dd,Td与KP,KI,KD存在如式(5)所示关系[23-24],故本文仅讨论PID型调速器。

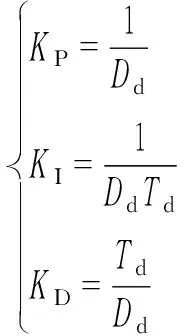
(5)

火电机组的原动机及调速器模型详见附录B。不难发现,与火电机组不同,水电机组原动机传递函数Th(s)不是最小相位的,存在如式(6)所示的RHP零点。原动机传递函数是否存在RHP零点是水电机组与火电机组之间最本质的区别。

(6)

TW的数值与水电厂引水管道长度L成正比。大型水电厂的引水管道长度L很长,故大型水电机组的TW很大,Z很小。在接下来的章节中将证明,Th(s)具有很小的RHP零点Z是造成超低频振荡的关键因素。

2 超低频振荡稳定性分析

本节基于奈奎斯特矢量裕度分析了水电机组与火电机组对超低频振荡稳定性的影响,阐释了造成超低频振荡的关键原因,并分析了负荷的频率调节效应对超低频振荡产生的影响。

2.1 矢量裕度

奈奎斯特曲线距离复平面上(-1,0)点的最小距离能够严格确定系统的实际稳定裕度,即矢量裕度[25-26]。定义矢量VM为复平面上从(-1,0)指向奈奎斯特曲线距离(-1,0)最近点的向量,则其表达式为：

VM=L(jωc)+1

(7)

式中：ωc为系统的振荡频率。显然|VM|即为矢量裕度。

通过判断某台机组对VM的影响可以判断该机组对稳定裕度的影响。根据式(2),统一频率模型回路传递函数L(s)为各机组子传递函数Lsubi(s)之和,因此在超低频问题分析中有

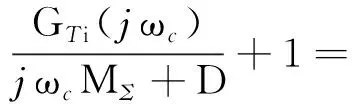
i=1,2,…,Ns+Nh

(8)

式中：VM,subi为各机组的VM分量。

从而判断某台机组对稳定性的影响即为判断该机组对应VM,subi对|VM|的影响：当其方向指向(-1,0)时,该机组使|VM|减小,L(s)的奈奎斯特曲线被拉向(-1,0),机组使系统稳定性恶化;当其方向远离(-1,0)时,该机组使|VM|增大,L(s)的奈奎斯特曲线被拉离(-1,0),机组使系统稳定性改善。

2.2 超低频振荡机理分析

基于所提出的矢量裕度法,本节分析超低频振荡发生的关键原因。假设系统中有Ns台同构同参数的火电机组,Nh台同构同参数的水电机组,则系统回路传递函数L(s)为：

(9)

式中：GTs(s)为火电机组调速器—原动机传递函数;GTh(s)为水电机组调速器—原动机传递函数。

在大网中,系统总惯性MΣ非常大,而D相对较小[3],本节近似忽略D的影响。定义GTh(s)和GTs(s)的频域特性GTh(jω)和GTs(jω)分别为：

(10)

式中：Rh，Rs和Ih，Is分别为实部和虚部。

则火电机组与水电机组在VM中的分量表达式分别为：

(11)

式中：VMs为火电机组相关分量;VMh为水电机组相关分量。

利用火电机组与水电机组Rs(ωc),Is(ωc)和Rh(ωc),Ih(ωc)的性质可以判断VMs和VMh在复平面中的方向,从而确定机组对稳定性的影响。

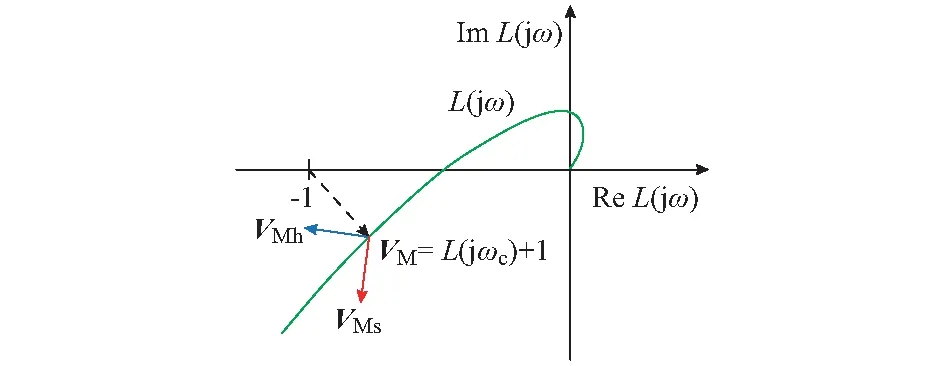
图2 系统矢量裕度Fig.2 Vector margin of system

对于GTs(s),由于其为最小相位传递函数,在振荡频率处GTs(jω)相位略微滞后,位于复平面第四象限,即Rs(ωc)>0,Is(ωc)<0,因此VMs在复平面的方向为左下。对于GTh(s),由于存在RHP零点(式(6)),在超低频段中其相位大幅滞后,若由于调速器参数整定不当导致调速器的滞后相位过大,则此时GTh(jω)在振荡频率处位于复平面第三象限,即Rh(ωc)<0,Ih(ωc)<0。因此在调速器参数整定不当的情况下,VMh在复平面中的方向为左上。

图2显示了指向左下的VMs、指向左上的VMh以及矢量VM。由于统一频率模型回路传递函数L(s)中无RHP极点,故当系统稳定时,L(s)的奈奎斯特曲线不包络(-1,0),VM方向落在复平面第四象限中。显然,火电机组的VMs使奈奎斯特曲线远离(-1,0),增强了系统稳定性,而水电机组的VMh使奈奎斯特曲线靠近(-1,0),恶化了系统稳定性。

综上所述,当保持系统惯性MΣ不变,且增大水电机组数量Nh时(即提高水电渗透率),VM朝左上方移动,回路传递函数奈奎斯特曲线靠近(-1,0),系统稳定裕度下降。水电渗透率过高是使系统出现超低频振荡的主要原因,这是因为水电机组原动机传递函数Th(s)存在RHP零点Z(式(6)),使得GTh(s)在振荡频率处相位滞后过多。RHP零点Z与TW关系密切,大型水电厂机组的TW很大,Z很小,从而GTh(s)滞后相位很大,因此在超低频振荡发生时起负作用的往往是大型水电厂机组,与实际情况相符。

2.3 负荷频率调节效应对稳定性的影响

系统中部分负荷的有功功率随频率变化而改变,即具有负荷频率调节效应。在统一频率模型中,负荷阻尼系数D的物理意义为频率变化1%所引起的负荷变化百分率[6],因此若系统中具有负荷频率调节效应的负荷越多,则D越大。

负荷阻尼系数D对超低频振荡稳定性的影响分析如下。将s=jωc代入式(2),推导得到回路传递在振荡频率ωc处的增益表达式|L(jωc)|为：

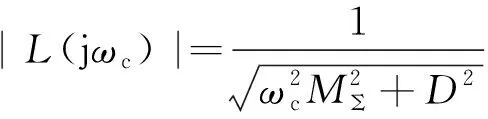
(12)

从式(12)可知,D越大,则回路传递函数在振荡频率处的增益|L(jωc)|越小,回路传递函数奈奎斯特曲线距离(-1,0)的距离越大,系统稳定裕度越大。因此,在系统中增加具有负荷频率调节效应的负荷可以提高系统超低频振荡稳定性。

3 水轮机调速器参数鲁棒优化

从第2节分析的超低频振荡产生机理易知,超低频振荡是由水轮机水锤效应带来的相位滞后引起的。一种简单的解决方案是：当系统实际运行出现超低频振荡现象时,令振荡参与度较大的水电机组退出一次调频。这样做确实能够增强系统的稳定性,然而调速器还需承担跟踪系统频率参考值的任务,让水电机组退出一次调频会使系统的频率跟踪性能下降,降低系统的调频能力。本节对超低频振荡参与度较高的水电机组调速器参数进行优化,以在保证系统稳定性能的前提下,最大化系统的频率跟踪性能。

灵敏度函数的无穷范数是奈奎斯特曲线距离(-1,0)最近距离的倒数,故保证系统稳定性能可通过对灵敏度函数施加约束实现。若要保证多方式系统鲁棒稳定性能,可通过对每个方式的灵敏度函数施加约束实现。

系统的跟踪性能由闭环带宽表示[26]：闭环带宽频率ωB是|S(jω)|自下而上第一次穿越-3 dB时的频率。由其定义可知,增加闭环带宽频率要求降低|S(jω)|的低频增益,而S(jω)=1/(1+L(jω)),故意味着L(jω)的低频增益必须增大。假设系统中有3台机组,即L(s)=(G1(s)T1(s)+G2(s)·T2(s)+G3(s)T3(s))/(Ms+D)。

由于参数优化的对象均为水轮机组,因此在式(4)代入s=jω后,式中T1(s),T2(s),T3(s)在振荡频率范围内的相位大致相同。忽略伺服系统影响,由于系统带宽小于0.05 Hz,故可以近似忽略KDi的影响。由于bp=0.04～0.05,且KIi的取值一般不超过0.5,因此可以近似忽略bpKIi的影响。从而在低频段中有Gi(jω)≈KPi+(KIi)/(jω)(i=1,2,3),故增大各机组的KP或KI均能增加L(jω)的低频增益,从而增大系统闭环带宽。参考文献[27],将优化目标设置为max(KP1KI1+KP2KI2+KP3KI3)。

综上所述,多方式鲁棒PID型调速器参数优化模型为：

max∑KPjKIj

(13)

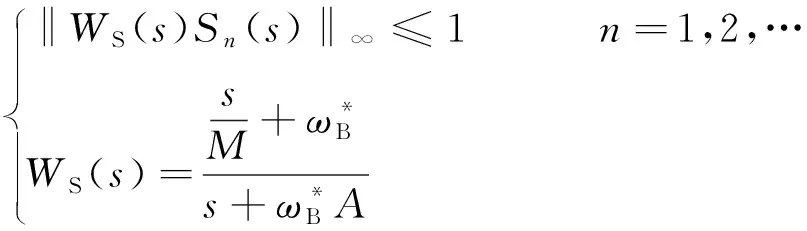
(14)

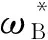
优化模型中加权灵敏度函数无穷范数约束是对加权灵敏度函数幅值在频域上的无穷维约束。注意对超低频振荡问题,约束条件在振荡频率附近可能不满足,而振荡频率的范围大致确定,因此可以在振荡频率附近对加权灵敏度函数幅值扫频,从而将无穷维约束转换为有限维约束。假设扫频频率按升序排列为[ω1,ω2,…,ωN],则多方式鲁棒PID型调速器参数优化模型转换为：

max∑KPjKIj

(15)

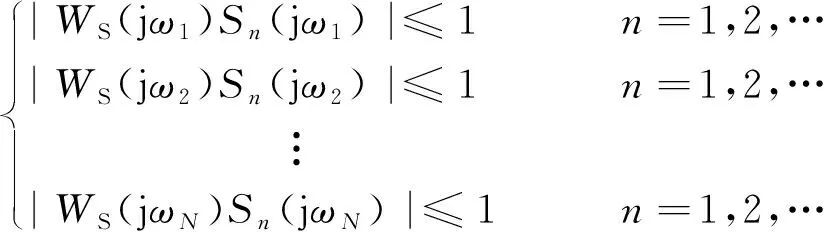
(16)

机械液压型调速器结构可与PID型调速器结构等价,两者参数存在式(5)转换关系,故机械液压型调速器参数优化模型与PID型调速器参数优化模型的区别仅在于将优化目标修改为：

min∑DdjTdj

(17)

4 仿真验证

首先建立南方电网2017年7个方式(冬大、冬小、夏大、夏大极限、夏小、夏小外送、汛期)的统一频率模型,模型的结构与构建过程详见文献[17]。

接下来利用矢量裕度法分析各机组对超低频振荡稳定性的影响。对火电等值机组(GS)、水电等值机组(GH,GM)以及高参与度电厂机组(NZD,LDL,DCS,XW)的原动机—调速器传递函数在关键频率附近(0.05～0.1 Hz)扫频,结果如图3所示。

图3 云南电网发电机组原动机-调速器系统频域特性(ω∈[0.05,0.1]Hz)Fig.3 Frequency characteristics of turbine-governor system for power units in Yunnan Power Grid of China (ω∈[0.05,0.1]Hz)

从图3可知：GS型等值机和GH型等值机在超低频振荡频率范围内的频域特性位于复平面第四象限,其在VM中的分量指向远离(-1,0)方向,增加了稳定裕度;GM型等值机和大部分高参与度电厂机组在超低频振荡频率范围内的频域特性位于复平面第三象限,其VM分量指向靠近(-1,0)方向,减小了稳定裕度;DCS机组在超低频振荡频率范围内的频域特性跨越了复平面第三和第四象限。对于冬大方式,由于系统振荡频率ωc=0.05 Hz,在该频率下DCS机组原动机—调速器系统频域特性GDCS(jωc)=2.065-j7.282,RDCS(ωc)=2.065>0,故DCS机组VM分量指向远离(-1,0)方向,对稳定性起正作用。图4显示了当系统在1.9 s出现1 300 MW功率偏差阶跃时,云南电网冬大方式系统频率仿真曲线与下列情况的差别：①GH总出力PGH增加1 900 MW,GM总出力相应减少;②GM总出力PGM增加600 MW,GS总出力相应减少。仿真结果验证了矢量裕度法的分析结果。

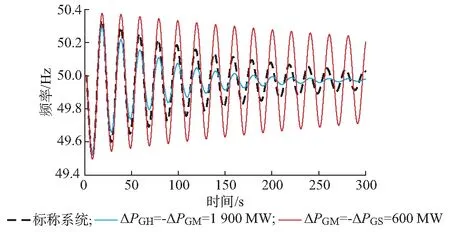
图4 云南电网统一频率模型仿真曲线Fig.4 Simulation results of single-frequency model for Yunnan Power Grid of China

现在分析为何水电机组GH和DCS起正作用。GH是小型水电厂机组的等值机组,其TW相对较小(GH的TW=1.0,GM的TW=3.0),GTGH(jωc)在超低频段内的滞后相位较小,调速器并不需要提供非常大的超前相位就可使其VM分量方向指向远离(-1,0)方向,对稳定性起正作用。对于DCS,忽略伺服系统时间常数TG的影响,将其PID调速器参数(KP=4,KI=0.048,KD=0)与其他水电机组(如GM型等值机组)的PID调速器参数(KP=2.5,KI=0.5,KD=1)代入式(4),可知当ωc=0.05 Hz时,GDCS(jωc)=4.0∠-1.84°,而GGM(jωc)=2.8∠-23.44°,GDCS(jωc)比GGM(jωc)多提供21.6°超前相角,使其VM分量指向远离(-1,0)方向,对稳定性起正作用。DCS机组起正作用的原因为其调速器参数整定较好。

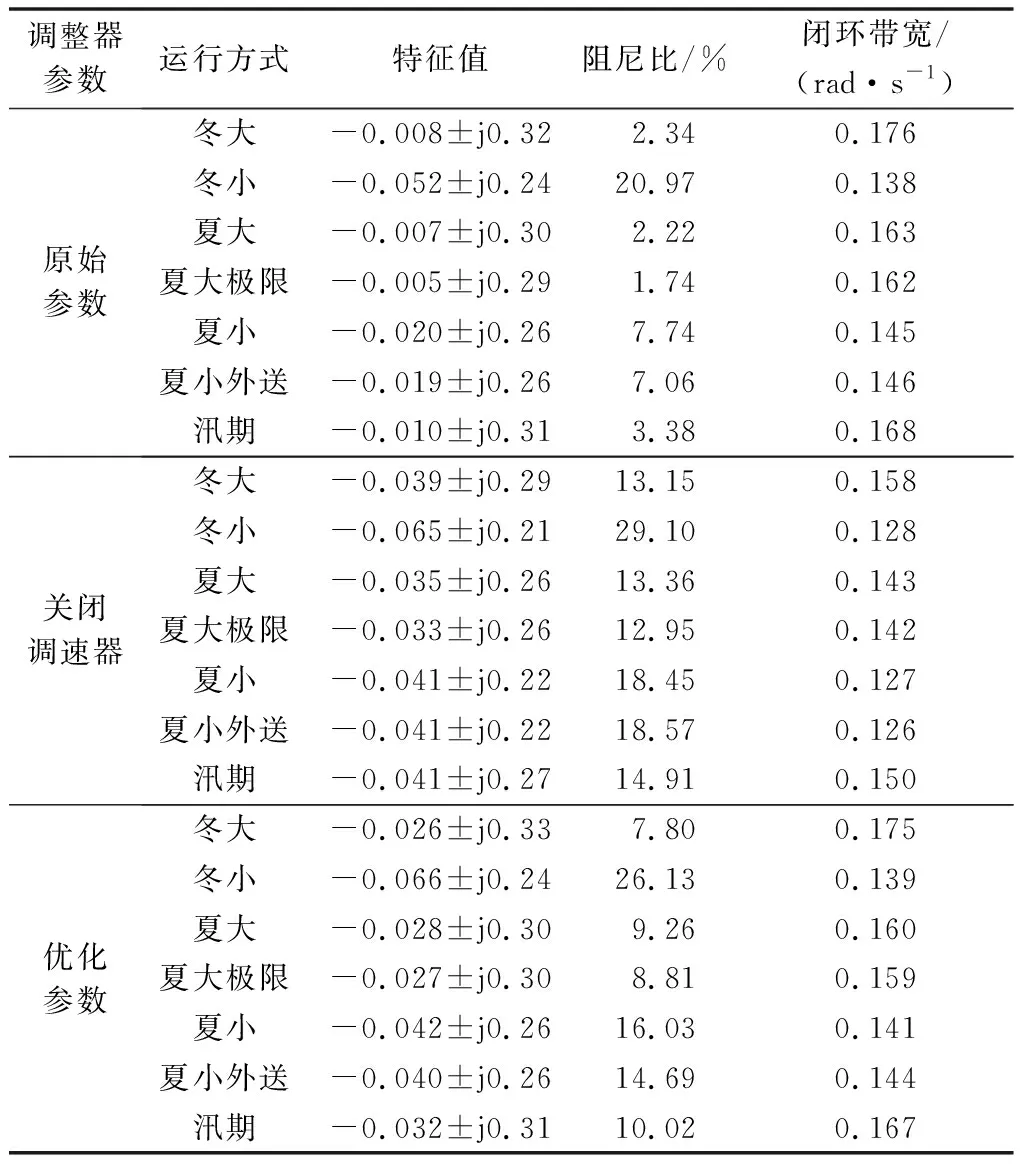
表1 云南电网主导特征值与闭环带宽频率Table 1 Dominant eigenvalue and closed-loop bandwidth frequency of Yunnan Power Grid of China

5 结语

本文基于奈奎斯特矢量裕度对多机电力系统超低频振荡问题进行了机理分析,分析结果具有普遍意义。分析结果表明,由于水电机组存在RHP零点导致的水电机组原动机传递函数相位在振荡频率附近大幅滞后是使系统出现超低频振荡的主要原因。本文还提出了一个考虑多方式鲁棒稳定约束条件下最大化系统跟踪性能的调速器参数优化方法,在满足多个方式稳定裕度的同时对多个机组调速器参数进行了优化。

本文提出的分析与优化方法有效性通过云南电网算例得到了验证,然而所提出的优化模型中约束维度会随着运行方式数量增多而线性增长,给计算最优解带来困难。如何设计满足大量运行方式鲁棒性能要求的调速器参数还需进一步研究。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。