含电压源换流器的交直流混联电网状态估计快速解耦法
张 潼, 王 毅,2, 翟明玉,2, 黄 煜, 赵凌骏
(1. 南瑞集团(国网电力科学研究院)有限公司, 江苏省南京市 211106;2. 智能电网保护和运行控制国家重点实验室, 江苏省南京市 211106;3. 东南大学电气工程学院, 江苏省南京市 210096)
0 引言
多端柔性直流(voltage source converter based multi-terminal direct current,VSC-MTDC)输电技术已成为解决分布式可再生能源并网及消纳问题的有效技术手段[1-2]。这一新型复杂的交直流混联输电结构对调度系统的发展提出了新的需求。交直流状态估计作为能量管理系统(energy management system,EMS)的数据服务模块,为交直流系统的潮流计算、在线安全分析等高级应用提供了反映网络运行状态的实时数据断面,是数据系统的质量及可靠性保证[3-4]。
常规高压直流局限于两端口、点对点直流输电,不适合扩展为直流电网。针对这一常规交直流系统,国内外学者提出的状态估计算法主要分为同时求解法[5-6]和交替迭代法[7-9]两类。文献[5-6]将交流、直流量测方程联立,建立统一的估计计算模型,在迭代过程中同时修正交流、直流状态变量,严格保留了交、直流变量间的耦合关系,具有计算模型直观、数值收敛性好的优点,但该方法难以有效继承原有的交流状态估计程序。交替迭代法的求解思想则是对直流、交流系统顺序迭代求解,其交流部分对状态估计程序的沿用性好、实现方便,因此得到更多的研究及关注。为了解决交替求解引入的交接误差和整体收敛性问题,文献[7-9]从数学变换的角度提出了一些改进的交直流分解策略。文献[10]结合电压源换流器(voltage source converter,VSC)的稳态特性,通过同时求解法对含两端电压源换流器型高压直流(VSC-HVDC)的系统进行了状态估计;文献[11]在此基础上利用高斯消元思想将信息矩阵分解为交、直流两部分,每次迭代重新形成统一的交直流雅可比矩阵,在本质上属于同时求解思想的改进算法。
随着直流规模、交直流量测量大幅增加,迫切需要发展交直流系统通用、高效的状态估计模型和算法。本文提出了一种交直流快速解耦状态估计算法,充分利用交直流系统的稳态物理特性,在计及交流、多端柔性直流子系统之间耦合关系的基础上,忽略雅可比矩阵中的某些次要因素,实现交直流系统有功、无功的解耦交替计算。
1 AC/DC模型和量测系统
1.1 交直流系统描述
VSC作为直流与交流网络之间功率交换的纽带,是交直流系统的关键控制元件。稳态运行时忽略换流器谐波分量,可以得到图1所示的第i个换流站的单相等效电路。图中,Us,i为交流母线公共连接点(PCC)的电压幅值,交流母线经过滤波器Xf,i、换流电抗器Xl,i连接到换流桥和直流母线。
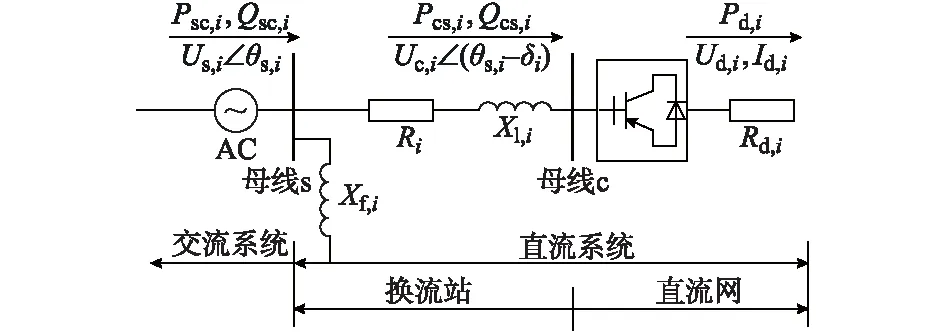
图1 单相VSC稳态物理模型Fig.1 Steady-state physical model of single-phase VSC
考虑换流站稳态外特性,VSC可以采用两电平、三电平中点钳位或模块化多电平换流器(MMC)结构,MMC的换相电抗通过其桥臂电抗Xarm,i计算得出[12]。母线c位于换流电抗后,Uc,i为VSC的输出基波电压幅值;δi为脉宽调制(PWM)相位角,表示交流系统电压与调制波之间的相位差。基于双边傅里叶级数调制理论,VSC输出的交流线电压Uc,i为:
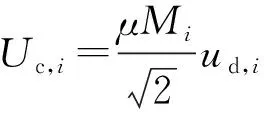
(1)
式中:μ为由脉宽调制方式确定的常数;Mi为脉宽调制比;ud,i为换流器直流侧的极间电压。
脉宽调制比Mi和移相角δi是VSC的控制量,当对VSC进行调制时,调节Mi和δi可实现对交换功率的控制。
1.2 拓展后的交流量测方程
考虑交直流系统中的交流母线数为nac,直流母线数为ndc,交流网与直流网通过nc个VSC连接。交流网中不与换流器连接的nac-nc个节点记作集合N,与换流器相连的边界节点记作集合L。交流量测模型包括注入功率量测、线路功率量测以及母线电压量测。边界集合L的注入量测方程如下:
(2)
(3)
式中:i∈L;Ui为交流节点电压幅值;θij为节点i和j间的相角差;Gij和Bij为节点i和j间的电导和电纳;下标j表示与节点i直接相连的节点,用j∈i表示。
1.3 多端柔性直流量测方程
由图1所示,直流系统可分为VSC连接支路和直流网络两部分。直流模型可相应地分为直流量测、计及损耗的注入量测及VSC控制伪量测。
直流系统各物理量的参考方向见图1,选择直流电压ud,i和VSC输出电压幅值Uc,i,移相角δi作为状态变量,其余物理量Psc,i,Qsc,i,Pcs,i,Qcs,i,Pd,i,Mi,Id,i可由状态量推算得出。
1)直流量测

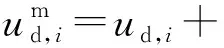
(4)

(5)
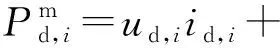
(6)

(7)
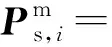
Ps,i(Uc,i,δi,Us,i,Yi,αi)+ηPs,i
(8)
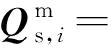
Qs,i(Uc,i,δi,Us,i,Yi,αi)+ηQs,i
(9)
其中,式(4)和式(5)为VSC直流电压、直流电流注入量测;式(6)和式(7)则为直流网络的注入功率量测以及支路量测,Gd=(gd,ij)为直流网络电导矩阵;式(8)和式(9)为VSC支路的交直流交换功率量测,量测方程见附录A式(A1)和式(A2)。
2)计及损耗的注入量测
考虑直流系统的功率平衡关系,为简化计算,VSC工作损耗经常忽略不计,此时有直流功率Pd,i与换流桥直流侧的有功功率Pcs,i相等。然而对计算精度有较高要求时,换流开关器件的损耗不可忽略[13]。描述功率约束的注入方程计及了VSC的功率损耗,表示为:
0=ud,iid,i-Pcs,i(Uc,i,δi,Us,i,Yi,αi)+Ploss=
ud,iid,i-Pcs,i(Uc,i,δi,Us,i,Yi,αi)+
(10)
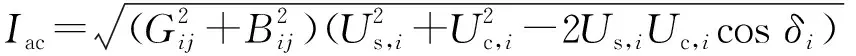
3)VSC控制伪量测方程
多端直流系统运行灵活,但控制策略更为复杂。由于状态估计中考虑某个时间断面,系统级控制方式可以看作各个换流器的基本控制方式的组合。VSC有功类和无功类的控制伪量测方程分别如式(11)和式(12)所示。
(11)
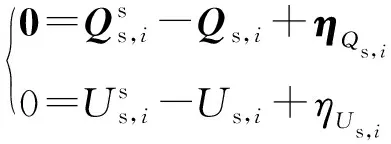
(12)
式(11)为有功类的定直流电压、定交流有功功率控制;式(12)为无功类的定交流母线电压、定交流无功功率控制。每台VSC各含有1个有功和无功控制伪量测方程。
2 交直流状态估计模型及解耦策略
2.1 交直流状态估计模型
综上所述,AC/DC状态估计的非线性量测方程由式(3)—式(12)组成,可统一表达为:
(13)

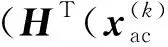
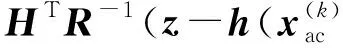
(14)
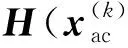

(15)
式(14)、式(15)构成同时求解法状态估计的数学模型。这种方法严格计及了交、直流之间的耦合因素,可以看作其他交直流状态估计模型的基础,具有重要的理论意义。
为方便表述,将部分交流量测扩展至直流部分,并按有功、无功类对交直流量测分类,修改后的分块AC/DC量测如下。
1)不与VSC连接的交流内部节点集合N的无功功率和电压幅值量测zQ。
2)交流内部节点集合N的有功量测zP。
3)直流网电压、有功量测,包括式(4)—式(7),记作zD。
4)交流边界节点集合L的有功量测以及VSC支路有功量测和零注入量测,包含式(3)、式(8)和式(10),记作zPd。
5) 交流边界节点集合L的无功量测以及VSC支路无功量测,包括式(3)和式(9),记作zQd。
将式(11)和式(12)按照控制类型归入以上量测,则式(15)中的AC/DC雅可比矩阵可以按照式(16)中的分块形式构建。
θUudUcδ
(16)
式中:“×”代表非零子阵,“0”代表零子阵。
2.2 解耦策略
观察式(16),AC/DC雅可比矩阵存在较多零子阵,但是各非零块构成了连通图,所以无法解耦计算。因此,考虑从混联系统稳态特性出发,忽略雅可比矩阵中的某些次要因素,打开连通图实现交直流解耦运算。
首先,考虑HPd-Uc子矩阵,矩阵下标Pd-Uc表示∂zPd/∂Uc,矩阵元素为交直流有功交换功率对VSC输出电压幅值的偏导数,表示为:
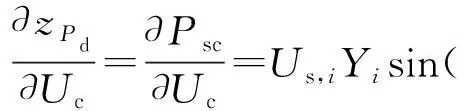
(17)
式中:Yi和αi为常数,其中αi=arctan(Ri/Xl,i)。由于线路电阻远小于线路电抗,αi数值接近于0。
记系数k=Us,iYi,式(17)可以改写为:
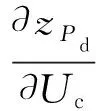
(18)
将式(17)与HQd-Uc子矩阵元素进行纵向对比,HQd-Uc为交直流无功交换功率对VSC输出电压幅值的偏导数。其中,δi是第i个VSC支路交流母线s与母线c之间的相位差,可以认为δi取值较小。柔性直流工程中的换流电抗器Xl,i、换流阀电容等主回路参数在进行参数设计时需要考虑系统要求的运行功率范围、电压水平和主要控制策略[15]。其中换流电抗器Xl,i取值越小,系统无功损耗越小,跟踪速度越快。然而,考虑到换流器抵御交流系统负序电压的能力,Xl,i的最小取值存在限制。考虑电网背景基波负序电压限制为额定电压的1.5%,为了使VSC能够长期运行,要求流过换流电抗器Xl,i的负序电流不大于VSC额定电流的5%~10%[16],此时有Xl,min=0.5sin(2δi,max)∈[0.15,0.29](标幺值),移相角δi,max的最大值范围为δi,max∈[8.6°,17.4°],此时有

Planning Radar Sites and Configuration of VTS with LINGO Modeling
(19)
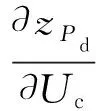
(20)
进一步将式(17)与HPd-δ横向对比,有
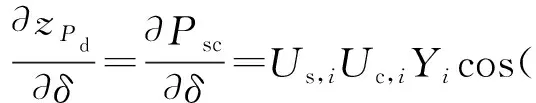
(21)
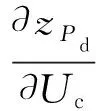
(22)
由式(20)和式(22)可以看出,HPd-Uc子矩阵元素较小,可以选择将其忽略。
其次,对HQd-δ进行分析,得到如式(23)所示的关系,因此也可以解耦处理。

(23)
根据以上分析,交直流雅可比矩阵中的HPd-Uc和HQd-δ子矩阵可以解耦简化。同时,高压交流系统中有∂P/∂U和∂Q/∂θ项接近于0。在此基础上,将交直流量测向量按有功、无功类排列,同时忽略以上元素,则式(16)中的雅可比矩阵表示为:
θudδUUc
(24)
至此得到了如式(24)所示的分块对角形式的交直流量测雅可比矩阵。代入式(14)中的状态估计迭代形式,可以实现交直流混联系统的有功、无功解耦迭代计算:
(25)
含VSC-MTDC的交直流系统状态估计的解耦策略具有以下特点。
1)正常运行条件下,有功功率与调制比、无功功率和直流电压及相角之间耦合关系较弱,反映在雅可比矩阵中HPd-Uc,HQd-δ,HQd-ud元素数值较小,因此可以将ud,δ,Uc分别与交流变量合并解耦。
2)解耦处理后,由于HPd-θ和HQd-U矩阵保留了交直流系统之间的耦合关系,因此不需要增加外循环,可以直接同时对交、直流状态变量迭代更新,不会存在引入交接误差以及收敛性的问题。
2.3 常数化
交直流系统稳态运行时,网络状态在正常工况附近变化平缓,因此可以在实现解耦的基础上,对雅可比矩阵常数化处理,加快迭代修正速度。
交流系统中,状态变量的初始值通过设定值给定,即认为节点电压接近参考电压且支路相角差很小,采用:
(26)
式中:Uref为交流电压正常运行参考值。
类似的,直流系统的状态变量也可由式(27)进行常数化处理。
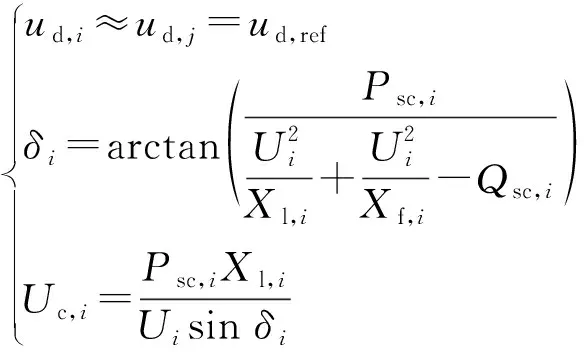
(27)
式中:ud,ref为换流器直流侧的极间电压的正常运行参考值;Psc,i和Qsc,i由换流器的控制值或可信量测值给定。雅可比矩阵中的非零元成为常数值,在系统结构和量测不变的条件下,状态估计只需进行一次因子分解,在大型系统的应用中可以提高实时估计速度。
3 交直流状态估计算法实现
在第2节解耦策略的处理下,含VSC-MTDC的交直流混联系统可以实现改进的快速解耦状态估计计算,算法的具体实现步骤如下。
步骤1:读入交直流算例数据,根据支路信息构建交流导纳矩阵Y,直流电导矩阵Gd以及换流器支路相关阻抗矩阵Zc;根据VSC控制方式设定控制类型值。
步骤2:量测采样,读入交直流量测信息,结合换流器控制类型,对混合量测顺序优化分类,形成扩展的有功、无功混合量测向量。
步骤3:状态估计初始化,根据式(26)和式(27)对扩展的交直流变量赋初值;针对新的量测向量和状态变量分别计算有功量测雅可比矩阵HP(xP)和无功量测雅可比矩阵HQ(xQ),并计算信息矩阵GP和GQ。
步骤4:设置迭代计数器k和有功、无功迭代收敛标志KP和KQ,初始值设置为1表示未收敛。利用状态估计迭代修正式(14)进行有功状态估计∂zp/∂xP迭代,有功收敛则令KP=0并转去无功计算;进行无功状态估计∂zq/∂xQ迭代,无功收敛则令KQ=0并转到有功计算。
步骤5:判断∂zp/∂xP和∂zq/∂xQ迭代是否同时满足收敛条件,若同时收敛则输出结果;否则,返回步骤4进行下一次迭代。
4 算例验证
为验证本文提出的含VSC-MTDC的交直流快速解耦状态估计算法的正确性及有效性,对修改的含3端柔性直流的IEEE 14和IEEE 118节点交直流系统算例进行了MATLAB仿真计算。仿真中,交直流模拟量测系统以潮流计算的结果为真值,并在此基础上构造满足正态分布的随机量测误差。混联系统的量测规模见附录A表A1。
为了保证结果的可比较性,交直流状态估计算法采用同一个模拟量测系统,收敛精度均设置为10-5。不失一般性,对20次量测采样进行估计计算,以式(28)中的统计值为性能指标验证状态估计滤波性能。根据文献[4],量测误差统计值SM≈1说明量测系统符合要求;估计误差统计值SB<1,目标函数统计值J接近量测冗余度,表明算法的滤波效果良好。
(28)
式中:T为采样总数;m为量测总数;zi,t和hi,t(x)分别为第i个量测t次采样的量测值和估计值;σi为第i个量测的标准差;Si为第i个量测的潮流真值。
4.1 估计质量
采用修改的IEEE 14节点测试算例,VSC分别连接于交流节点12,13,14,形成一个3端口环形连接的柔性直流系统。测试系统拓扑结构图见附录A图A1,直流系统参数见附录A表A2和表A3。设置VSC的Xl,i=0.29(标幺值),选择VSC2的移相角δi为最大值时的潮流断面进行算例验证,VSC的控制方式及控制目标如表1所示,其中各数值均为标幺值。

表1 多端直流系统控制方式Table 1 Control modes of MTDC system
本文方法与同时求解法的状态估计结果及其精度比较见表2至表4。其中,表2和表3分别为直流部分变量估计结果和交直流状态估计统计结果;表4选取了量测模型中具有代表性的交直流交换功率,给出了其平均量测和平均估计误差以进一步说明算法的滤波性能。

表2 直流状态估计统计结果Table 2 Statistical results of DC state estimation
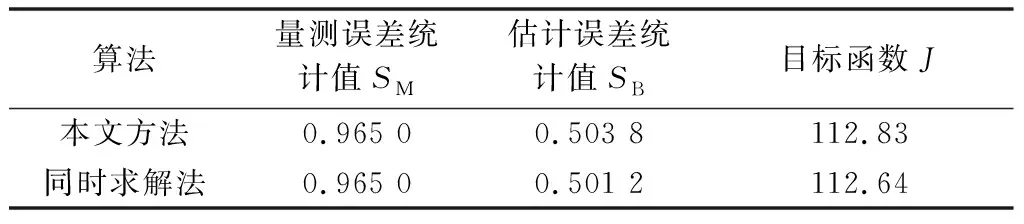
表3 交直流状态估计统计结果Table 3 Statistical results of AC/DC state estimation
由表2和表3可见,在相同的收敛精度下,本文算法与同时求解法的估计结果相近,并且与状态真值基本一致;其中目标函数统计值J接近系统量测冗余,并且SB 表4中进一步将本文估计结果与交替迭代法[7]对比,以考察混联系统中交直流交换功率量测Psc和Qsc的估计质量。由表4的计算结果可见,本文算法与同时求解法的Psc和Qsc量测的平均估计误差相近,而交替迭代法在VSC交换功率Psc,1和Qsc,3处的估计误差明显偏大。这是由于交替迭代法在交、直流估计子循环中将耦合变量作常数处理,仅在估计外循环中修正状态变量,存在引入一定功率交接误差的问题;同时求解法状态估计没有做简化假设,在迭代过程中严格计及了交、直流之间的耦合关系,因此可以保证混联系统连接处的功率估计精度。本文所提快速解耦法的估计误差与同时求解法相近,在解耦过程中保留了混联系统的耦合关系,避免了交替迭代引入的交接误差,能够保证与同时求解相一致的估计精度。 表4 部分交直流量测的估计误差Table 4 Estimation error of AC/DC measurement 表5对比了本文方法和同时求解法状态估计程序在IEEE14和IEEE118节点算例下的迭代次数和计算时间。在规模较大的IEEE118节点算例中,快速解耦状态估计算法的计算用时由同时求解法的0.64s降低到0.20s,计算效率提高了68%。快速解耦状态估计算法在迭代中采用恒定的交直流雅可比矩阵,不需重复进行因子分解运算,减少了计算量和运行时间,仅以增加少量的迭代次数为代价。本文算法具有保证估计精度并提高实时计算效率的优势。可以预计,随着系统规模增加,本文算法在计算速度方面具有优势,适宜在交直流特大规模电网中的应用。 表5 运算时间统计结果Table 5 Statistical results of calculating time 估计精度和计算效率是用以衡量状态估计软件在线应用性能的两个重要因素,为了协调兼顾AC/DC状态估计的估计精度以及计算速度,本文提出了一种适用于含多端柔性直流的交直流快速解耦状态估计算法。本文所提算法的滤波性能良好,可以保证与同时求解法一致的估计精度,并且提高了实时计算速度,在大电网适用性方面更具优势,同时,本文所提方法可以基于传统交流网络PQ解耦法扩展,在功能实现上更为方便。 本文方法侧重于含VSC的交直流估计算法研究,为了满足实际工程应用的要求,对于交直流混联电网的状态估计还有应用化问题需要解决,笔者在后续研究中会进一步考虑AC/DC混联系统的不良数据辨识以及直流量测权重的合理设置。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。
4.2 计算速度

5 结语

