基于实物期权的增量配电网投资决策

叶 彬， 刘敦楠, 杨 娜， 刘明光， 赵宁宁， 王 宝

(1. 国网安徽省电力有限公司经济技术研究院， 安徽省合肥市 230022； 2. 新能源电力系统国家重点实验室(华北电力大学)， 北京市 102206)

0 引言

增量配电网放开是本次电力体制改革的主要任务之一，其目的是在配售电侧引入竞争，同时推动售电市场[1]。2016年10月发布了《有序放开配电网业务管理办法》，之后在各省针对增量配电网进行了布点，在第一批中确定了延庆智能配电网等105个增量配电网项目[2]。在增量配电网投资过程中，其投资决策既需要考虑当前电力体制改革的不确定性、收益来源的特殊性等情况，同时又需要更加强调电网投资的盈利性。由于增量配电网自负盈亏，对于电网公司及社会资本而言，增量配电网投资将带有极大的不确定性[3]。

现有配电网投资决策的研究思路可以分为综合评价、投资决策判别指标两种[4]。在综合评价方面，各研究学者通过构建不同的指标体系，采用不同的综合评价方法，提出了针对不同情况的投资项目评价方法[5-7]。采用综合评价方法具有评价全面的优点，但也难以避免会出现难以量化、评判较为主观等问题。常用的投资决策判别指标为财务指标，主要通过完善测算思路及测算流程，对传统投资决策方法进行了改进[8]。传统投资决策方法难以考虑不确定性情况下的风险投资，对于投资价值评估不够全面。

实物期权理论由金融期权定价理论衍生而来，在不确定性投资决策中得到了广泛应用[9]。其应用范围包含具有较强不确定性的投资活动、价值评估等方面[10]。实物期权在电力行业中的应用主要集中在可再生能源发电方面，尤其针对风电投资进行了大量研究[11]。研究表明，引入实物期权方法可以优化决策、选择有价值的优质项目，为风电项目的投资决策者提供新的投资决策思路[11-12]。然而，基于实物期权理论针对电网投资决策理论的研究较少。有学者指出，采用实物期权对电力投资决策进行分析，是对传统投资决策判别指标的补充[13]。文献[14-15]引入了实物期权法，对实物期权方法在电力投资中的应用及参数取值进行了研究。文献[16-17]结合传统净现值法存在的问题，运用实物期权方法提出了相应的投资决策分析方法。结合实物期权的电网投资决策分析方法已经取得初步成果，但仍存在两方面不足：一是目前针对增量配电网投资面临的不确定性尚未进行研究；二是并未结合电网投资特性，研究实物期权模型中关键参数波动率的测算方法。

综上所述，本文基于上述研究成果，针对增量配电网投资特性，分析其盈利模式，在此基础上分析其收益影响因素，构建了增量配电网Black-Scholes投资决策模型(简称B-S模型);然后基于增量配电网投资的特点，构建了模型关键参数期权波动率测算模型;最后通过算例验证了模型有效性，为新形势下增量配电网投资决策提供了借鉴。

1 增量配电网投资盈利模式分析

增量配电网理想盈利模式包括供电服务盈利和售电服务盈利两个部分，其中供电服务盈利可以分为三个方面：配电服务费、相关增值服务收入，以及参与辅助服务市场收入。

现阶段，配电服务费将作为增量配电网公司供电服务的主要营收来源，同时《有序放开配电网业务管理办法》指出：增量配电区域的配电价格暂按售电公司或电力用户接入电压等级对应的省级电网共用网络输配电价扣减该配电网接入电压等级对应的省级电网共用网络输配电价执行。从购售电量的角度来看，投资增量配电网的单位电量收益是低电压等级与高电压等级之间存在的输配电价价差。根据中国已公布的输配电价，梳理不同情形下的输配电价价差，结果见附录A表A1。

从目前输配电价核算施行的情况来看，输配电价价差主要包括110 kV与10 kV之间和220 kV与10 kV之间两种。110 kV与10 kV之间价差平均值为0.069 2元/(kW·h)，价差最大值为0.170 9元/(kW·h)；220 kV与10 kV之间价差平均值为0.085 1元/(kW·h)，价差最大值为0.190 9元/(kW·h)。

从输配电价核算省份来看，输配电价价差较大的地区为广西、深圳、贵州、云南，蒙西、宁夏、湖南次之，安徽、湖北、河北、冀北、北京最小。因此，从地域选择来看，广西、深圳、贵州增量配电网投资价值最大。

从输配电价价差来看，110 kV与10 kV之间的价差均小于220 kV与10 kV之间的价差，这是由于220 kV与10 kV之间需要更多的配电网投资。两种模式的价差在0.005～0.030元/(kW·h)之间。

2 增量配电网投资不确定性分析

在原有的电力系统运行方式下，电网拥有输配电网的建设、维护、运营权。在新电力体制改革要求下，将未来新建配电网确定为增量配电网，并且划定范围，允许民间资本参与竞争。增量配电网放开的目的是将输配电分开，将电网公司置于市场竞争之中，这也是中国电力市场化改革的关键步骤。同时，将各增量配电网与原有电网设施分开，形成增量配电网单独核算，并且在一定程度上自负盈亏。在这种情况下，在运营及收益方面存在诸多不确定性，主要有以下几个方面。

1)负荷、电量的增长波动性。增量配电网运营的大部分收益来源于电力供应，该部分收益一方面取决于输配电价，另一方面与负荷及电量有关。在未来一段时间，输配电价在政府管制下，将基本保持稳定，不会有大的波动。电量的波动性将会对增量配电网运营收益产生影响，进而影响其投资价值，并决定增量配电网期权价值。影响用电量的因素有很多，主要包括经济发展情况、产业结构、行业前景、气候、能源替代情况等。

2)不同建设方案引起的不确定性。在电网规划过程中，可以通过不同的电网建设方案满足未来用户负荷。不同的建设方案在线路架构、变电数量方面会存在较大差别，同时针对不同类型的用户，采用的材料设备的成本亦有不同。因此，不同的建设方案在项目投资成本方面存在差异。项目投资成本具有不确定性，从而导致增量配电网收益的不确定性。同时，技术进步同样会影响电网建设方案，从而影响投资成本。

3)电网投资项目刺激作用引起的不确定性。电网投资建设在用于满足现有电力用户需求的同时，也会产生正向刺激作用。尤其对于工业园区而言，各工业企业对于电能供应质量及安全的保障要求较高，园区内完备的电网设施建设将为招商引资提供便利，从而吸引企业入驻园区。配电网质量及建设周期的长短在其中具有至关重要的作用。

4)运营模式不同引起的不确定性。未来的电力系统将不再独立，尤其对于具有多种能源需求的企业来说，综合能源服务能更好地满足用户需求。因此，未来的增量配电网的含义也不仅仅是电网，还应包括用于供冷、供热的管道。在这一背景下，增量配电网多种能源协调供应显得十分必要，而多种能源互补协调优化调度的方式，使得增量配电网收益存在不确定性。

3 增量配电网投资实物期权估值模型

3.1 实物期权理论适用性分析

对配电网进行投资并非一蹴而就，而是一项经过研究后做出的科学的投资活动。配电网投资可以分为以下几个阶段：可行性研究阶段、建设期、运营期。这与在金融市场中的期权交易类似，期权的购买实际上就是阶段性购买某项标的资产。第一阶段是购买标的资产的期权；第二阶段是购买标的资产。配电网投资成本较大，一旦进行建设，将不可撤销，因而具有不可逆性。

配电网投资不仅在投资时间方面具有灵活性，同时在投资方案的选择方面也具备灵活性。投资者可以选择投资时机，也可以自己制定投资方案，控制投资过程，对建设期长短进行控制。这一情况与金融期权类似，期权购买者具有自主权，可以灵活处置期权资产。

在新形势下，增量配电网在运营过程中存在许多不确定性。根据风险投资理论，投资过程中不确定性越大，意味着投资项目估值也应越大[18]。在传统投资决策模型中无法对不确定性进行测算，因而在一定程度上不能完全估计增量配电网投资项目价值。而期权的本质就是不确定性，因为不确定性和风险的存在才使得金融期权依托实物资产而存在。

综上所述，在本文研究过程中采用实物期权方法可行。

3.2 实物期权估值模型

增量配电网投资过程具有多阶段属性，从投资时序来看，增量配电网投资过程可分为增量配电网运营权获得、电网新建或增容等阶段。

其中，电网新建或增容包含多个阶段，电网投资需要依据用电需求进行。获得配电网运营权之后，增量配电网投资具有看涨期权特性。同时，电网投资时间可以通过用电需求增长确定，具有欧式期权特性。因此，增量配电网投资具有欧式看涨期权的特性。本文主要研究两阶段投资过程，即电网新建或增容等阶段只考虑一次投资。在此选取针对欧式看涨期权的B-S模型进行投资期权价值评估。模型公式如下：

C0=S0N(d1)-Xe-rTN(d2)

(1)

其中

(2)

(3)

式中：C0为增量配电网投资期权价值；S0为增量配电网净现金流入；N(·)为累计正态分布函数；X为增量配电网投资额；r为无风险利率；T为增量配电网投资期限；σ为增量配电网收益波动率。

设增量配电网投资总价值为V，净现值为VNPV，则有

V=VNPV+C0

(4)

由上式可以看出，在引入实物期权理论后，增量配电网投资价值除净现值估值之外，还考虑了不确定性带来的期权价值，有利于综合考虑投资价值。

3.3 模型参数确定方法

在实物期权模型中，主要包含以下参数：标的资产的现值及其波动率、无风险收益率、有效期限和执行价格等。

1)标的资产的现值：指增量配电网建成之后带来的现金流现值。需要对项目生命周期内的现金流进行预测，然后选取合理折现率对现金流折现，即可得到标的资产的现值，其中不包括建设期投入。

2)标的资产波动率：指预期收益波动的标准差。受能源消耗量(包括冷热电等多种能源)及能源价格波动综合影响，具体测算过程中将两者分离，依据历史波动率进行参数设定。

3)有效期限：指阶段或建设期长度，在增量配电网投资过程中指投资等待时间。

4)执行价格：指项目投资成本，包括增量配电网设备费、安装费等，根据具体项目进行核算。

5)无风险收益率：指在投资过程中市场的无风险利率。一般选取5年期国债利率作为无风险收益率。

上述参数中，波动率是表示投资项目不确定性的重要因素，也是实物期权模型中的关键参数。下文将针对增量配电网不确定性因素构建收益波动率测算模型。

4 增量配电网投资收益波动率测算方法

标的资产价值波动率是进行实物期权估值时的重要指标，波动率测算的合理性将直接影响价值评估的准确性。目前常用的实物期权波动率测算方法主要有历史值估计、同类型投资活动参考及蒙特卡洛模拟等[19]。由于增量配电网投资刚刚起步，数据积累不足，使得上述方法在实际操作过程中存在困难。因此，本文针对增量配电网投资活动特性，构建了增量配电网投资收益波动率测算模型。

典型园区配电网投资收益受多方面因素的影响。从现阶段电网投资现状来看，电网投资收益仍然来源于输配电业务，因此电网收益主要受输配电量及输配电价的影响。在此构建基于横向对比分析的波动率测算模型。横向对比分析是指同类型园区在同一时间节点上收益的不同，也就是用电量增长情况的不同。

4.1 园区类型判别指标体系构建

园区特征指标有很多，从园区体量大小、所处发展阶段及园区主要电力用户3个维度，选取园区规划面积相对比、园区建成规划比、园区主导行业、园区主要负荷类型4个指标进行园区类型判别。各指标含义及取值方法如表1所示。

在实际测算过程中，可针对上述4个指标对所有园区进行收资，并根据确定的典型园区对各园区指标进行赋值，为相似程度的判别奠定基础。

需要说明的是，在此构建的园区类型判别指标仅是通过园区基本特征进行判别，通过该指标体系筛选之后的园区，在园区发展阶段上并不相同。即选取出的同类型园区将处于不同的发展阶段，从而表征处于不同发展阶段时该类型园区的发展状况。因此，本文构建的基于横向对比分析的波动率测算模型，在一定程度上考虑了园区未来发展的不确定性。

表1 园区类型判别指标体系Table 1 Type discriminant index system for industrial park

4.2 园区类型相似度判别方法选取

在园区类型相似度判别过程中，已经确定了园区类型的一种模式，即项目研究选取的典型园区。因此，在此进行的相似度判别是一种模式识别，即通过一定的定量化方法，将那些和典型园区代表的标准模式相近的园区识别出来。借鉴模糊数学模式识别的方法，通过测算待识别对象和标准模式之间的模糊贴近度[20]，来判断园区之间的相似程度，从而识别出相似园区，为波动率测算奠定基础。

由园区类型判别指标体系可以得到各园区特征量化值，将其特征值进行向量表示，即可得到其园区特征向量。其中，对于选定的典型园区，将其特征向量定义为标准模式，计作A0，则A0=[x01,x02,x03,x04]，其中，x01为规划面积相对比，x02为建成规划比，x03为主导行业，x04为主要负荷类型。同理，针对其余n个待识别园区，同样可以得到其特征向量Ai=[xi1,xi2,xi3,xi4],i=1,2,…，n。

在特征向量构建的基础上，选取模糊模式识别中贴近度的计算方法，选择最大最小贴近度对园区特征向量进行测算，测算得出待识别园区与典型园区之间的贴近度。计算公式如下：

(5)

式中：N(A0,Ai)为A0与Ai的贴近度；∧为取小算子，∨为取大算子。

通过上式即可得到n个贴近度测算值，通过对贴近度进行排序，即可得到与选取的典型园区相似的园区类型。在贴近度测算之后，需要确定园区相似程度的标准，从而从n个园区中筛选出相似园区。选取原则有两种：一是阈值原则，也就是其相近度大于某阈值时，才能判定其为同类型园区，在此将该阈值定义为80%；另一种是择近原则，也就是根据贴近度进行排序，判定贴近度最大的一组园区作为同类型园区，为使得波动率测算可行，在此选取贴近度最大的前20%的园区进行波动率测算。

4.3 同类型园区配电网投资收益波动率测算

在同类型园区横向对比测算配电网投资收益波动率时，由于各园区的配电网投资支出数据获取存在很大困难，在此采用各园区用电量波动率进行代替。通过前述分析可知，在现阶段园区用电量是影响配电网投资收益的主要因素[3]。因此，采用园区用电量波动率代替配电网投资收益波动率具有合理性。

假设从n个园区中选出m个同类型园区，这些园区与选取的典型园区共同构成m+1个同类型园区。选取第t年作为测算节点，即可得到各园区第t年用电量，将这些数值组合后即可得到一个波动率测算集合{Qt0,Qt1,…,Qtm}，其中Qt0为典型园区用电量。由此，可得同类型园区用电量测算公式为：

(6)

(7)

5 算例分析

5.1 算例概况

本文以某增量配电园区为例，利用实物期权方法对该园区配电网投资进行分析。选取2017—2025年为测算周期。该园区于2017年开始规划建设，通过负荷预测可得园区未来各年容量需求及用电量预测结果如表2所示。

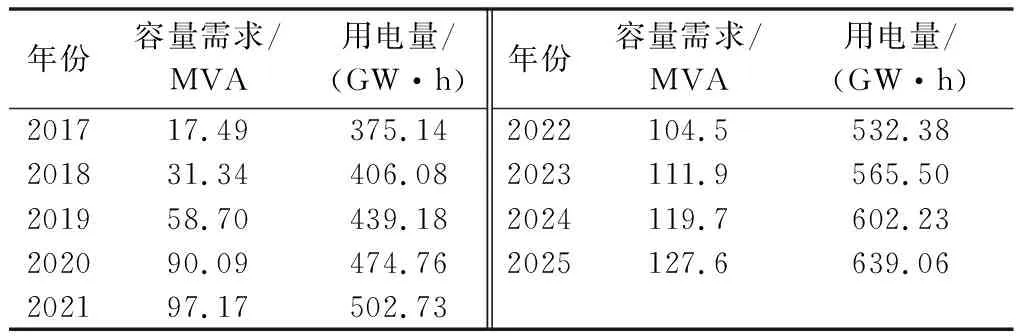
表2 某增量配电园区电力需求Table 2 Power demand for an incremental power distribution park

根据投资电压等级不同，可分为两种投资方案：方案1是投资110 kV电压等级配电网，在这一方案下配电网收益为110 kV与10 kV之间的价差，取0.03元/(kW·h)；方案2是投资220 kV电压等级配电网，在这一方案下配电网收益为220 kV与10 kV之间的价差，取0.04元/(kW·h)。为使得测算具有可行性，在此假设全部电量形成的价差的低电压等级均为10 kV，即假设园区内各用户均为10 kV用户，园区增量配电网单位电量投资收益为110 kV与10 kV之间的价差、220 kV与10 kV之间的价差。

依据容量预测结果，两种投资方案投资计划如表3所示。

表3 增量配电网投资计划Table 3 Investment plan of incremental distribution network

选取与该园区同类型的13个园区，采用本文构建的增量配电网投资收益波动率测算模型，得到典型园区配电网投资收益波动率，测算结果见附录A表A2。

取两年均值可得典型园区配电网收益波动率为24.5%。

5.2 投资决策分析

采用净现值方法，可测算得出两种方案下的净现值估值。在测算净现值时需进行如下假设：①由于测算周期未达到设备寿命周期，在测算净现值时假设在2025年设备除去5%残值外全部回收；②在园区配电网收益中只考虑园区最高电压等级与10 kV用户之间的输配电价价差，即假设所有用户均为10 kV用户。测算得方案1的净现值估值为-1 657.2万元，方案2的净现值估值为-2 283.0万元。根据传统投资决策原则，由于两种净现值估值均为负，说明投资方案不可行。从方案比选的角度，方案1优于方案2。

依据实物期权方法对两种投资方案进行分析，测算得出两种方案实物期权估值结果如表4所示。

表4 实物期权模型参数取值及其测算结果Table 4 Parameters of real option model and its measurement results

由测算结果可知，在考虑投资方案实物期权价值的情况下，两种投资方案的投资价值均为正，说明方案可行。同时，由于方案2期权价值更大，使得方案2总价值大于方案1，在这种情况下方案2更优。

选取波动率为敏感因素进行敏感性分析，以5%为波动值，分析结果如图1所示。

由敏感性分析结果可以看出，方案2对于波动率的敏感性要高于方案1，这主要是由于方案2投资收益较高引起的，同时也是在增量配电网投资中考虑220 kV电压等级变电站的一个重要原因。可以看出，随着波动率的增长，投资方案价值随之增大。采用插值法可知，当波动率减少至16.9%时，方案1总价值大于方案2，即低风险情形下，方案1优于方案2，这与净现值测算结果一致。

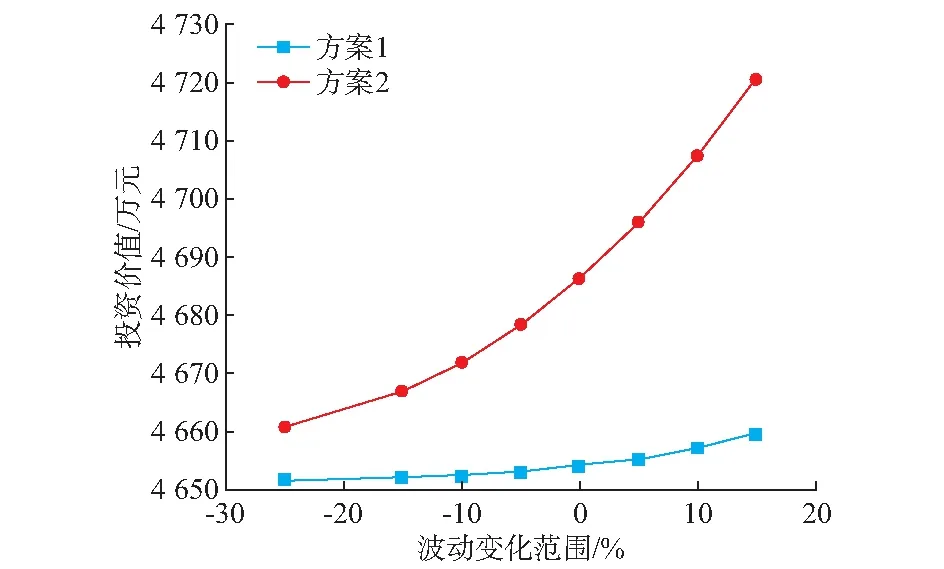
图1 波动率敏感性分析结果Fig.1 Analysis results of volatility sensitivity

6 结语

1)输配电价核算条件下，增量配电网投资收益取决于不同电压等级输配电价价差。增量配电网投资收益存在不确定性，包括负荷电量增长的波动性、不同投资方案带来的不确定性、投资刺激作用、多能互补及能源互联网等发展带来的不确定性，随着电网逐步发展，收益不确定性将逐步凸显。

2)本文构建了增量配电网投资价值估值模型，并针对模型参数提出确定方法，构建了基于横向对比分析的配电网收益波动率测算模型。该模型可以用于增量配电网投资决策，为决策者提供指导。

3)增量配电网投资收益不确定性较大，利用实物期权方法可以对增量配电网投资风险价值进行评估，有利于不确定环境下的电网投资决策，是对传统电网投资决策方法的补充。

本文研究了两阶段增量配电网投资的价值评估方法，但电网投资具有多阶段特性，各个投资阶段之间相互关联，并且存在博弈过程，针对多阶段增量配电网投资决策问题还有待于进一步研究。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。