适用于MMC型直流变压器的直流故障主动限流控制方法
丁 然, 梅 军, 管 州, 赵剑锋
(东南大学电气工程学院, 江苏省南京市 210096)
0 引言
高压大功率直流变压器作为不同电压等级之间线路互联以及新能源并网的关键设备[1],是构建柔性直流电网的重要技术保障。近年来,国内外学者将已经在高压直流(high voltage DC,HVDC)领域得到广泛应用的模块化多电平换流器(modular multilevel converter,MMC)技术[2-3]与高压大功率直流变换技术相结合,提出了MMC型直流变压器(MMC based DC transformer,MMC-DCT)拓扑,在未来HVDC电网中具有良好的应用前景[4]。
实际运行中,由于直流电网的低惯量和弱阻尼特性,因此HVDC电网耐受直流短路故障的能力较差,系统故障传播速度较快,对系统控制响应时间要求更短。虽然典型HVDC电网一般配置直流断路器,但其电力电子器件数量随直流电压和电流等级的升高呈现几何级增长趋势[5],系统成本大幅增加,因此依靠MMC-DCT自身结构和控制对直流故障电流进行限制已成为热点问题[6]。在文献[7]的基础上,文献[8]通过分析传统采用半桥子模块结构的MMC-DCT直流故障特性,得出可以通过MMC-DCT自身闭锁原副边两侧MMC实现直流故障隔离和故障电流自清除的结论。另外通过对桥臂电感支路的优化,也可使MMC-DCT在检测到直流故障后通过转移故障电流流经支路来隔离故障[9]。国内外学者通过对子模块或换流器拓扑进行优化[10-11],提出仅需故障侧MMC闭锁就能清除故障电流的一系列改进型MMC-DCT[4,12-14]。
以上研究需要对直流故障进行识别,因而换流器闭锁信号或故障电流支路转移信号一般滞后于故障发生后几毫秒才发出。由于在此期间故障电流迅速上升,增大了功率器件的电流应力,因此未必能满足直流电网快速限制故障电流的要求,有必要研究在故障发生瞬间依靠换流器自动动作、同时超前于故障识别的主动限流控制方法。文献[15]提出了一种适用于三端直流输电系统的控制策略,并采用比例—积分—微分(proportional-integral-differential,PID)控制器对桥臂电压进行动态调整,以实现在直流故障时非故障区域的穿越运行,但其控制环节较为复杂,且仅针对直流变压控制、而非常用的移相控制进行设计,因此直流变压器系统的快速动态响应能力和调压范围仍不够理想。文献[16]针对MMC型高压直流(MMC based HVDC,MMC-HVDC)系统提出了基于虚拟阻抗的过电流抑制策略,并基于通用的双闭环矢量控制策略,将实际电路元件的特性映射入控制系统,增大放电回路中的等效电抗,从而一定程度上抑制了直流故障引起的过电流,但其应用尚未扩展到MMC-DCT领域。
本文在对MMC-DCT的直流故障机理进行分析的基础上,对直流故障电流的上升过程进行了较详细的分析,并提出一种控制环节简单、参数调节容易的新型主动限流控制策略。
1 MMC-DCT的拓扑与基本控制方式
典型的MMC-DCT的拓扑如图1所示,交流侧为面对面(front-to-front,F2F)连接,采用变比为KT的中频变压器T进行隔离和电压匹配。MMC1为一次侧换流端,每个桥臂包含m个子模块(submodular,SM),每个子模块由2个绝缘栅双极型晶体管(insulated gate bipolar transistor,IGBT)器件S1和S2、2个反并联二极管D1和D2,以及1个直流侧电容CSM组成;MMC2为二次侧换流端,每个桥臂包含n个子模块;Lp和Ls分别为一、二次侧的桥臂电感;Udc1和Udc2分别为输入电压和输出电压。iLpx和iLnx(x=a,b)分别为MMC2各相的上、下桥臂电流;uac2为二次侧阀侧电压;Idc2为直流输出侧电流。所有子模块均采用图1中所示的半桥结构。
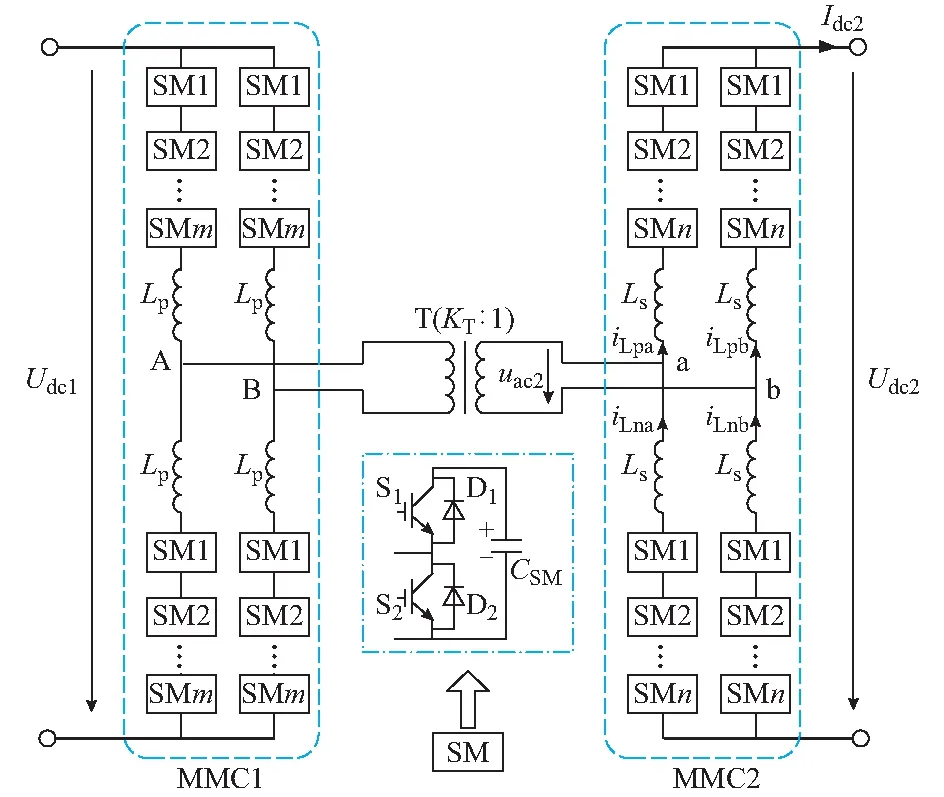
图1 典型的MMC-DCT结构Fig.1 Typical MMC-DCT structure
MMC-DCT的基本控制方式可分为直流变压控制和移相控制[17]。直流变压控制的调压范围受到中频变压器变比的限制;而移相控制(如附录A图A1所示),通过对MMC1和MMC2之间移相角的调节可以实现对功率的调节,具有系统动态响应快和变比不受限的优点,因而得到较多应用。
2 MMC-DCT直流故障分析
2.1 MMC-DCT直流故障的机理
在所有直流故障中,双极短路故障产生的后果最严重,因此本文以双极短路故障为例进行直流故障机理分析。如附录A图A2所示,当MMC-DCT中的MMC2直流侧发生双极短路故障时,桥臂电流iLpx和iLnx由MMC2结构中储能元件产生的放电电流iLx_SM与交流馈入电流iLpx_AC和iLnx_AC叠加而成,按不同时间段进行讨论,设t1为子模块电容放电完毕的时刻。
1)0≤t≤t1时间段
此时间段内放电电流iLx_SM由子模块电容放电产生。故障发生后,单相放电回路如附录A图A3所示,其等效电路为电阻—电感—电容(RLC)二阶电路,iLx_SM数值从0开始增大,假设在tpeak时刻iLx_SM达到峰值,此后逐渐减小。此时间段内交流馈入电流iLpx_AC和iLnx_AC由如附录A图A4所示的交流侧向MMC2馈入电流形成单相回路(以a相上桥臂与b相下桥臂为例)而产生。
在0≤t≤t1阶段放电电流iLx_SM在桥臂电流中占主导地位。桥臂电流iLpx和iLnx在0~tpeak时间段总体呈现振荡上升趋势;在tpeak~t1时间段总体呈现振荡下降趋势,但数值仍为正值[7]。
2)t>t1时间段
根据以上分析,桥臂电流在tpeak(0
2.2 MMC-DCT直流故障电流上升阶段分析
1)子模块放电电流的分析
附录A图A3所示单相电容放电回路的等效电路如图2(a)所示,是一个RLC串联二阶电路,S为开关,其中Lsum=2Ls;Csum=2CSM/n;Rsum为放电回路中所有等效电阻之和;uc和uc′分别为子模块电容电压及其交流馈入等值电路中子模块的等效电容电压;ILpa0和ILpb0分别为故障时刻a和b相上桥臂电流瞬时值;Idc0为故障发生时刻的放电初始电流;Udc0为放电初始时刻子模块电压之和[7]。
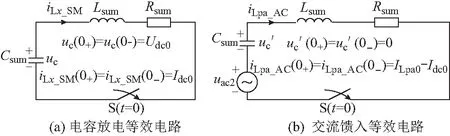
图2 直流故障后单相等效电路Fig.2 Single-phase equivalent circuit after DC fault
正常稳态运行时,MMC2的各桥臂电流由相同的直流分量与不同的交流分量叠加而成,其中直流分量由直流输出侧电流Idc2在两相间均匀分配得到[18],故有
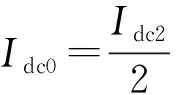
(1)
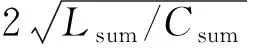
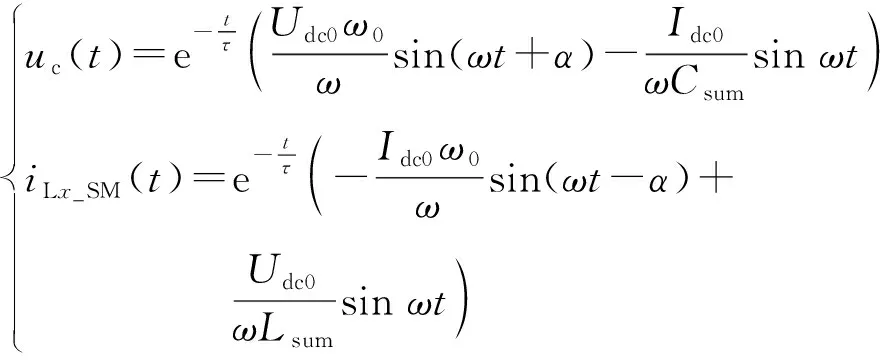
(2)
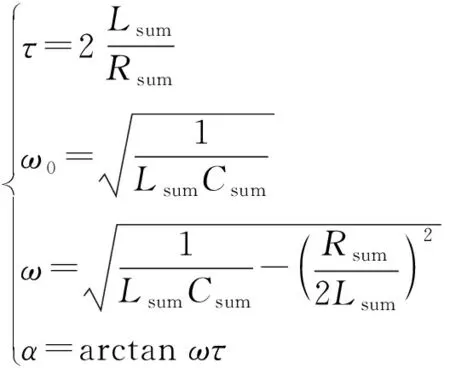
(3)
式中:τ为放电电流衰减时间常数;ω0为放电回路固有角频率;ω为放电电流的角频率;α为放电电流的初相角。
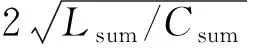
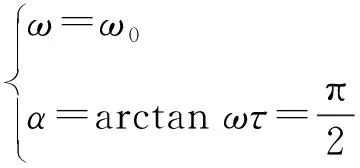
(4)
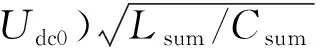
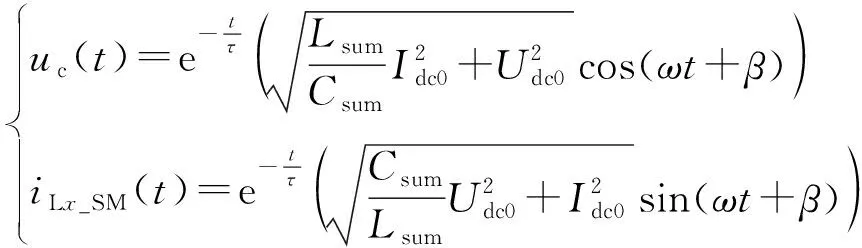
(5)
根据(π/2-β)∈(0,π),可知当k=0,ωt=π/2-β时iLx_SM取到第1个极值,此极值即为iLx_SM峰值,且此时uc为0,即iLx_SM到达峰值的时刻tpeak就是子模块电容放电完毕的时刻t1。因此有
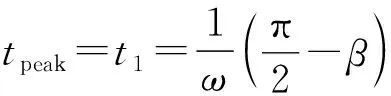
(6)
2) 交流馈入电流分析
文献[7-8,16]均忽略这一时间段的交流馈入。然而不同于工作在50 Hz工频下的MMC-HVDC,MMC-DCT一般工作在几百赫兹至1 kHz的中频段。由于直流系统保护一般在2~3 ms以内动作,交流馈入过程可能经历1个周期左右的时间,因此交流馈入电流iLpx_AC和iLnx_AC对桥臂电流的影响不应忽略。为了得到更准确的桥臂电流表达式,本文将交流馈入电路纳入考虑。设故障时刻a和b相上桥臂电流瞬时值分别为ILpa0和ILpb0。由附录A图A4可得a相上桥臂与b相下桥臂形成的单相交流馈入等效电路如图2(b)所示,电路初始电流(ILpa0-Idc0)为故障发生时刻桥臂电流中的交流分量瞬时值,uac2为交流馈入等值电路等值电压,假设
uac2=Uac2sin(ωTt+φ0)
(7)
式中:Uac2为uac2的峰值;ωT为变压器两端交流角频率;φ0为故障时刻uac2的初始相位。
图2(b)是一个正弦激励下的二阶欠阻尼电路,其全响应过程已在文献[19]中有类似分析,其电路的完全响应形式为:
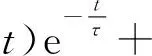
Ucmsin(ωTt+φc)
(8)
式中:Ucm为电容电压稳态响应分量峰值;φc为电容电压稳态响应分量初始相位;k1和k2为待定系数。
另有电容电流公式及电路初始条件:
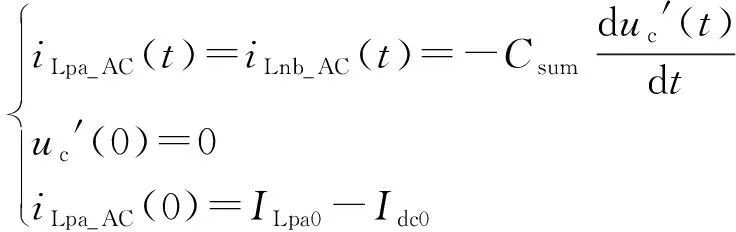
(9)
由式(8)和式(9)可确定k1和k2:
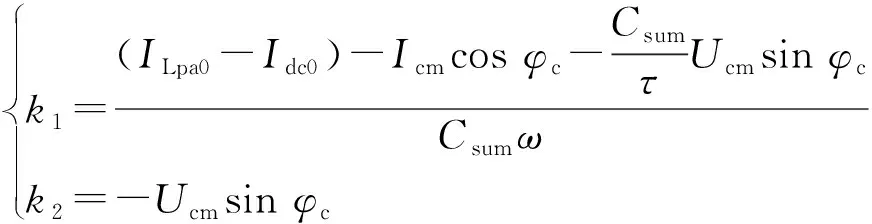
(10)
式中:Icm=ωTCsumUcm,为电容电流稳态响应分量。
将式(10)代入式(9)可得出交流馈入电流iLpa_AC和iLnb_AC表达式如式(11)所示,同理可得到iLpb_AC和iLna_AC表达式如式(12)所示,式中稳态分量可由相量分析法得到。
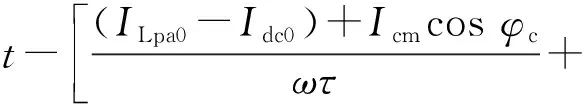
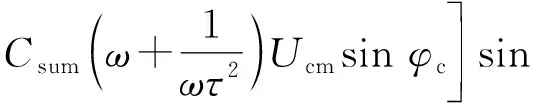
Icmcos(ωTt+φc)
(11)

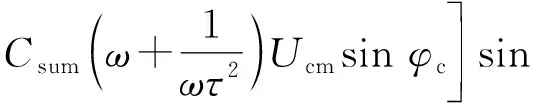
Icmcos(ωTt+φc)
(12)
(13)
由于桥臂电流由放电电流与交流馈入电流叠加而成,因此有
(14)
将式(5)、式(11)至(13)代入式(14)即可得出t1时刻前的桥臂电流iLpx和iLnx的准确表达式。
根据基尔霍夫电流定律,有
ILpa0+ILpb0=Idc2
(15)
由式(5)、式(11)至式(15),以及基尔霍夫电流定律可得出t1时刻前的故障点短路电流isc的表达式如下所示:
isc(t)=iLpa(t)+iLpb(t)=
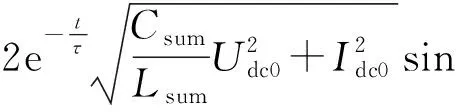
(16)
由式(16)可知isc与iLx_SM同时达到峰值,根据式(6) 可求得isc的峰值Isc_peak为:
(17)
式中:γ=(β-π/2)/ω。
由式(4)可近似认为(β-π/2)/ωτ=0,此时可化简式(17),得到故障点短路电流的峰值Isc_peak的表达式如下所示:
(18)
3 MMC-DCT的主动限流控制原理
由于桥臂电流实际影响IGBT等功率器件过电流程度,因此MMC-DCT的限流应以限制桥臂电流为目的。由于在桥臂电流上升阶段电容放电电流iLx_SM占主导地位[7],因此只要限制了电容放电电流iLx_SM,就可实现对桥臂电流的限制。尽管iLx_SM难以测量,但根据式(16)可知,通过测量isc就可以间接得出iLx_SM,因此为了实现MMC-DCT的直流故障主动限流控制,减少桥臂电流过电流的可能性,需要降低故障发生后isc的峰值Isc_peak,以及增大isc的峰值时间tpeak。
3.1 虚拟阻抗控制
根据式(18)可知,通过等效增大Lsum就可以实现Isc_peak的降低。虽然通过增大桥臂电感或在直流侧串联平波电抗器能够达到增大Lsum的目的,但可能影响系统的稳态特性,并增加系统成本。文献[16] 针对MMC-HVDC提出了基于虚拟阻抗的过电流抑制策略,通过设置包含直流侧附加虚拟阻抗的控制环节,可在发生直流故障时等效增大Lsum进行限流。该策略可推广应用在MMC-DCT中(如附录A图A5所示)。
3.2 新型主动限流控制
虽然在控制框图中加入虚拟阻抗环节能够等效增大Lsum,并在一定程度上降低故障点短路电流峰值Isc_peak,但是根据式(18),当各电路参数中仅有Lsum增大时,Isc_peak的减小幅度有限,而且故障点短路电流峰值时间tpeak未必增大,因此有必要研究效果更显著的限流方案。
一般情况下在故障发生后,MMC的调制方式与稳态运行时相同,以N+1调制为例,此时故障侧MMC上、下桥臂投入的子模块数量之和nsum=n。设USM0为系统稳态运行时子模块电压平均值,则放电初始时刻子模块电压之和Udc0=nsumUSM0,Csum=2CSM/nsum,代入式(18)得:
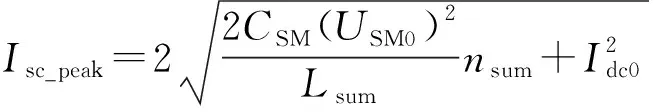
(19)
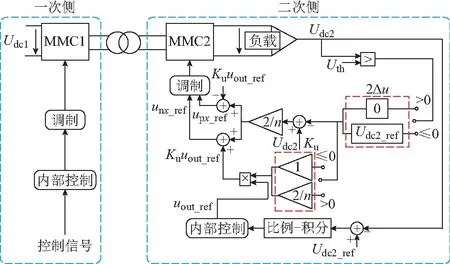
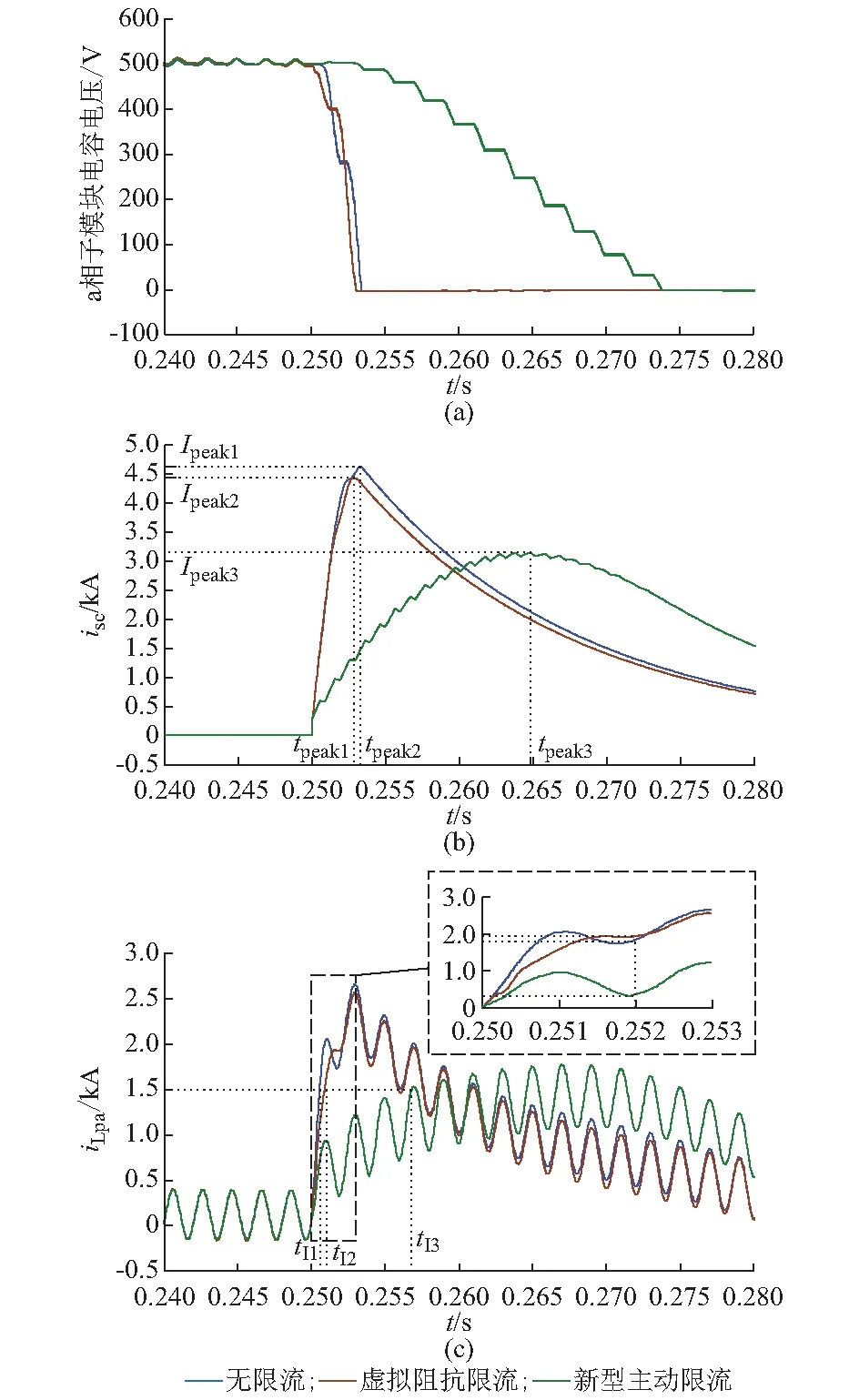
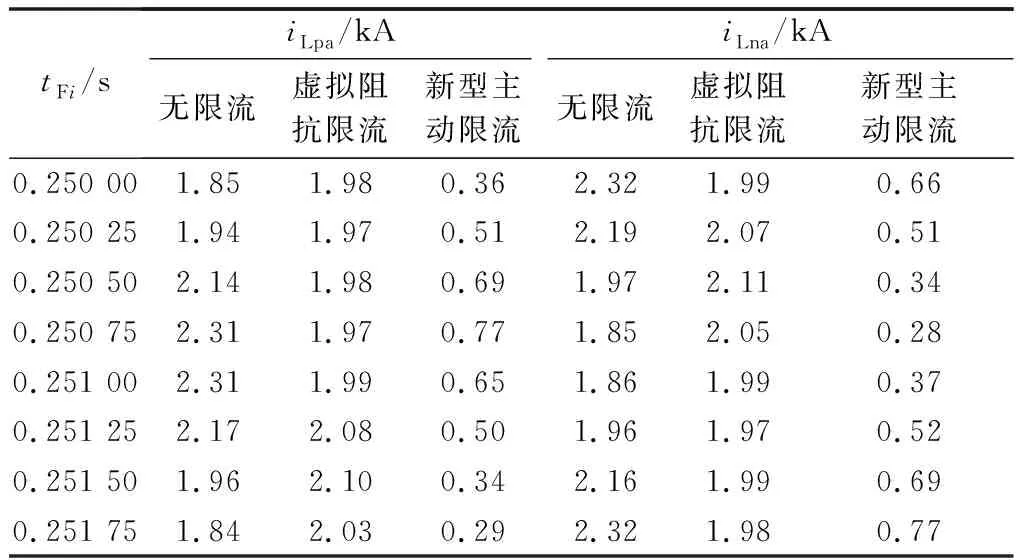
如果在故障发生后通过对调制方式的改变使nsum MMC2桥臂某一时刻上、下桥臂投入的子模块数量nx_up和nx_down,以及二者之和nsum由各桥臂电压upx和unx(x=a, b)决定,根据MMC的基本结构[18]有 (20) 式中:upx_ref和unx_ref分别为上桥臂电压参考值和下桥臂电压参考值;uout_ref为MMC2输出电压参考值。 upx_ref和unx_ref经调制环节分别得到上、下桥臂各自投入的子模块个数。以MMC领域常用的最近电平逼近调制(nearest level modulation,NLM)[20]为例,有 (21) 式中:round(·)为取整函数。 根据式(20)可知,桥臂电压参考值upx_ref和unx_ref由大小为Udc2/2的直流分量分别叠加交流分量uout_ref和-uout_ref组成,因此可通过分别调整直流分量和交流分量来实现upx_ref和unx_ref的调整。设置直流分量的附加偏置Δu以及交流分量的增益Ku,有 (22) (23) 式中:upx_ref′,unx_ref′,nx_up′,nx_down′,nsum′分别为上桥臂电压参考值、下桥臂电压参考值、上桥臂投入子模块数、下桥臂投入子模块、投入子模块总数的调整量。 当Δu=0,Ku=1时,upx_ref和unx_ref按照式(20)产生,nsum=n;当Δu>0,Ku=1时,upx_ref′∈[0,Udc2/2-Δu],unx_ref′∈[0,Udc2/2-Δu],随着Δu的增大,nsum逐渐开始减少,若Δu=Udc2/2,则桥臂电压参考值仅包含交流分量uout_ref和-uout_ref,且upx_ref′∈[0,Udc2/2],unx_ref′∈[0,Udc/2],nsum≤n/2;若Δu=Udc2/2,0 绘制Δu=Udc2/2,Ku=2/n,调制比为1时的桥臂电压参考值与桥臂子模块投入数量关系如附录A图A6所示。从图中可看出,调整前的桥臂电压参考值upx_ref和unx_ref按照式(21)使得nx_up∈{0,1,…,n},nx_down∈{0,1,…,n},nsum=n;由于附加偏置Δu和增益Ku的作用,调整后的桥臂电压upx_ref′和unx_ref′不含直流分量,且幅值降为Udc2/n,此时按照式(23)有nx_up′∈{0,1},nx_down′∈{0,1},nsum′∈{0,1}。 结合以上分析,设计如图3的主动式限流控制框图。设置输出电压阈值Uth,当系统稳态运行时,Udc2>Uth,Δu=0,Ku=1,上桥臂电压和下桥臂电压参考值upx_ref和unx_ref若仍按式(20)产生,则不会对系统稳态运行产生影响;当直流双极短路故障发生时,Udc2迅速下降使得Udc2≤Uth,从而使Δu从0跳变至Udc2_ref/2,Udc2_ref为Udc2的参考值,消除了桥臂电压中的直流偏置,同时Δu的变化使得Ku从1跳变至2/n,使桥臂电压中交流分量幅值下降;最后按式(22)得到调整后的桥臂电压参考值upx_ref′和unx_ref′传递给调制环节,从而使MMC2每相投入的子模块数从nsum=n减少到nsum′∈{0,1}。 图3 基于新型主动限流的MMC-DCT控制框图Fig.3 Block diagram of MMC-DCT based on proposed active current limiting control 采用如附录B表B1所示的参数在MATLAB/Simulink软件平台进行仿真实验。在故障时刻tfault=0.25 s时MMC2发生永久性双极短路故障。附录B图B1显示了新型主动限流控制下MMC2的a相上、下桥臂投入的子模块数量之和nsum在故障期间的变化,当故障发生后,nsum从nsum=4降低到nsum∈{0,1}。图4比较了直流变压器系统故障侧MMC2的故障点短路电流、子模块电压和桥臂电流在不同限流控制方法下的变化情况。 图4 不同限流控制方法下的仿真波形对比Fig.4 Comparison of simulation waveforms among different current limiting control methods 从图4可观察出,对比无限流控制时Ipeak1=4.63 kA的情况,虚拟阻抗限流控制将短路电流峰值降低到Ipeak2=4.44 kA,下降幅度并不明显;且由于子模块电容放电并未减慢,短路电流到达峰值的时间反而从tpeak1=0.253 3 s下降到tpeak2=0.252 9 s;而本文提出的新型主动限流控制方法由于使子模块放电的速度变慢,因此故障电流的峰值减少到Ipeak3=3.15 kA,下降幅度约32.0%,且由于子模块放电的速度变慢,短路电流的峰值时间上升到tpeak3=0.264 8 s,增加了约11.5 ms。 假设IGBT峰值电流为1.5 kA,观察图4中桥臂电流iLpa到达1.5 kA的时间分别为tI1=0.250 6 s,tI2=0.250 9 s,tI3=0.256 8 s,即虚拟阻抗限流控制和新型主动限流控制方法将桥臂电流到达峰值的时间分别延长了0.3 ms 和6.2 ms,说明在相同的峰值电流指标下,新型主动限流控制方法为保护动作争取的时间更为显著。 此外,分析图4中不同限流控制方法下桥臂电流iLpa波形在故障发生后3.5 ms内的总体趋势可知,虚拟阻抗限流控制可使桥臂电流在整体程度上降低,但降低幅度有限,在个别时刻如t0=0.252 s时桥臂电流瞬时值反而略高于无限流控制情况;而采用新型主动限流控制可使桥臂电流在这一阶段所有时刻都有所降低,且降低幅度大于虚拟阻抗限流控制。 故障后桥臂电流的变化与故障瞬间桥臂电流的交流分量瞬时值有关,由于故障发生的时间不确定,因此应比较不同故障时刻后桥臂电流的瞬时值。由式(14)可知对角桥臂电流值相等,因此只须记录a相桥臂电流瞬时值iLpa和iLna。考虑故障发生的随机性,在t=0.250~0.252 s一个交流周期内分别设置8个永久性双极短路故障发生时刻tFi(i=1,2,…,8),时间间隔为0.25 ms,记录iLpa和iLna在tFi时发生故障后2 ms时的瞬时值如表1所示。 表1 不同时刻发生故障2 ms后的桥臂电流瞬时值Table 1 Instantaneous arm current at 2 ms after different fault time 从表1可以看出,相比于不加限流控制的情况,虚拟阻抗限流控制在某些时刻可使桥臂电流瞬时值有一定程度降低,且降低幅度不大,其他时刻桥臂电流瞬时值有所升高;而加入新型主动限流控制后,所有时刻的桥臂电流瞬时值都有较大程度降低。如果在tFi时发生故障后2 ms时系统又发生闭锁动作,则此时IGBT电流应力较小,功率器件的安全裕度有所提高,系统可靠性也得到改善。 综合以上仿真结果可知,本文提出的新型主动限流控制方法能较好地抑制故障电流,证明了该方法的有效性和优越性。 本文阐述了MMC-DCT在双极短路故障下的直流故障机理,详细分析了直流故障电流的上升过程,并给出了桥臂电流瞬时值在上升阶段的表达式。通过探索短路电流的峰值和峰值时间的准确值,得出可以在故障瞬间通过改变桥臂电压降低上、下桥臂投入的子模块数量之和进行限流的结论。根据此结论,设计了一种新型主动限流控制方法并加以仿真验证。该方法具有以下优势。 1)相比虚拟阻抗控制,能较大程度降低短路电流峰值,提高短路电流峰值时间。 2)在相同的峰值电流指标下,可为子模块闭锁保护动作争取更多时间。 3)由于超前于故障识别,因此当故障识别完成发出系统闭锁信号时各功率器件面临的故障电流应力相比无限流措施时的故障电流应力有较大减小,从而可选用较小容量的功率器件,降低系统成本,进一步提高器件安全裕度和系统可靠性。 4)无须复杂的控制环节,且针对移相控制设计,控制简单,参数调节容易,可保证MMC-DCT具有快速的动态响应速度和较宽的调压范围。 新型主动限流控制方法仅考虑对子模块放电电流进行限制,未考虑对交流馈入电流进行限制,因此对直流故障后的交流馈入电流限制方法进行研究,实现更优的限流性能,是进一步的研究方向。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。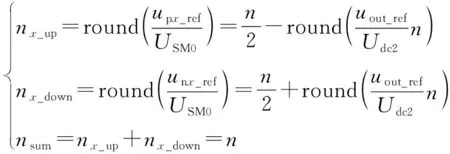
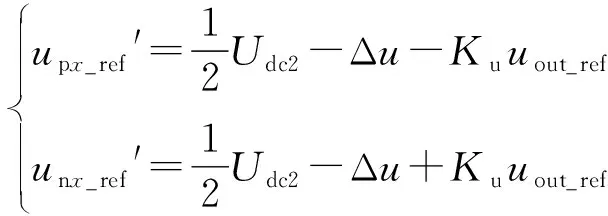
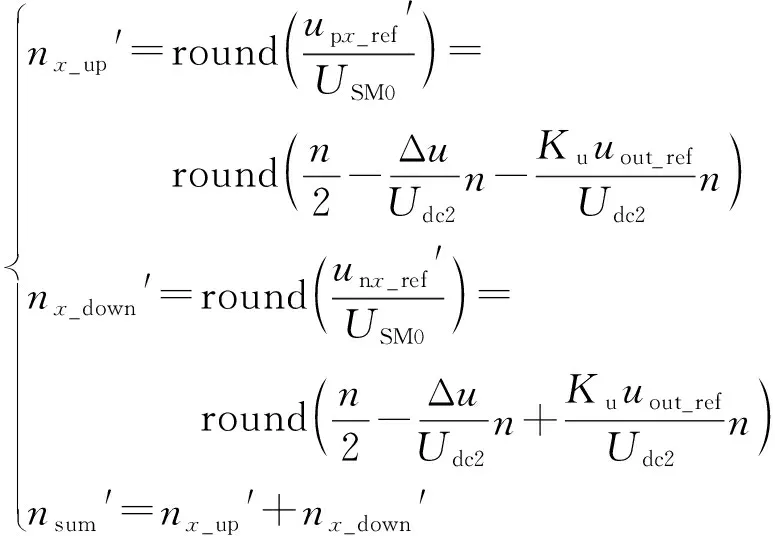
4 仿真验证
5 结语

