基于模块化多电平变换器的单相低频输电方法
欧朱建, 王广柱
(电网智能化调度与控制教育部重点实验室(山东大学), 山东省济南市 250061)
0 引言
中国学者王锡凡于1994年提出了三相低频(LFAC)输电方法[1],并相继对其基础原理、可行性、仿真及实验平台搭建等方面做了相关研究[2-4]。近年来,LFAC在国内外受到了广泛的关注,其中一个典型的应用为远距离海上风电并网[4-13]。由于输电频率下降,LFAC在输电容量和输电距离上均比传统高压交流(HVAC)输电更为优越[1-6]。由于LFAC仅有一个岸上换流站,其换流站的投资和维护均优于高压直流(HVDC)[6,10-11]系统。此外,LFAC还可解决HVDC输电中固有的问题,如直流电缆空间电荷积累问题[14]以及直流断路器的研制问题[15]。模块化多电平矩阵变换器(modular multilevel matrix converter,MMMC)通过级联结构,可将低耐压等级的功率器件用于中/高压大功率场合,且具备输入/输出谐波含量低、模块化设计、可靠性高、两侧功率因数可控等优点[12-13],将MMMC用于LFAC可进一步克服采用传统晶闸管相控变频器所带来的动态响应慢、谐波含量高、功率因数低、对无功控制不能独立于对有功功率的控制、需配置换流变压器等缺点[12-13]。然而,LFAC也存在以下不足:①低频频率范围受限[16];②需要三条输电线缆,且其输电密度小于HVDC。
文献[17-20]基于模块化多电平变换器提出一种交改直输电方案。该方案将传统三相交流输电改为三相直流输电,可大幅度提高系统的输电能力。其中,调制极采用分时段变极性输电,可视为一种低频输电方式[20],且该输电方式可解除对低频频率的限制。
本文进一步探索低频输电技术用于单相输电领域的可行性,并基于全桥模块的模块化多电平变换器(FMMC)提出一种单相低频(SLFAC)输电技术。与HVDC相似,SLFAC仅需两条输电线缆,且通过优化低频电压波形,其输电能力与HVDC相近。此外,SLFAC还可解决HVDC中的直流电缆空间电荷积累问题[14]、直流断路器的研制问题[15]、直流故障穿越问题[21]等。与LFAC相似,SLFAC的输电容量和输电距离要比传统HVAC要大,而且通过优化低频侧电压波形,可解除对低频侧输电频率的限制,实现1 Hz甚至更低频率的输电。目前尚未见到有关单相低频输电的文献报道。
与三相低频/直流输电不同,单相低频输电的低频侧存在功率波动(三相输电可通过三相对称抵消):一方面,低频侧功率波动不可流入工频电网,须全部由FMMC中的电容吸收;另一方面,须尽量降低低频侧功率波动,以提高SLFAC的输电容量及减小对FMMC电容电压的影响。针对上述问题,本文提出一种拟方波波形作为低频侧电压波形,可解除对低频频率的限制,且可减小低频侧功率波动;在此基础上,对HVDC,LFAC和SLFAC的技术经济性进行对比分析。提出了适用于FMMC-SLFAC的功率平衡策略,在保证系统有功平衡的前提下,实现低频侧功率波动全部由FMMC中电容吸收,不流入工频侧;在此基础上推导由低频侧功率波动引发的电容电压纹波表达式,给出了电容电压波动限幅范围内拟方波切换时长表达式。给出了适用于FMMC-SLFAC的综合控制策略,通过仿真验证其可行性和有效性。
1 FMMC-SLFAC的电路结构
图1为FMMC-SLFAC的电路结构图。与HVDC相似,FMMC-SLFAC由两个换流站组成:换流站1将电压由工频变换为低频;换流站2将电压由低频变换为工频。两个换流站通过电力线缆相连。换流站1的结构与换流站2相同。FMMC每相包含上、下两个桥臂;每个桥臂由N个SM子模块与电感L串联而成;每个子模块均为全桥结构;upx(upy)和unx(uny)(换流站1中x=a,b,c;换流站2中y=u,v,w)分别为上、下桥臂端口电压;ipx和inx分别为上、下桥臂电流;usx和isx分别为工频侧相电压和相电流。工频周期为Ts,频率为fs。uLF和iLF分别为低频侧相电压和相电流。低频周期为TLF,频率为fLF。本文仅对换流站1进行分析,将换流站2等效为阻抗ZL,如图1中虚线框内所示。
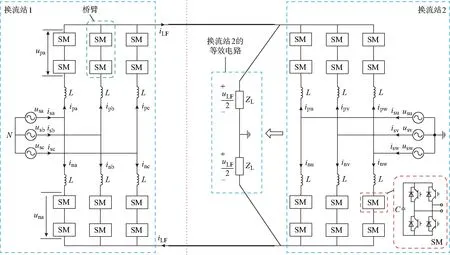
图1 FMMC-SLFAC电路结构图Fig.1 Structure of FMMC-SLFAC
2 低频侧电压波形
假设单相输电低频侧电压采用传统正弦波形,如图2(a)所示。

图2 低频侧电压波形设计Fig.2 Design of voltage waveform for low frequency side
假设
(1)
式中:UM和IM分别为低频侧相电压和相电流的幅值;ωLF为低频侧角频率;uLF和iLF分别为低频侧电压和电流;φ为初始相位角。
低频侧输送的瞬时功率pLF为:
pLF=2uLFiLF=UMIM(cosφ+cos(2ωLFt+φ))
(2)
由式(2)可见,低频侧包含二倍频功率波动,且波动幅值不小于传输的有功功率值,如图2(c)所示(图中,假设φ= 0,PLF=UMIM为有功功率)。一方面,较大的功率波动将会减小系统的输送容量;另一方面,功率波动不可流入交流电网,因而由低频侧功率波动引发的能量波动须全部由FMMC中电容吸收。由图2(c)可见,低频侧能量波动不仅与功率波动幅值有关,且与波动周期(即低频频率) 有关,周期越长,能量波动越大。较大的能量波动会导致电容电压产生较大的波动,影响控制精度。采用传统正弦波形不仅会在电容电压上引入较大的波动,且会限制低频侧输电频率。因此,传统正弦波形并不适用于SLFAC。
基于上述分析,本文提出一种拟方波波形作为低频电压波形,如图2(b)所示。该波形包含两部分:稳态部分,电压保持恒定;暂态部分(切换部分),电压波形为半周期正弦波。采用拟方波时,低频侧瞬时功率波形如图2(d)所示。由图2(d)可见,此时功率波动仅出现在切换部分。一方面,低频侧功率波动与低频频率无关,仅与切换过程时长有关,可实现1 Hz甚至更低频率的输电;另一方面,采用拟方波所引入低频侧的能量波动将远小于采用正弦波所引入的能量波动。此外,若稳态部分时长远大于暂态部分时长,则由切换过程造成的输送功率下降可近似忽略。此时,SLFAC与HVDC的输电能力近似等效。
有学者提出暂态波形可采用斜线波形[19],本文在此基础上将暂态波形进一步优化为半周期正弦波。该改进兼具两个优点:①由于半周期正弦波在切换起始和结束时刻的duLF/dt均为零,因而可减小由输电线路对地电容引起的充电电流;②可减小切换过程所带来的能量波动。附录A图A1阴影部分为采用两种切换波形所带来的能量波动。图A1(c)中采用斜线波形,图A1(d)中采用半周期正弦波,ULFm和ILFm分别为低频电压电流波形的正峰值,Tswi为切换过程正弦波的周期为40 ms。由图A1可见,采用半周期正弦波所带来的传输能量损失小于采用斜线波形的情形。
3 SLFAC与LFAC及HVDC的对比分析
3.1 SLFAC与LFAC的对比分析
在本节中,uy和iy分别表示LFAC低频侧的相电压和相电流;uxy和ixy分别表示LFAC中的桥臂电压和电流[15];下标M和max分别表示幅值和最大值。
1)LFAC和SLFAC拓扑中FMMC桥臂电压分别为[15]:
(3)
若LFAC和SLFAC两种拓扑低频侧相电压幅值相等,即Uy,M=ULF,M/2=UM,则由式(3)可知,两种拓扑桥臂模块数相同。当LFAC包含一个或者两个变流站时,SLFAC子模块数量分别为LFAC的4/3倍和2/3。此外,LFAC需要3条输电线缆,而SLFAC仅需2条。SLFAC在输电线缆投资及输电走廊面积方面具备优势。
2)设LFAC和SLFAC低频侧相电压和相电流幅值相等。根据式(2)可得LFAC最大传输有功功率为:
P3×3LF=1.5UMIM
(4)
式中:UM和IM分别为LFAC拓扑低频侧相电压和相电流幅值。
由第2节分析可知,理想情况下,SLFAC传输的有功功率可由HVDC传输的功率近似等效,因而SLFAC传输的有功功率可表示为:
PLF=2UMIM
(5)
式(4)和式(5)表明,当低频侧相电压和相电流幅值相等时,SLFAC传输的有功功率是LFAC的4/3倍。
3)设LFAC和SLFAC低频侧相电压幅值相等且桥臂电流限幅相同。忽略环流,可得LFAC和SLFAC桥臂电流分别为[15]:
(6)
假设工频侧和低频侧相电压幅值满足:
(7)
式中:M为常量。
根据功率守恒定律,LFAC和SLFAC拓扑低频侧相电流幅值与工频侧相电流幅值之比分别满足:
(8)
仅考虑桥臂电流最大值,据式(8)将式(6)重写为:
(9)
设定Ixy,max=ISLx,max,可得:
(10)
根据式(4)、式(5)和式(10)可得传输的有功功率满足:
(11)
取M值在0.5~1.5区间内,绘制PLF/P3×3LF和M的关系曲线如附录A图A2所示。由图A2可见,PLF/P3×3LF随着M的增大而增大。通常情况下M的取值范围为0.9~1,此时SLFAC传输有功功率约为LFAC的88%。
3.2 SLFAC与HVDC的对比分析
1)器件数量
当输出电压幅值相等时,SLFAC和HVDC包含子模块数量相同,即电容及桥臂电感数量相同,但SLFAC中开关管数量为HVDC的2倍。
2)传输容量对比
由于切换过程中,SLFAC输出功率下降,因而SLFAC传输容量略小于HVDC。当低频波形稳态过程时长远大于切换过程时长时,切换过程所造成的传输容量下降可近似忽略,两种输电方式的传输容量近似相等。
3)性能对比
由于SLFAC各子模块为全桥模块,因而相比于HVDC具备以下优势:①输出为低频交流,因而可克服电力电缆中的空间电荷积累问题;②存在输出电压为零点,因而无须直流断路器;③可解决HVDC中直流故障穿越问题。
4 功率平衡策略
4.1 功率平衡控制方法
为保证FMMC-SLFAC系统正常运行,需满足两个条件:①FMMC电容电压(系统有功功率)平衡;②低频侧功率波动全部由FMMC电容吸收,不流入工频侧。
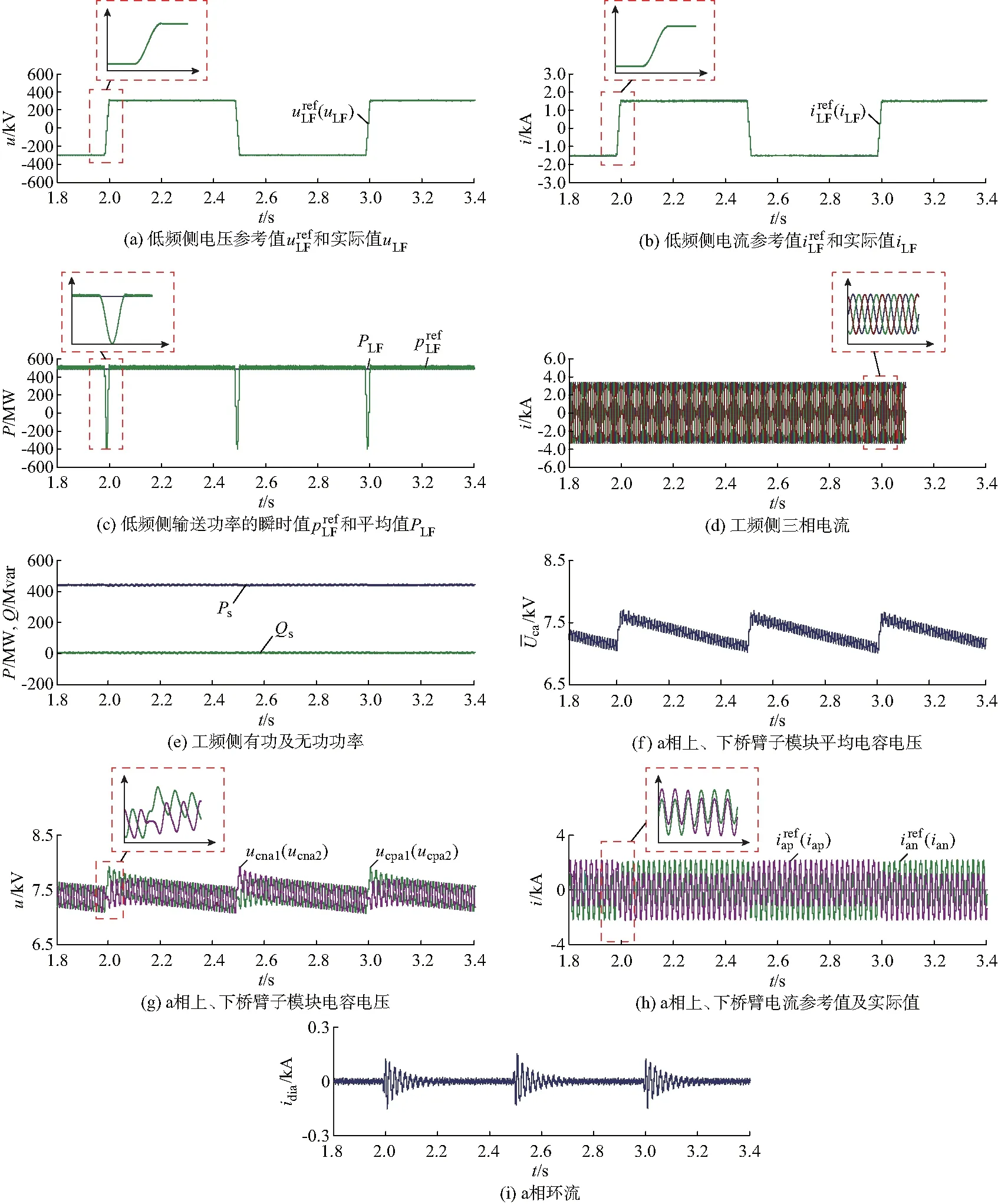
为满足条件①,工频侧瞬时功率ps和低频侧瞬时功率pLF需满足图3(b)所示的关系。低频电压切换过程中,低频侧瞬时功率将会由额定值降为零,再由零升为额定值。切换完成后,低频侧功率将保持恒定。对于工频侧而言,无论低频侧电压是否切换,工频侧功率保持恒定。图3(b)中,用pLF
为满足条件②,低频侧功率波动须全部由FMMC电容吸收,如图3(c)所示。pLF
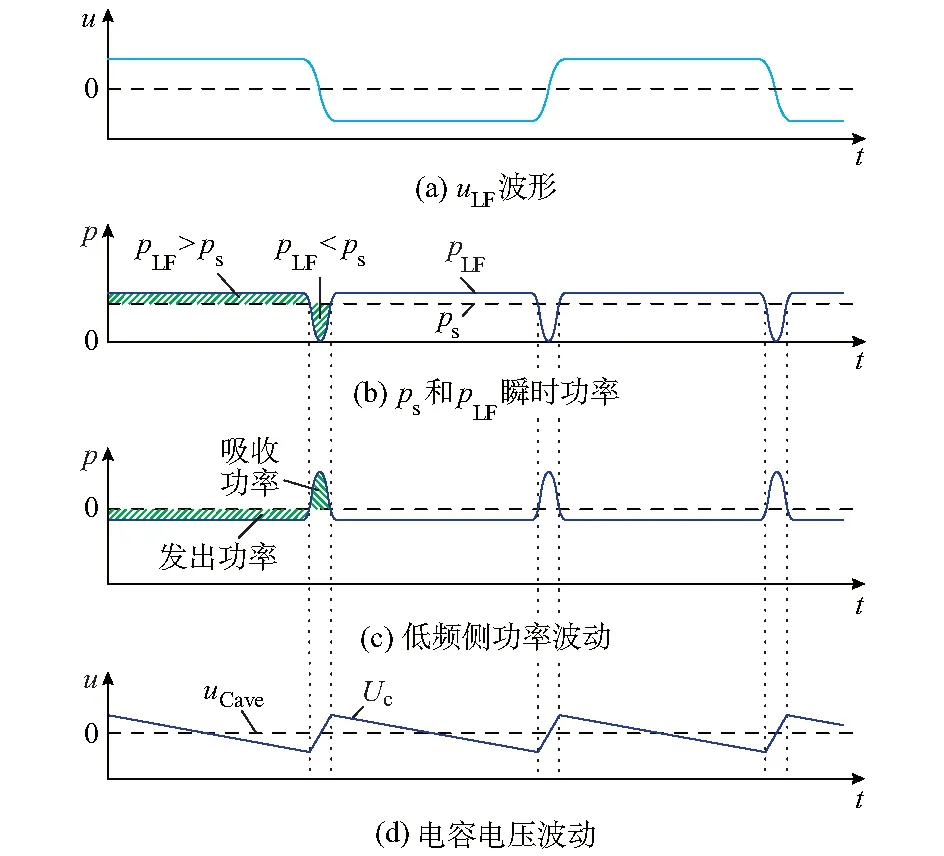
图3 FMMC-SLFAC的功率平衡策略Fig.3 Power balance strategy of FMMC-SLFAC
图3(d)是由低频侧功率波动引发电容电压波动的示意图。电容吸收功率时,电压Uc上升;电容释放功率时,电压Uc下降。随着低频侧切换的发生,电容电压将在额定值uCave附近产生微小的波动。
4.2 低频侧功率波动引发电容电压的波动
低频侧功率波动会引发电容电压波动,过大的电容电压波动会影响控制精度,甚至导致系统失控。因此,须对低频侧功率波动引发电容电压波动的大小进行计算,继而寻求合适的方式减小该部分电压波动。
切换过程中,低频侧输送的功率相比于额定值会下降。该功率差值可近似表示为:
ΔpLF≈ULF,MILF,M-uLFiLF
(12)
该功率差值在FMMC的6个桥臂间均分。稳态情况下,由该功率差值引入FMMC子模块直流侧电流可根据子模块交直流两侧的功率守恒得到,即
(13)
进而可得由该功率波动引发电容电压波动峰峰值为:
(14)
式中:ucLF为电容电压波动的峰值;C为电容。由式(14)可知,由低频侧功率波动引发的电容电压波动与ULF,M,ILF,M,Tswi,N,C,Uc有关。其中,Tswi与低频侧电压波形相关,为可控量,调整Tswi不会增加硬件成本。因而可通过改变Tswi来改变电容电压波动。
假设由功率波动引发的电容电压波动需满足:
(15) 式中:K为常量。 则由式(14)和式(15)可知,切换正弦波周期需满足: (16) 设K=5%,将表1中的参数代入式(16)可得: Tswi<60 ms (17) 本文取Tswi=40 ms。 稳态情况下,FMMC桥臂电压可表示为: (18) 桥臂电流可表示为: (19) 式中:ispx和isnx分别为上、下桥臂电流中工频电流成分;idix为x相环流,包含低频电流成分iLFx和高频环流成分icir,x。 由于本文采取桥臂电流控制,可自动抑制高频环流[22-23],因而进行功率分析时,可不考虑环流icir,x的影响。根据能量守恒定律可得功率关系为: Psx=Ppx+Pnx+PLFx (20) 式中:Psx为工频侧x相输入的有功功率;Ppx和Pnx分别为FMMC的x相上、下桥臂吸收的有功功率;PLFx为由FMMC的x相桥臂流入低频侧的有功功率。 各功率可表示为: (21) (22) (23) 式中:Ts和TLF分别为工频侧和FMMC的周期。 由式(21)可见,调整isx中的有功分量,可调整工频侧输入的有功功率Psx;由式(22)可见,调整桥臂电流中的低频分量iLFx,可调整低频侧传输的有功功率PLFx,进而可调整低频侧电压;由式(23)可见,上、下桥臂子模块有功功率各由两项组成,第1项分别与ispx和isnx相关,第2项与iLFx相关,即通过控制ispx和isnx或iLFx,均可控制上、下桥臂的有功功率,进而控制上、下桥臂的电容电压。当考虑上、下桥臂器件损耗存在差异时,可在上、下桥臂间引入与工频电压同频同相的微调交流有功电流分量Δisx,P,即 (24) 此时,流经上、下桥臂的工频电流为: (25) 实际中,桥臂内各子模块之间会存在差异,为此须微调子模块有功功率实现电容电压的平衡。 5.2.1低频侧电压控制 选取低频侧电流iLF控制低频侧电压uLF。假设三相桥臂均分低频侧电流,则 (26) 图4 FMMC-SLFAC控制策略Fig.4 Control strategy for FMMC-SLFAC 5.2.2层次化电容电压控制策略 桥臂电容电压控制采用如下层次化控制方法实现。 1)第1层为相桥臂级电容电压均值控制 2)第2层为上、下桥臂电容电压均衡控制 3)第3层为子模块电容电压微调控制 该层控制的目的为实现桥臂内各子模块电容电压的平衡。由于本文仿真环节桥臂子模块数较多,因而采用最近电平调制(nearest level modulation, NLM)实现子模块间的电容电压平衡,对此不作详细叙述。 5.2.3桥臂电流直接控制 本文电流环采用桥臂电流直接控制方法,其中桥臂电流控制器与文献[23]相同。由于桥臂电流同时包含工频电流、低频电流以及环流成分,通过控制桥臂电流可同时实现对3种电流成分的控制,无需独立的环流抑制器[23]。 考虑工频侧可能叠加无功电流,则根据式(19)可得FMMC上、下桥臂电流参考值为: (27) 根据式(27)可得FMMC-SLFAC控制策略如图4(d)所示。 本文通过在PSCAD/EMTDC中搭建系统级仿真来验证所提FMMC-SLFAC的有效性。仿真中所用参数如附录A表A1所示。仿真结果见图5。 图5(a)和(b)分别为低频侧电压和电流波形。由图可见,低频侧电压电流均呈拟方波形状,且实际值均很好地跟踪参考值,表明低频侧电压控制环节具有良好的稳态和暂态性能。 图5(c)为低频侧输送功率的瞬时值和周期平均值。由图可见,由于切换过程中瞬时功率下降,功率周期平均值略小于瞬时值峰值。在电压切换过程中,pLF 图5(d)为工频侧电流波形。由图可见,无论低频侧电压是否切换,工频侧三相电流幅值始终保持恒定。这表明低频侧的功率波动不影响工频侧。 图5(e)为工频侧有功及无功功率波形。由图可见,工频侧有功功率约为系统额定功率,且保持恒定,无功功率接近为零(无功功率可根据系统指令调整)。图5(e)表明低频侧功率波动不影响工频侧。 图5(f)为a相上、下桥臂电容电压平均值。切换发生过程中,电容吸收有功功率,电容电压上升;切换完成后,电容发出有功功率,电容电压下降。对比图5(f)和图3(d)可知,该波形与理论分析一致。而且由图5(f)可近似得到由低频侧功率波动引发的电容电压波动峰峰值约为0.25 kV,约为电容电压额定值的3.33%,该结论与4.2节所得结论一致。 图5(g)为a相上、下桥臂第1个和第2个的子模块电容电压值。从图中可以得出结论:①无论是否发生切换,各桥臂内子模块间的电容电压均保持平衡,表明子模块微调控制的有效性;②切换瞬间,上、下桥臂电容电压发生分叉(本文不对此现象做深入分析),但由于添加了上、下桥臂电容电压控制环节,上、下桥臂电容电压很快恢复平衡,表明上、下桥臂电容电压控制环节的有效性。 图5(h)为a相上、下桥臂电流参考值及实际值。由图可得结论:①桥臂电流完美跟踪其参考值,表明桥臂电流控制器具备良好的动静态性能,且表明电容电压波动对系统控制性能基本无影响;②低频侧电压每发生一次切换,低频侧电流同步反向,因而每当低频侧电压切换后,桥臂电流中的直流成分也会相应反向;③每次切换瞬间,上、下桥臂电流会产生较小的不对称。该不对称是由上、下桥臂电容电压控制环节所产生的工频环流造成,如图5(i)所示。该环流与工频电压同频同相,通过调整工频电流在上、下桥臂间的分配,实现上、下桥臂电容电压平衡。 本文基于全桥模块的FMMC提出了一种SLFAC输电方法。以一种拟方波波形作为低频侧电压波形,不仅可以解除对低频侧输电频率的限制,实现1Hz甚至更低频率的输电,而且可以减小低频侧功率波动以及电缆中的充电电流,使SLFAC的输电能力与HVDC相近。在此基础上,从技术经济性角度对LFAC,HVDC及SLFAC进行对比分析,表明所提方案的优越性和合理性。提出了功率平衡策略,不仅可以平衡FMMC的电容电压,也可使低频侧功率波动全部由电容吸收,不流入工频侧。在此基础上,推导得出低频侧功率波动对电容电压波动的影响,得到可通过改变低频侧电压切换时长来调整该影响的大小,并且在电容电压波动限幅范围内,给出了低频侧电压切换时长表达式。详细给出了基于桥臂电流直接控制的综合控制策略,通过仿真验证了所提FMMC-SLFAC的有效性和可行性以及良好的动静态性能。 图5 FMMC-SLFAC仿真波形Fig.5 Simulation results of FMMC-SLFAC 由图5(g)和图5(i)可见,低频侧电压切换瞬间,上、下桥臂电容电压发生分叉。为抑制该电容电压分叉,须叠加工频环流。进一步分析造成上、下桥臂电容电压分叉的原因并从根本上消除该电容电压分叉,从而避免引入工频环流是本文下一步的研究方向。此外,进一步对SLFAC,LFAC及HVDC从开关总容量、电容总容量等经济性指标方面进行详细对比分析,可进一步论证各方案的技术经济性,对不同的应用场合选取不同类型的输电方式具有重要的意义。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。
5 FMMC-SLFAC综合控制策略
5.1 功率分析和控制变量选取
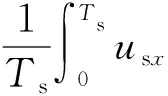
5.2 综合控制策略

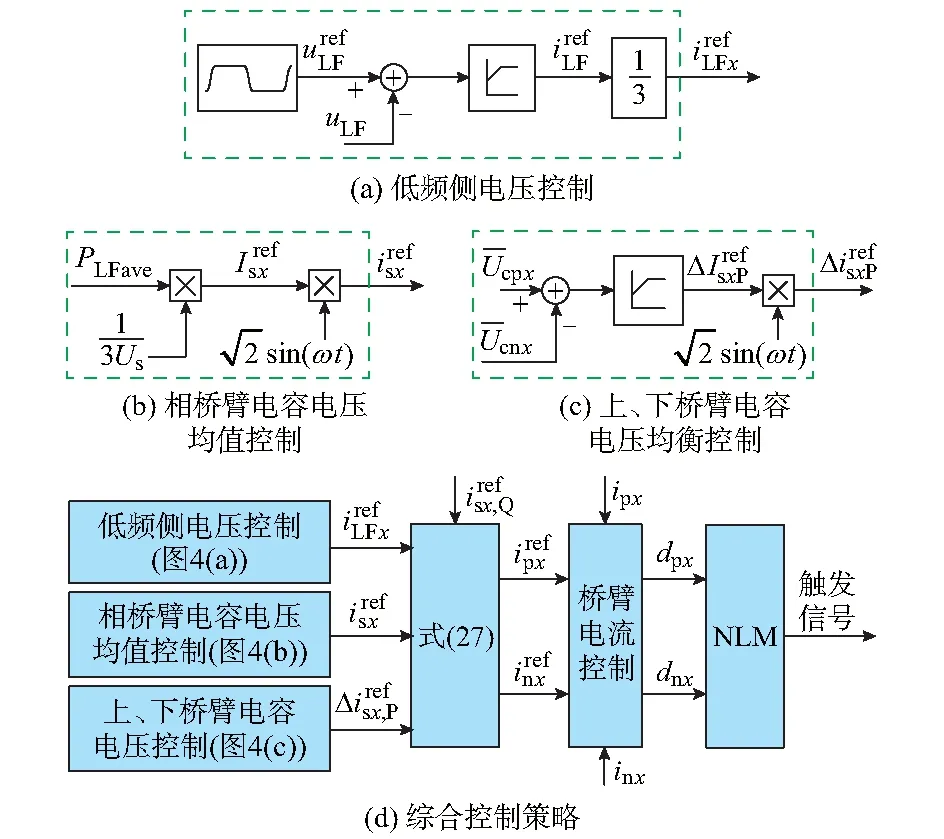
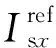


6 仿真验证
7 结语