适用于超大规模电网的在 线概率潮流算法

石 飞, 杨胜春, 冯树海, 王礼文

(中国电力科学研究院有限公司(南京), 江苏省南京市 210003)

0 引言

随着电力系统近年来的快速发展,源、荷双侧的不确定性因素越来越多。间歇性电源出力的随机性、电动汽车大量接入引起的集聚效应、负荷需求响应等各类因素的单独或综合作用都可能导致电网潮流特性及分布规律发生快速变化,传统确定性的在线安全分析和控制策略将难以满足系统安全稳定运行的要求[1-4]。而概率潮流计算方法可综合计及各类随机因素分析对电网影响,是解决此类问题的有效工具[4-6]。

概率潮流计算方法自1974年被提出后[7],历时40多年的发展已形成大量研究成果,形成了模拟法[8-10]、估计法[12-14]、解析法[15-18]等三类方法。以蒙特卡洛法为代表的模拟法将电力系统中的不确定因素作为随机变量建立概率模型,然后抽取概率分布的样本,最后统计输出变量的分布特征。该方法具有原理简单、适应性强的优点,但是为了满足精度要求,需要进行大量的仿真计算,用时长,一般作为其他方法的评价标准,很少应用于在线分析领域。点估计法属于逼近技术的一种,利用输入随机变量的统计信息来逼近输出随机变量的数字特征,其计算耗时与随机变量个数成正比,随机变量较多时,计算耗时较长。解析法中最常用的是半不变量法,根据输入量的分布函数,计算其半不变量,通过半不变量的代数运算代替复杂的卷积运算,提升了运算速度,且计算结果误差较小。目前,在现有各概率潮流算法中,半不变量法概率潮流计算速度最快,在线应用前景较好。该类算法目前已经在发电机组检修计划[19]、电力市场[20]、电网静态安全风险分析[21]和分布式发电的优化配置[22]等领域得到了广泛的研究与应用。

虽然半不变量概率潮流算法计算速度较其他概率潮流算法更快,但其计算速度受网络规模影响较大。当计算电网的节点数达到一定规模时,计算用时将明显上升。这主要是由于半不变量法计算过程中矩阵求逆及待求变量各阶矩的计算过程均为满矩阵运算,该部分计算用时与电网规模基本成平方关系,随着系统规模增大时,计算用时将明显增加。随着特高压持续建成投运,电网互联日益紧密,一体化特征愈加明显[23-24],而且,中国新能源资源与负荷中心的逆向分布特点,均要求从全局层面分析新能源出力波动性对系统带来的影响[25],从而对概率潮流算法的性能提出了很高的要求。为此,本文针对半不变量概率潮流算法的特点,对传统半不变量概率潮流算法进行优化改进,在保证计算精度的同时提升其计算速度,以适应超大规模电网在线分析的实时性需求。

1 半不变量法概率潮流

电力系统确定性潮流方程式可以简要概括为：

W=f(X)

(1)

式中：W为节点注入向量,包括节点注入有功功率及无功功率；X为节点状态向量,包括节点的电压幅值和相角。

将式(1)在基准状态X0处进行泰勒展开,并忽略高阶项,可得：

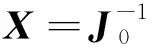
(2)

式中：J0为牛顿法潮流计算中的雅可比矩阵；S0为J0的逆矩阵,称为灵敏度矩阵；ΔW为扰动向量。

同理线性化支路潮流方程,当各节点状态变量已知时,支路潮流方程式可以写成如下形式：

Z=g(X)

(3)

式中：Z为支路潮流功率向量。

将支路潮流方程按照泰勒级数展开并忽略高阶项,可得：

ΔZ=G0S0ΔW=T0ΔW

(4)

式中：ΔZ为支路潮流功率向量的半不变量；G0为支路功率对节点电压求一阶偏导所得矩阵；T0为支路功率对节点注入灵敏度矩阵。

虽然式(2)和式(4)为线性变换,但当扰动向量ΔW为随机变量时,式(2)和式(4)的计算需进行随机量的卷积计算,计算量很大。通过引入半不变量与Gram-Charlier级数展开方法可以通过半不变量的简单代数运算获得随机变量的概率分布[3]。

半不变量的数学定义和描述涉及公式较多[27],本文不再详细描述。利用半不变量的相关特性,节点功率注入向量的k阶半不变量ΔWk及待求状态向量k阶半不变量ΔXk的求取方式如下：

(5)

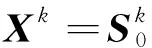
(6)

(7)

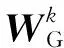
求得待求状态向量的各阶半不变量ΔXk后,通过半不变量与中心距的关系及Gram-Charlier级数展开方法,可求得ΔX的分布函数。

2 适用于超大规模电网的概率潮流算法

2.1 基于部分灵敏度矩阵的半不变量法

实际超大规模电网的计算模型中,随机变量多为新能源集中接入节点,此类节点相对全网总节点数而言比例很少,为此可对半不变量概率潮流算法进行适当改变,以提升计算速度。

按是否存在随机注入量,对参与计算的各节点进行分类,并将式(2)按该分类方式进行展开,可得如下形式：

(8)

式中：ΔX和ΔW的下标R表示含随机注入量节点,下标C表示常规节点；SRR为随机节点电压对随机节点注入灵敏度矩阵；SRC为随机节点电压对常规节点注入灵敏度矩阵；SCR为常规节点电压对随机节点注入灵敏度矩阵；SCC为常规节点电压对常规节点注入灵敏度矩阵。

根据半不变量概率算法的特点,各节点注入量的一阶半不变量可通过确定性潮流计算求取,无需通过灵敏度矩阵计算,而常规节点上节点注入的二阶以上半不变量均为零,即ΔWC中的元素全为零。因此灵敏度矩阵中的SRC和SCC无需计算,只需计算SRR和SRC。

由于确定性潮流计算过程中,已经形成了雅可比矩阵J0的因子表[28],因此计算SRR和SRC时,可直接利用因子表,按原先确定性潮流计算的消去顺序逐列快速求取。

(9)

式中：SR=[SRRSCR]T；E为单位矩阵。

求解SR第i列的列向量SRi时,可表示为：

ei=J0SRi

(10)

式中：ei为单位列向量,除第i行为1外,其他行均为0。

式(10)与确定性潮流计算迭代方程形式完全相同,J0中的元素也与确定性潮流计算最后一次迭代时一致,因此,可利用其因子表快速计算求解SRi,避免矩阵求逆。

计算SR后,可按照传统半不变量概率潮流算法进行求解,对应的电压灵敏度矩阵方程变为：

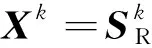
(11)

同理,支路功率的求取方法如下：

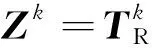
(12)

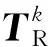
2.2 基于网络分解与等值的半不变量法

当系统中存在较多的随机变量时,采用求部分灵敏度矩阵的方式,效果不明显。为此,本文提出了一种基于网络分解与等值的半不变量概率潮流算法,通过将互联大电网拆分成若干个子网络独立计算,以提升计算速度。

首先介绍网络分解与等值算法对多区域互联电网的计算处理方法。如图1所示,将互联大电网按照边界节点进行撕裂,分成几个相互独立的子网络,仅通过撕裂节点与其他子网络相连[29]。

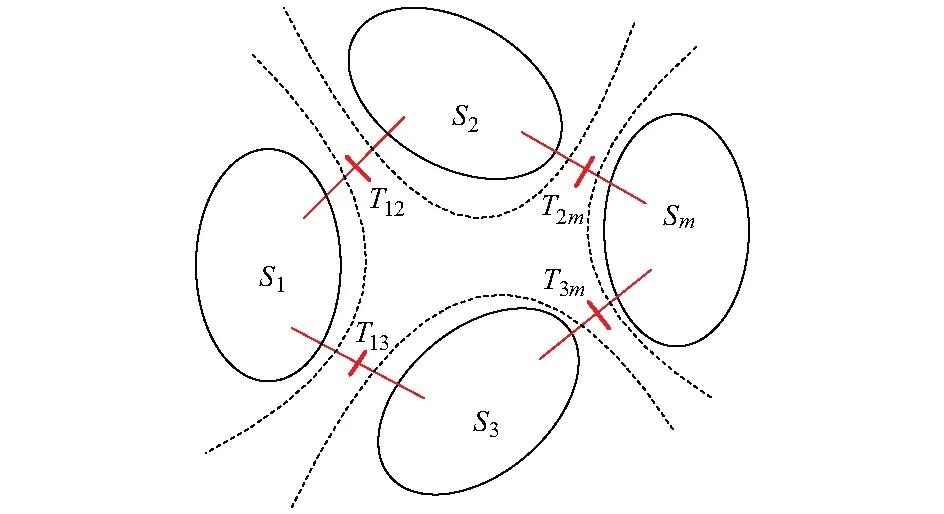
图1 互联电网分解示意图Fig.1 Schematic diagram of interconnected power grid decomposition

对第k个子网络计算时,可消去其他子网络,仅保留撕裂节点,详细等值消去方法见附录B。等值后,式(2)可表示成如下形式：

(13)

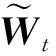
图2为式(13)的等值效果。以图1中的子网络S1为例。计算时,计算模型中只包含其内部节点与撕裂节点,与其他子网络无关。由此可将互联大电网拆分成若干个子网络进行独立计算。

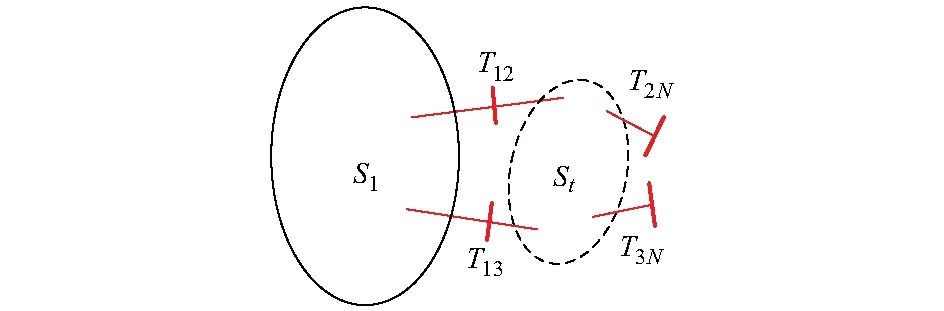
图2 子系统等值模型示意图Fig.2 Equivalent model of sub-system

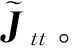
式(13)虽能用于确定性潮流计算,但无法直接用于半不变量法概论潮流计算,主要原因在于外部注入量的等值过程中,大量外部随机注入量被等值到撕裂节点上,撕裂节点上等值注入量不仅大小与原先存在较大差异,且撕裂节点间的相关性与等值前存在很大的差异,直接计算将存在很大误差。由于外部随机变量削减的过程为线性变化,因此,可根据随机变量线性变化的一些性质,计算等值后撕裂节点间的相关性系数。详细计算过程见附录B。

计算出等值后任意节点上的相关性系数后,可按照新的相关性系数矩阵对各子网络进行独立半不变量法概率潮流计算[18],相关计算公式较多,此处不再详细介绍。

3 算例分析

首先分析电网规模对半不变量概率潮流算法计算用时的影响。

采用传统半不变量概率潮流算法分别对IEEE 118节点系统、省级电网(1 079节点)、matpower5.0包case3120sp系统(3 120节点)、区域电网(8 632节点)进行概率潮流计算。每个系统均设置有50个随机变量,相同软硬件运行环境下,算法耗时与系统规模关系如表1所示。

表1 传统半不变量法计算耗时Table 1 Computational time of conventional cumulant method

如表1所示,当计算系统的节点数增加后,半不变量概率潮流算法的用时将明显上升,对8 632节点系统进行计算时,用时接近5 min,已无法满足在线分析的要求。采用本文所提出的基于部分灵敏度矩阵的半不变量法(下文简称方法1)对各系统重新进行计算,统计计算用时,并与原传统半不变量法进行对比,对比结果如表2所示。

表2 方法1计算耗时Table 2 Computational time of method 1

表2中,采用本文所提出的基于部分灵敏度矩阵计算方法对大电网进行概率潮流分析时,计算用时明显降低,满足在线分析需求。

与传统半不变量法相比,基于部分灵敏度矩阵算法的计算过程未做任何简化与假设,仅是对大量无关计算的削减,并充分利用了雅克比矩阵的稀疏性,因此其计算准确性与传统半不变量法完全相同。为验证基于部分灵敏度矩阵计算方法的准确性,采用IEEE 118节点系统进行计算分析,假定发电节点中85,110,113和116为风机接入点,其他发电机为常规机组。风机有功出力服从正态分布N(100,30),常规机组出力保持恒定。另外,假设系统中有功功率超过20 MW的负荷其功率大小同样存在波动性,服从正态分布N(Pload,10%Pload),其中,Pload为负荷基态有功值。利用本文提出方法1进行计算分析,并以20 000次蒙特卡洛计算结果作为判断标准,对本文方法的准确性进行验证。附录A表A1为方法1计算误差分布,由表A1中计算结果可以看出,本文所提方法与蒙特卡洛法的计算结果基本一致,表明本方法具备较高的计算精度。

为验证基于网络分解与等值的半不变量算法(下文简称方法2)的准确性,同样采用IEEE 118节点系统进行计算分析,假定发电节点中85,110,113和116为风机接入点,其他发电机为常规机组。风机有功出力服从独立正态分布N(100,30),所有负荷服从独立正态分布N(Pload,10%Pload),常规机组出力保持恒定。以节点23,47,49和65为分裂节点,将IEEE 118拆分成两个子网络,拆分方式详见附录A图A1。采用本文所提出的基于网络分解与等值的半不变量法进行分析计算,并与全网统一计算进行对比,统计结果见附录A表A2和表A3。

本文所提的基于网络分解与等值的半不变量法与全网统计计算效果基本一致。需要注意的是网络分解与等值过程中,分裂节点间的相关性系数对计算结果存在较大影响,如不考虑分裂节点间的相关性的改变,仅采用确定性潮流分析的等值方法,则会造成较大计算误差。以S2系统计算过程为例,等值计算过程中,边界节点间有功波动的相关性系数计算结果见附录A表A4。由表A4中结果可以看出,等值后的分裂节点上功率注入量存在明显的相关性,相关性的大小与外部随机变量的分布及网络结构均有关系。若不重新计算分裂节点间的相关系数,简单认为撕裂节点上注入量相互独立,将会存在较大误差。

附录A表A5为不考虑撕裂节点上相关性时的误差统计结果。由表A5可以看出,若不考虑分裂节点间相关性系数的变化,将会对计算结果造成较大误差。本算例中该计算条件下,误差较大的支路为：65-68,47-69,49-69和68-69,均为边界支路及平衡节点附近支路,同样表明计算误差的原因在于外网随机变量到分裂节点的等值过程。

为验证基于网络分解与等值的半不变量算法的计算速度。将8 632节点系统分别拆分成2,4和8个子系统独立计算,计算用时统计如表3所示。

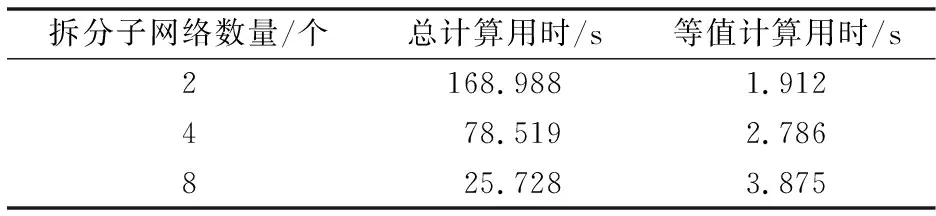
表3 方法2计算耗时Table 3 Computational time of method 2

由表3可见,当随机变量较多时,通过将互联大电网拆分成若干个子网络,虽然增加了部分等值计算用时,但此部分计算耗时较少,总体而言,该方法能有效提升大电网系统的计算速度。

此外,本文所提两种方法分别适用于超大规模电网在线概率潮流计算的不同场景。附录A表A6记录了不同随机变量情形下,方法1的求解用时变化情况,方法2计算用时与随机变量个数无关,计算用时同表3。如附录A表A6所示,方法1计算用时随着随机变量个数的增加而明显增加。8 632节点系统的仿真计算过程中,当随机变量数达到1 500左右时,方法1计算用时将超过方法2。因此实际应用过程中,应根据求解模型中随机变量的个数,选择合理计算方法。

4 结语

针对半不变量概率算法计算方法受网络规模影响较大这一问题,本文对传统半不变量概率潮流算法进行了改进与提升。当随机变量较少时,通过求取部分灵敏度矩阵的方法减少计算量；当随机变量较多时,采用网络等值与分解的方法减小待计算电网规模。本文所提改进方法在保证计算精度的同时,有效提升了半不变量概率潮流算法的计算速度。通过对IEEE标准算例计算结果的分析对比,验证了本文所提方法计算结果的准确性；通过对若干规模较大电网模型的分析计算,证明了本文所提方法能有效提升半不变量概率潮流算法的计算速度,可更好地适用于计及不确定因素的大电网一体化分析决策。

本文所提方法涉及两种不同算法,网络规模和随机变量数量是算法选择依据。但目前在选择标准方面尚无有效量化手段,实际工程应用中,部分场景下仍需根据通过计算对比,选择适用的算法。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。