基于分层控制的光—储—燃直流供电系统能量管理方法
薛 花, 胡英俊, 董丙伟, 王育飞
(上海电力学院电气工程学院, 上海市 200090)
0 引言
近年来,光伏发电成为最有发展前景的可再生能源发电技术之一。同时,燃料电池由于其绿色、高效,灵活的模块化结构和稳定的功率输出,也正成为广泛应用的绿色能源之一[1-3]。然而,光伏发电具有间歇性、随机性的不足,燃料电池由于内部电化学和热力学反应缓慢的原因难以快速响应光伏发电和电力负荷瞬变[4-5]。为了进一步提升供电质量,结合超级电容和蓄电池,共同构成的光—储—燃直流供电系统能够平滑光伏输出功率波动,同时提升供电可靠性,因而得到了越来越多的关注与应用[6-7]。
针对光伏/燃料电池/蓄电池/超级电容组成的光—储—燃直流供电系统,实现各电源间的协调控制与能量最优分配是混合直流供电系统进一步推广应用的关键所在。现有能量管理方法中,模糊控制[8]、小波变换[9]、反馈线性化[10]等给出了有效可行的控制策略。然而,上述方法应用于一种或两种混合电源供电系统是可行的,但因计算复杂,现有方法应用于具有多电源特点的光—储—燃直流供电系统时,难以同时实现快速动态响应、高稳定性和鲁棒性。模型预测控制(MPC)方法利用系统模型预测未来的控制输入和对象响应,可根据给定性能要求滚动求解最优控制律,具有灵活的多输入多输出处理能力,结构简单且动态响应性能优良[11-12]。文献[13]针对超级电容/蓄电池组成的混合电源,提出MPC方法,求取系统约束条件下超级电容和蓄电池的最优脉宽调制(PWM)占空比,实现系统稳定、协调控制,验证了模型预测方法在储能系统能量管理中的有效性和可行性。文献[14]针对燃料电池/蓄电池/超级电容轨道电车系统,采用线性比例—积分(PI)控制方法,实现超级电容参考电流的有效跟踪和直流母线电压的稳定;采用MPC方法,求取燃料电池与蓄电池的参考电流,实现系统能量管理,但须分别对超级电容、燃料电池和蓄电池进行独立控制,使得控制器结构复杂,计算量大。文献[15]建立了燃料电池/蓄电池/超级电容的统一动态简化控制模型,在给定工作点设计模型预测控制器,结合PI控制实现了直流母线电压平稳和系统协调控制,但外部干扰大幅变化或模型内部参数发生摄动的情形未做考虑。同时,传统的PI控制器通常基于特定工作点设线性控制,当光伏出力大幅快速波动或系统参数发生摄动时,会出现难以保证控制系统性能的问题[16-17]。
与传统PI控制方法不同,滑模变结构控制[18]、无源性控制[19]等非线性控制方法从能量稳定角度出发,针对变流器控制存在外部干扰和内部参数摄动的应用场合,设计全系统渐进稳定的控制律,同时能够确保动态响应特性。然而这些方法设计较为复杂,参数优化困难,限制了这些非线性控制方法在实际工程中的应用推广。非线性微分平滑控制方法其相较于上述非线性控制方法,通过期望的平滑输出轨迹对系统的状态量和控制量进行完整描述,避免近似处理,直接补偿非线性分量,结构简单,并能对系统高频未建模部分以及内外扰动进行抑制,稳定域宽,鲁棒性强,近年来在变流器稳定控制方面取得了长足进展。文献[20]设计微分平滑控制器实现直流永磁电机期望角速度轨迹的快速跟踪和DC-DC Buck变流器参数摄动情形下的鲁棒控制。文献[21]针对光伏、燃料电池、储能蓄电池混合系统的DC-DC变流器,提出微分平滑控制方法,并与传统PI控制方法做了比较分析,仿真结果验证了微分平滑控制方法能够在保持系统动态响应性能的条件下进一步提高稳定性,综合性能优于PI控制。然而,现有的非线性平滑可微方法在实现燃料电池和储能单元稳定控制的同时,难以完成考虑储能单元充放电速率限制下的多电源间功率优化分配任务。因此,亟须提出一种简单、高效的控制架构与方法,能够实现光—储—燃直流供电系统多电源稳定运行的同时,考虑蓄电池、燃料电池实际运行中需要限制电流充放电速率的需求,实现多电源间的能量最优分配与管理。
为实现光—储—燃直流供电系统的稳定运行和最优协调控制,提出一种基于光伏/蓄电池/超级电容/燃料电池的分层能量管理方法。上层控制设计微分平滑方法,获得下层控制所需非近似处理的总载荷电流期望轨迹,确保存在负载突变或光伏剧烈变化的情况下,系统依然能够快速跟踪期望轨迹,使系统直流母线电压稳定运行;下层控制设计模型预测方法,通过加权调节系统储能单元与燃料电池的充放电速率,实现混合直流供电系统多电源间功率的合理分配。基于MATLAB/Simulink的仿真结果表明:所提出的分层控制策略可以快速稳定系统直流母线电压,实现燃料电池/蓄电池/超级电容的协调控制,具有结构简单、响应速度快、稳态偏差小、鲁棒性强的特点。
1 光—储—燃直流供电系统分层控制策略设计
1.1 系统拓扑描述
由光伏电池/燃料电池/蓄电池/超级电容构成的光—储—燃直流供电系统如附录A图A1所示。光伏电池及燃料电池通过升压变换器接入直流母线;蓄电池以及超级电容通过双向DC-DC变换器接入直流母线;光伏电池、燃料电池、蓄电池、超级电容变流器并联运行。因多相交错并联变流器具有电路简单、输出功率范围宽、输出电压、电流纹波小的特点,将其应用于光—储—燃直流供电系统[22-23]。
光—储—燃直流供电系统中,为了最大可能利用太阳能,光伏电池采用最大功率点跟踪(MPPT)控制。燃料电池具有稳定功率输出的特点,在光伏发电不能满足负荷功率需求的情况下,由燃料电池补足功率缺口,使系统满足供需平衡。利用蓄电池能量密度高而功率密度小和超级电容功率密度大而能量密度小的特点,由蓄电池和超级电容组成优势互补的混合储能系统[24-25],主要用于平稳光伏电池出力波动,其中蓄电池承担波动功率中的低频部分,通过充放电稳定直流母线电压;超级电容承担波动功率中的高频部分,通过快速充放电响应,抑制功率突变对蓄电池和燃料电池造成的冲击。
1.2 上层控制方法设计
由非线性平滑微分理论可知,若非线性系统满足状态变量x和输入变量u可由输出变量y及其有限阶导数表示:
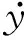
(1)
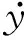
(2)
式中:φ(·)和ψ(·)表示映射方程。
同时输出变量可由状态变量、输入变量及其有限阶导数表示:
y=φ(x,u,u,…,u(α))
(3)
则该非线性系统为平滑系统。
由式(1)、式(2)的逆向动态方程可以看出,通过映射方程φ和ψ可以得到一个直接反映整个系统行为的量,使得系统的轨迹(x,u)由y及其导数直接获得,且不包含轨迹(x,u)的微分项和积分项,则通过Lie-Bäcklund同构方法,被控对象可通过反馈等价为任意的线性可控系统[26-27]。
为了实现上层控制非线性微分平滑策略在系统直流母线电压调节中的作用,确保存在负载突变或光伏剧烈变化的情况下,系统依然能够快速跟踪期望轨迹,使系统直流母线电压稳定运行。定义光储直流供电系统中各电源的功率和负载功率为:
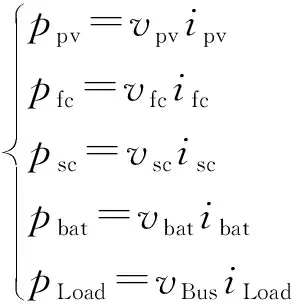
(4)
式中:ppv,pfc,pbat,psc分别为光伏电池、燃料电池、蓄电池和超级电容输出功率;pload为系统直流负载功率;vpv和ipv分别为光伏电池电压和电流;vfc和ifc分别为燃料电池电压和电流;vsc和isc分别为超级电容电压和电流;vbat和ibat分别为蓄电池电压和电流;vBus和iLoad分别为系统直流母线电压和系统直流负载电流。
系统直流母线电容存储能量EBus表示为:
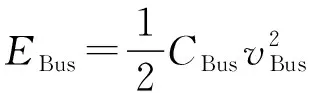
(5)
式中:CBus为系统直流母线输出电容;vBus为系统直流母线电压。
直流母线电容能量EBus的导数可表示为:
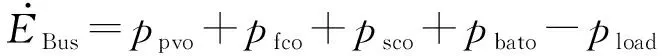
(6)
式中:ppvo,pfco,psco,pbato分别为光伏电池、燃料电池、超级电容和蓄电池输出至直流母线的功率。其中光伏电池输出功率ppvo采用MPPT控制,实现光伏发电功率最大功率输出[28]。
定义式(6)中pfco+psco+pbato=pHPSo,则直流母线电容能量EBus的导数可表示为:
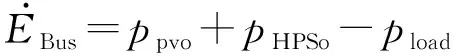
(7)
式中:pHPSo为系统总载荷参考功率。
燃料电池变流器、蓄电池变流器和超级电容变流器的并联静态损耗用rHPS表示,则pHPSo可表示为:
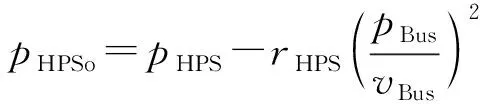
(8)
式中:pHPS为系统总载荷功率;pBus为系统直流母线功率。
为了实现直流母线电容内的能量EBus平滑输出,确保直流母线电压稳定,并获得总载荷电流期望轨迹。定义平滑输出变量y=EBus,控制变量u=pHPSo,ref,状态变量x=vBus,则由式(5)可知,状态变量x可表示为:

(9)
由式(5)至式(9)可知,控制输入变量u可表示为:
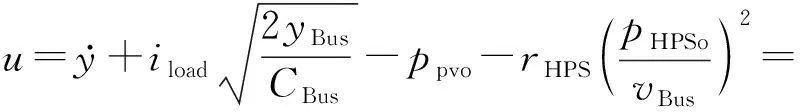
(10)
式(9)、式(10)为逆向动态方程,由式(9)、式(10)可知,状态变量x和输入变量u可由输出变量y及y的有限阶导数表示。根据非线性微分平滑理论,光储直流供电系统为微分平滑系统,则由式(10)可以看出系统总载荷参考功率pHPSo,ref可由y及其导数直接获得,避免了模型近似处理,控制精
度可确保。将获得的系统总载荷参考功率pHPSo,ref除以直流母线电压vBus即得到非近似处理的总载荷电流期望轨迹iHPS。
为稳定光—储—燃直流供电系统直流母线电压,利用式(5)将直流母线电压vBus与参考电压vBus,ref转换为电容能量EBus,设计反馈控制律为:
(11)
式中:K1和K2为控制器参数;yref为y的参考值。
由非线性微分平滑原理可知,采用式(11)所示的反馈控制律可在确保系统全局稳定的前提下,实现直流母线能量快速跟踪参考轨迹,平滑光伏输出功率,平稳直流母线电压,同时补偿模型参数偏差引起的跟踪偏差,进一步提升系统鲁棒性。
上层控制方法见附录A图A1,直流母线电压经过电压能量转换和反馈控制律,实现了直流母线电压平衡,并利用逆向动态方程实现非线性补偿,从而获得非近似处理的总载荷电流期望轨迹iHPS,并将其传输至下层控制器,实现系统的稳定协调控制。由式(11)可知,跟踪误差e=y-yref满足:
(12)
同时满足期望特征多项式:
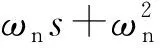
(13)
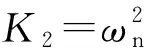
1.3 下层控制方法设计
为实现下层中光—储—燃系统间功率的协调控制,建立系统预测模型,如图1所示。当超级电容、蓄电池、燃料电池变换器的变压比保持不变且电流参考值平滑时,则超级电容、蓄电池、燃料电池变流器的动态行为可由受控电流源和变压器组成的简化动态系统表示,且由于电源内部内阻很小且电源端口呈现电压源特性,因此忽略电源内阻,将电源等效为大电容[29]。
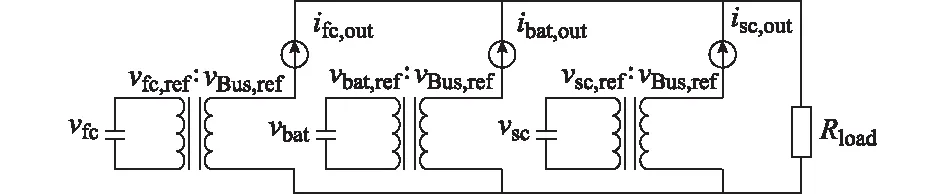
图1 超级电容/蓄电池/燃料电池动态行为模型Fig.1 Dynamic behavior model of super capacitor/battery/fuel cell
根据图1所示的简化动态系统,设计模型预测控制器。为满足所述的简化动态系统假设成立,将ilastfc,ref,ilastbat,ref,ilastsc,ref作为状态变量,以期电流参考值平滑;将vfc,vbat和vsc看成电源荷电状态(SOC)简单估计并作为状态变量,维持电源电压不变,保证系统持续稳定工作。为实现超级电容、蓄电池、燃料电池的功率协调分配,选择ifc,ref,ibat,ref,isc,ref作为控制变量。设置的状态向量、输出向量以及控制向量如式(14)至式(16)所示:
x=[vfcvbatvscilastfc,refilastbat,refilastsc,ref]T
(14)
u=[ifc,refibat,refisc,ref]T
(15)
y=[vfcvbatvscihpsdifcdibatdisc]T
(16)
式中:ifc,ref,ibat,ref,isc,ref分别为燃料电池、蓄电池和超级电容的参考电流;ilastfc,ref,ilastbat,ref,ilastsc,ref分别为上一时刻燃料电池、蓄电池和超级电容的电流采样值;difc,dibat,disc分别为燃料电池、蓄电池和超级电容的电流一阶微分量;iHPS为由上层控制获得的总载荷参考电流。
根据图1的动态行为模型和式(14)至式(16),可得离散控制模型:
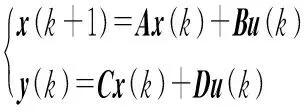
(17)
其中:A为状态矩阵;B为输入矩阵;C为输出矩阵;D为前馈矩阵。具体表达式见附录B。
为了使被控对象在控制器作用下未来N个时刻的输出预测值尽可能接近给定的期望值,同时抑制控制作用的剧烈变化。根据系统性能要求,结合状态预测模型,建立如下性能指标。
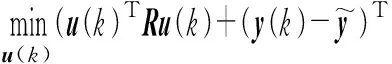
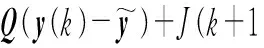
(18)
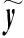
针对模型预测的无约束线性二次型最优控制问题,根据贝尔曼的动态规划法递推得到最优显式反馈控制律,实现闭环控制[30]。利用函数J(k,x)实施k到k+N的多阶段优化,其中k为当前时刻,N为预测步长。
假设J(k+1,x)的最终形式可由Pk+1,Vk+1,Zk+1表示:

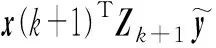
(19)
由贝尔曼递推方程可得如下线性离散系统最优控制问题的递推计算公式,由式(17)至式(19)可得一步预测最优控制表示为:
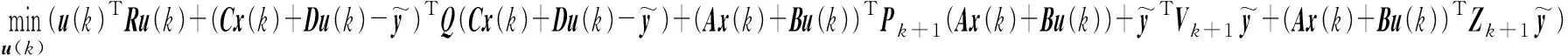
(20)
求解式(20)的黎卡提矩阵微分方程并令该方程为零,即:
(21)
得到一步最优控制函数uopt:

(22)
式中:K=(2R+2DTQD+2BTPk+1B)-1·(-2DTQC-2BTPk+1A),M=(2R+2DTQD+2BTPk+1B)-1(-2DTQ-BTZk+1)。
联立式(17)、式(20)和式(22)可得:
J(k,x)=x(k)T[KTRK+(C+DK)TQ(C+DK)+
(A+BK)TPk+1(A+BK)]x(k)+
x(k)T[2KTRM+2(C+DK)TQ(DM-I)+
(23)
式中:令KTRK+(C+DK)TQ(C+DK)+(A+BK)TPk+1(A+BK)=Pk+2,MTRM+(DM-I)T·Q(DM-I)+(BM)TPk+1(BM)=Vk+2,2KTRM+2(C+DK)TQ(DM-I)+(2A+BK)TPk+1BM+(A+BK)TZk+1=Zk+2。
由以上推导可知,N步最优控制函数uopt的参数K和M通过式(18)至式(23)更新递推得到。由式(18)可知,在采样时刻k,优化性能指标只覆盖k时刻起的未来有限时域N,随着时刻的推进,优化时域N同时向前滚动推移,在如式(18)所示的相对形式相同的性能指标下滚动优化,对在滚动的每一步以实时信息进行反馈校正,取代了传统最优控制中一次性的全局优化式,如式(22)所示。式(18)和式(22)表明预测控制中的优化不是一次离线进行,而是反复在线进行,避免了辨识最小化参数模型的困难,降低了在线优化的实时计算量,同时提高了控制系统的鲁棒性。
在采样时刻k,未来的控制量为u(k+m),m=0,1,…,N。将式(18)所示的有限时域性能指标作为该控制系统的李雅普诺夫函数,即
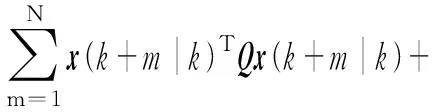
(24)
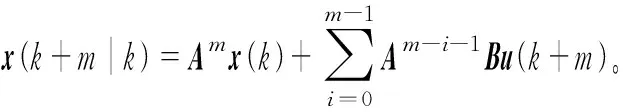
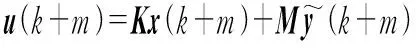
在采样时刻k+1,李雅普诺夫函数可表示为:
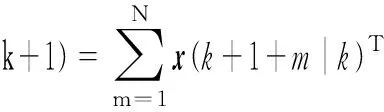
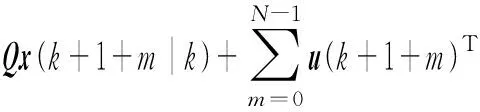
Ru(k+1+m)
(25)

在k+1时刻,由式(17)可以看出,k时刻的控制量可以作为k+1时刻的一个可行解虽不是最优解,因此可以将V(x(k+1),k+1)中的未来控制量序列u(k),u(k+1),…,u(k+N)向前移位并将序列中最后一个控制量替换为0,得到u(k+1),u(k+2),…,u(k+N-1),0的一个控制序列,则有:
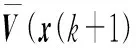
(26)
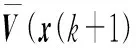
V(x(k+1),k+1)-V(x(k),k)≤
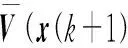
(27)
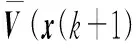
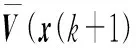
Qx(k+N|k)-x(k+1)TQx(k+1)-
u(k)TRu(k)
(28)
由终端约束的假设条件可知:
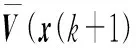
Qx(k+1)-u(k)TRu(k)
(29)
则李雅普诺夫函数的差为:
V(x(k+1),k+1)-V(x(k),k)≤-x(k+1)T·
Qx(k+1)-u(k)TRu(k)≤0
(30)
当满足终端约束条件时,根据李雅普诺夫第二法,该控制系统是渐进稳定的,适当选取Q和R可以改变系统渐进稳定的收敛速度。
针对各储能变流器,采用滞环控制使各电源电流值ifc,ibat,isc快速跟踪参考电流值ifc,ref,ibat,ref,isc,ref,下层控制方法如附录A图A1所示。
2 仿真验证
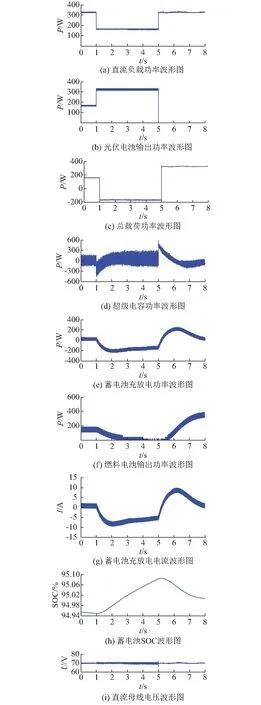
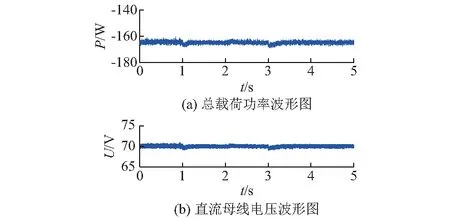
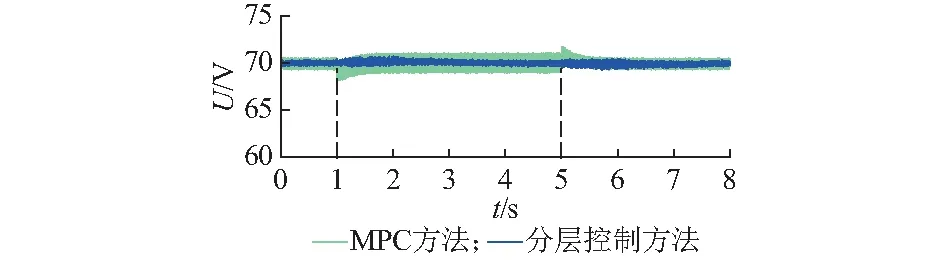
为了验证针对光—储—燃直流供电系统设计的控制方法的可行性和有效性,在MATLAB/Simulink环境下仿真负载功率变化,受云层影响光照急剧改变导致光伏电池输出功率变化以及系统参数发生摄动时,分析光伏输出功率平滑、直流母线电压稳定和各电源输出功率协调分配的情况。仿真中,光伏单元和蓄电池依据文献[27]建立模型,燃料电池依据文献[4]建立模型,超级电容采用一阶线性的串并联RC模型,由理想电容、等效串联内阻、等效并联漏电电阻构成。仿真时,燃料电池响应时间通常为3~7 s,输出功率Pfc仿真边界设置为:0 情形1:光伏输出功率与负载功率发生同向阶跃变化。图2(a)至图2(f)分别为负载功率、光伏输出功率、总载荷功率、超级电容充放电功率、储能电池充放电功率及燃料电池输出功率波形。图2(i)为直流母线电压动态响应波形。由图2(a)至图2(f)可知,在t=0~1 s的初始状态下,光伏输出功率为0,超级电容和蓄电池的放电功率为0,由燃料电池提供负载功率所需的326 W,由上层控制得到的期望的总载荷功率为163 W。 1)t=1 s时,光伏输出功率从0突增至326 W,同时负载需求功率从163 W突增至326 W,此时光伏输出功率等于负载需求功率。为了快速响应功率变化来协调各电源间的功率分配,由上层控制得到期望的总载荷功率为0,如图2(a)至图2(c)所示。t=1~5 s时,超级电容转入充电模式,承担系统响应的高频部分,吸收大于负载需求功率部分的突变功率。削减负载突变造成的对蓄电池以及燃料电池的冲击,提高系统的动态响应。为了维持超级电容的能量,确保系统稳定运行,超级电容逐渐释放本次吸收的功率,如图2(d)所示。由于蓄电池承担系统响应的低频部分,超级电容完成瞬态响应后,将由蓄电池吸收大于负载需求功率部分,并在t=2 s时达到最大充电功率,如图2(e)所示。由于此时蓄电池处于充电状态,相应的蓄电池SOC不断增加,如图2(g)和图2(h)所示。由于期间光伏输出功率等于负载功率所需,且燃料电池物理反应比蓄电池缓慢,燃料电池输出功率逐渐减小,并在t=4 s后与蓄电池充电功率降为零,此时,蓄电池SOC维持恒定不变,如图2(f)所示,系统进入稳态运行。 2)t=5 s时,光伏输出功率从326 W突减至163 W,负载功率从326 W突减至0,于是由上层控制得到期望的总载荷功率-163 W,此时光伏输出功率大于负载需求功率,燃料电池输出功率、蓄电池充放电功率和超级电容充放电功率都为零,如图2(a)至图2(c)所示。t=5~8 s时,超级电容转入充电模式,吸收大于负载需求功率部分的突变功率。超级电容完成瞬态响应后,将由蓄电池吸收大于负载需求功率部分,并在t=6 s时达到最大充电功率。此时蓄电池处于充电状态,因此相应的蓄电池SOC继续增加,如图2(g)和图2(h)所示。由于期间光伏输出功率大于负载功率所需,燃料电池输出功率保持为零。光伏输出功率持续为蓄电池进行充电,实现光伏储能,系统进入稳态运行。 仿真结果图2(c)和图2(i)表明:当系统发生光照及负载突变情况,上层控制快速响应功率变化,获得下层控制所需的期望总载荷功率,并通过下层控制协调各电源间的功率分配,使直流母线电压快速恢复平稳,始终保持在70 V,验证了基于微分平滑控制方法的正确性和可行性;仿真结果图2(d)至图2(f)表明:通过上层控制获得所需的载荷需求,根据各电源的充放电特性,由下层控制给出各电源不同充放电速率的电流参考值,实现了光伏输出功率等于负载需求功率、负载功率为零且光伏输出功率大于负载需求功率两种情况下各电源间功率的协调分配控制;仿真结果图2(e)、图2(g)和图2(h)表明:蓄电池在充放电速率约束条件下,响应快速,SOC平稳,与超级电容、燃料电池的有效配合,避免了反复充放电对电池的冲击,延长了使用寿命。 情形2:光伏输出功率与负载功率发生反方向阶跃变化。图3(a)至图3(f)分别为负载功率、光伏输出功率、总载荷功率、燃料电池输出功率、储能电池充放电功率和超级电容充放电功率。图3(i)为直流母线电压的动态响应波形图。由图3可知,在t=0~1 s时的初始状态,光伏输出功率为163 W,超级电容和蓄电池的充放电功率为0,燃料电池输出功率为163 W,由光伏电池与燃料电池提供负载需求功率的326 W,于是由上层控制得到的期望的总载荷功率为163 W。 图2 光-储-燃直流供电系统动态响应波形图(情形1)Fig.2 Dynamic response waveforms of photovoltaic-energy storage-fuel cell DC generation system (Case 1) 1)t=1 s时,光伏输出功率从163 W突增至326 W,同时负载需求功率从326 W突减至163 W。此时光伏输出功率大于负载需求功率,为了快速响应功率变化,从而协调各电源间的功率分配,由上层控制得到期望的总载荷功率0,如图3(a)至图3(c)所示。 2)t=1~5 s时,超级电容转入充电模式,吸收大于负载需求功率部分的突变功率。削减负载突变造成的对蓄电池以及燃料电池的冲击,提高系统的动态响应。超级电容为了维持本身能量,将逐渐释放本次吸收的功率,如图3(d)所示。超级电容完成瞬态响应后,蓄电池转为充电模式,吸收大于负载需求功率部分,并在t=2 s时达到最大充电功率,如图3(e)所示。此时蓄电池处于充电状态,因此相应的蓄电池SOC不断增加,如图3(g)和图3(h)所示。由于期间光伏输出功率大于负载所需功率,燃料电池输出功率逐渐为零,如图3(f)所示。光伏输出功率持续为蓄电池进行充电,实现光伏储能,系统进入稳态运行。 3)t=5 s时,光伏输出功率从326 W突减至0,负载功率从163 W突增至326 W,于是由上层控制得到期望的总载荷功率326 W。此时光伏输出功率小于负载需求功率,燃料电池、超级电容输出功率已达到零,蓄电池充电功率为326 W,如图3(a)至图3(c)所示。t=5~8 s时,超级电容转入放电模式,提供小于负载需求功率部分的突变功率。为了维持超级电容的能量,超级电容逐渐吸收本次释放的功率,如图3(d)所示。超级电容完成瞬态响应后,将由蓄电池提供负载需求功率不足部分,并在t=6 s时达到最大放电功率。由于蓄电池此时从充电状态开始转变为放电状态,因此相应的蓄电池SOC在充放电电流过零后开始减小,如图3(g)和图3(h)所示。由于期间光伏输出功率小于负载功率所需且燃料电池物理反应比蓄电池缓慢。t=8 s后,将由燃料电池提供负载需求功率,蓄电池放电功率达到零,蓄电池SOC将维持恒定不变,系统进入稳态运行。 仿真结果图3(c)和图3 (i)表明:当系统发生光照及负载相反方向突变的极端情况,上层控制快速响应功率变化,获得下层控制所需的期望总载荷功率,并通过下层控制协调各电源间的功率分配,使直流母线电压依然能够快速恢复平稳并保持在70 V,实现可靠供电;仿真结果图3(c)至图3(f)表明:下层控制实现了光伏输出功率大于负载需求功率,光伏输出功率为零且小于负载需求两种情况下各电源间功率的协调分配控制;仿真结果图3(e)、图3(g)和图3(h)表明:蓄电池充放电控制快速有效,当光伏出力不足且负荷需求增大时,能快速放电,补给需求缺口;当负荷锐减但光伏出力突增时,能快速充电,抑制母线能量富余引起的电压上升,分层控制方法通过控制蓄电池充放电速率,实现满足控制性能的同时,最大限度增加使用次数,延长蓄电池寿命。 图3 光-储-燃直流供电系统动态响应波形图(情形2)Fig.3 Dynamic response waveforms of photovoltaic-energy storage-fuel cell DC generation system (Case 2) 情形3:系统参数发生摄动。不考虑光伏以及负载变化,在t=1 s时,变流器并联静态损耗rHPS从0.18 Ω增大至0.36 Ω;在t=3 s时,蓄电池内阻值增大2倍,总载荷功率波形和直流母线电压波形分别如图4(a)和图4(b)所示。当变流器参数和蓄电池内阻发生突变时,微分平滑控制律通过补偿模型参数偏差,降低了控制系统性能受参数误差的影响,直流母线电压能够快速恢复至稳定状态;MPC通过滚动优化,对实时信息进行反馈校正,及时调整各电源的功率分配,使总载荷功率能够快速恢复平稳,验证了所提出的分层控制方法具有较高鲁棒性。 图4 光-储-燃直流供电系统动态响应波形图(情形3)Fig.4 Dynamic response waveforms of photovoltaic-energy storage-fuel cell DC generation system (Case 3) 情形4:性能对比分析。将论文所提出的分层控制方法与传统模型预测方法进行仿真对比。光伏输出功率为163 W,初始时负载为0,直流母线电压vBus为70 V,在t=1 s时负载需求功率突增至326 W,在t=5 s时负载需求功率恢复至0,仿真结果图5所示。当负载需求突增,直流母线电压发生暂降波动,通过控制动态调整各电源功率分配,快速恢复母线电压恒定。由图4可得,模型预测方法的调整时间ts=0.4 s,调整量σ=1.4%;基于微分平滑方法的分层控制调整时间很短,响应快速,并且能够实现零超调,量化性能比较如表1所示。由比较可知,论文所提出的分层控制具有良好的动、静态性能。 图5 负载阶跃变化下MPC与分层控制方法性能对比Fig.5 Performance comparison between MPC and hierarchical control during a load step 控制方法调整量σ/%调整时间ts/s稳态误差ess MPC1.40.400 分层控制00.120 本文对光—储—燃直流供电系统的稳定协调控制方法进行了研究,提出了一种能量管理分层控制方法。上层控设计微分平滑方法,获得下层控制所需非近似处理的总载荷电流期望轨迹,确保存在负载突变或光伏剧烈变化的情况下,系统依然能够快速跟踪期望轨迹,系统直流母线电压平稳;下层控制中设计模型预测方法,实现了光—储—燃系统间功率的协调控制。在MATLAB/Simulink环境下对光—储—燃直流供电系统分层控制方法的可行性与有效性进行了仿真验证,仿真结果如下。 1)当光伏电池输出功率或负载功率发生大幅阶跃变化时,可快速稳定直流母线电压,实现各电源间的协调控制,分层控制方法对外部扰动大幅变化具有较好稳定性;当变流器静态损耗以及蓄电池内阻发生突变时,系统依然能够保持平稳运行,分层控制方法对系统内部参数摄动具有较强鲁棒性;当负载需求发生突变,分层控制方法动态响应快速,无超调,跟踪无静差,静/动态性能优于传统MPC方法(调整时间ts=0.4 s、调整量σ=1.4%),具有更好的控制性能。 2)由非线性平滑微分控制与MPC结合的分层控制方法为可再生能源、混合储能装置、燃料电池等不同特性电源间的协调控制提供了简单可行的解决方案。但本文未对所提出的分层控制方法是否适用于光—储—燃系统结合风力发电、冷热电联供系统的交直流混合供电系统提出分析与论证,还需开展设计与测试工作,进一步将分层控制方法推广至结构更复杂的新能源发电系统是下一步研究工作的主要内容。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。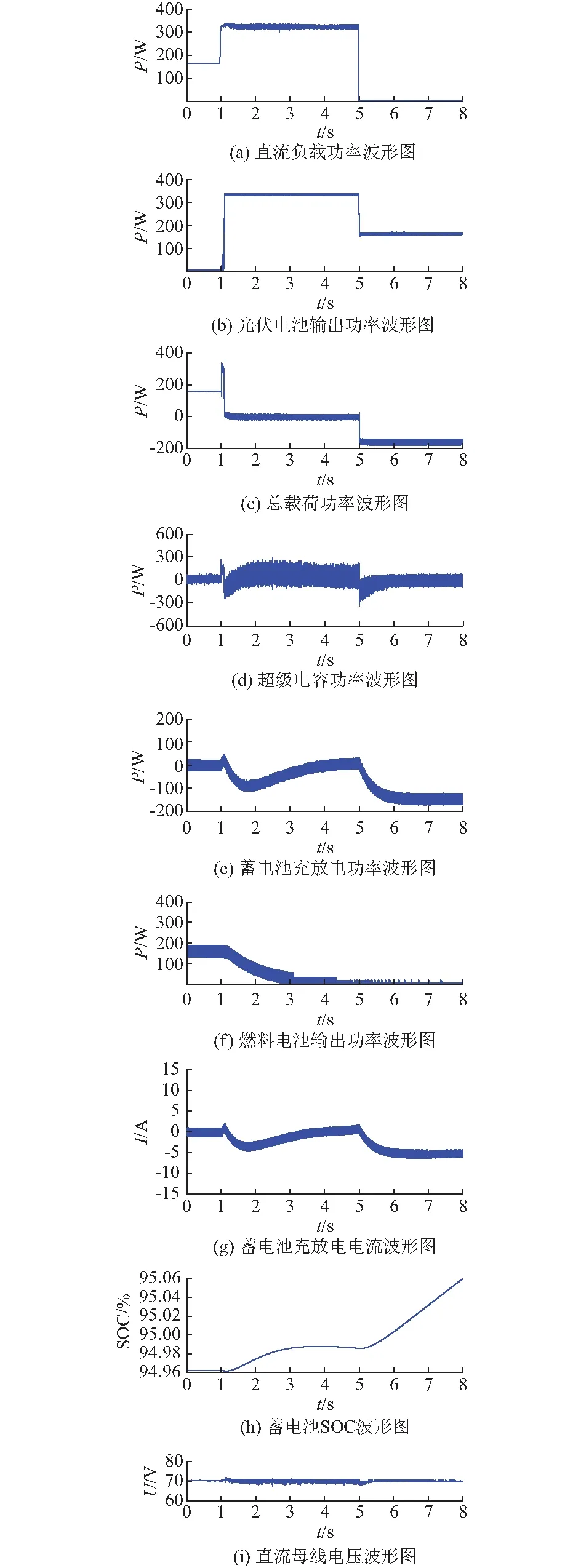

3 结语

