基于ANSYS的六自由度工业机器人静力学分析

（山西机电职业技术学院，长治 046011）

0 引言

工业生产中，六自由度机器人的应用非常普遍，工业机器人零部件的微小变形，会对机器人的精度产生影响，六自由度机器人的制造成本较高，开发周期较长，数值模拟能够极大缩短开发周期，同时找到更加合理的设计方案[1～3]。使用Pro/E软件确定机器人各个零部件的质量和相对位置，计算求得各个部分的载荷大小，在ANSYS中模拟，能够直观展现旋转座、摆动臂、摆动关节、旋转臂的应力和应变图[4,5]。

1 六自由度机器人模型建立

1.1 建立几何模型

六自由度机器人结构复杂，利用等效刚度代换理论，忽略线路、电位器、导线管等对计算结果影响不大的部件，将简化后的旋转座、摆动臂、摆动关节、旋转臂作刚性一体化处理[6～8]，得到机器人模型如图1所示。

1.2 定义模型材料及网格划分

六自由度机器人安装底座使用耐磨性好的HT 250灰铸铁，旋转座、摆动臂、摆动关节与旋转臂均采用线收缩小的ZL 108，材料属性如表1所示。使用ANSYS Workbench网格划分工具对旋转座、摆动臂、摆动关节、旋转臂分别进行网格划分，节点数和单元数如表2所示，网格划分情况如图2所示。

图1 六自由度工业机器人模型

图2 机器人零件网格划分结果

表1 机器人零件材料属性

表2 各零部件网格节点数与单元数

2 六自由度机器人零部件静力学分析

2.1 施加载荷

机器人的末端执行器在水平位置的位移量最大，选取该位置进行分析。由于自身重力，机器人各部分位置不同，受力也不同。以摆动关节为例，竖直方向受到机器人旋转臂和腕关节的作用，总质量为3.549kg，力的大小为49.490N，端面面积为0.003383m3，产生的压力为0.01463MPa，在Pro/E中测得力的作用点距离摆动臂端部沿臂展方向的距离为98.26mm，产生4863N·mm的力矩。各部分的受力大小如下表3所示。

表3 机器人零件载荷大小

2.2 应力分析

无预加载荷状态下，得到机器人零部件的应力分布云图3和应力大小表4。

图3 重力作用下的应力分布云图

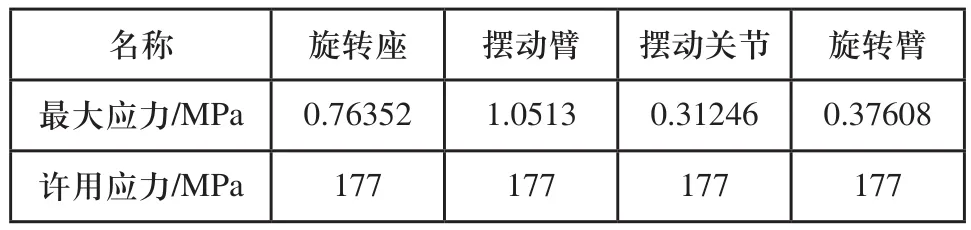
表4 重力作用下的应力大小

从图3和表4可以看出，在无荷重时，机器人零部件中，旋转座的最大应力为0.76352MPa，摆动臂的最大应力为1.0513MPa，摆动关节的最大应力为0.31246MPa，旋转臂的最大应力为0.37608MPa，摆动臂承受的应力最大，为1.0513MPa，危险位置在与旋转座连接处圆形端面的右侧边缘，摆动关节承受的应力最小。最大应力均远远小于ZL 108的许用应力。

2.3 应变分析

载荷和约束施加到摆动臂上后，进行求解，得到摆动臂无荷重下的总形变位移分布图4和应变大小表5。

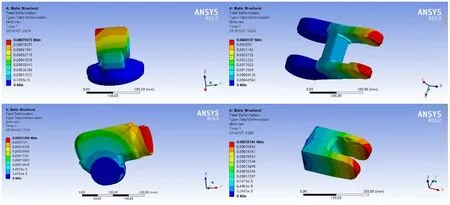
图4 重力作用下的总应变分布云图

表5 重力作用下的应变大小

从图4和表5可以看出，无荷重时，机器人旋转座的最大形变量为0.00079073mm，摆动臂的最大形变量为0.0040107mm，摆动关节的最大形变量为0.00031286 mm，旋转臂的形变量为0.00035741mm，相比之下，摆动臂的应变最大，对于机器人精度的影响更大，应变最大的位置在摆动臂右侧顶端。

3 结论

建立了六自由度工业机器人模型，使用Pro/E软件得到机器人模型各个部分的质量、质心、坐标数据，使用ANSYS对机器人进行静力学分析，获得了机器人旋转座、摆动臂、摆动关节、旋转臂的应力和应变的变化规律。结果表明，在无荷重时，机器人零部件中摆动臂承受的应力最大，为1.0513MPa，危险位置在与旋转座连接处圆形端面的右侧边缘，摆动关节承受的应力最小；无荷重时，六自由度机器人摆动臂的应变最大，为0.0040107mm，位于摆动臂右侧顶端。