二维重构数字微流控生物芯片的架构级布局设计及调度优化

（河南工程学院 机械工程学院，郑州 451191）

0 引言

由微机电系统和微电子流体系统组成的复合微系统已逐渐成为新型的系统芯片设计[1]。这些系统结合了微观结构和固态电子来集成多种能量域，如电、机械和流体等。微结构和微电子的结合使得新一代的集成系统瞄准了环境感应、生化分析、试剂检测以及精确流体分配等方面。而数字微流控芯片正属于这样的集成系统[2]。它的出现革新了生物化学和生物医学的诸多领域，使我们能够精准地控制少量流体用于精密分配，并能减少试剂消耗，以便进行在线生物化学分析、床边检测和实施过程监测[3,4]。

介电湿润是数字微流控技术中最常见的一种液滴驱动方式[5]。通过按次序地对电极施加电压，液滴可以自由地在2D数字微流控芯片上移动并到达任意位置，以完成相应的基本操作，如液滴分配、分离、混合和储存，具体结构如图1所示。虽然基于介电湿润的数字微流控技术非常适用于生化分析、临床诊断、食品安全和环境监测等领域，但这些都需要建立在系统级别的设计方法的基础上来实现的。

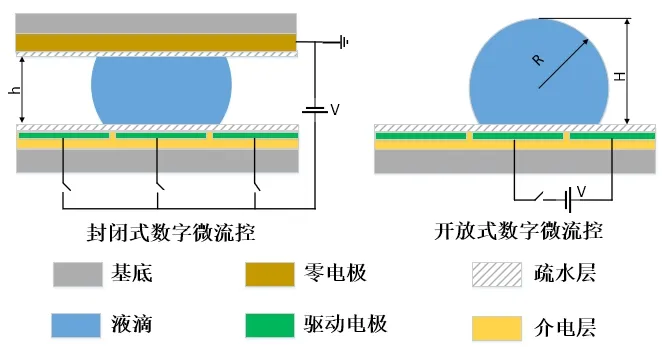
图1 数字微流控芯片结构

随着数字微流控生物芯片的应用越来越广泛，往往需要在同一个芯片上实现不同种类的生化分析操作的协同运作，这极大地增加了芯片的结构复杂性。传统数字微流控生物芯片所采用的全定制设计制作技术扩展性差，而且2D电极阵列的尺寸限制了片上并行操作的数量，同时，生化检验中各操作之间的功能依赖性在很大程度上也限制了操作的并行性。以上各种问题的出现使得传统数字微流控生物芯片的全定制设计技术已经远不适用于大规模的生化分析。因此，迫切需要计算机辅助设计来优化数字微流控生物芯片的结构，减少人为干预，提高芯片的利用率及效率[6～8]。现场可编程控门阵列[9]（field-programmable gate array, FPGA）是一种高密度的电子可编程逻辑器件，具有用户可重复定义的逻辑功能，即具有动态重构的特点。受数字微流控芯片本身尺寸的限制，为使其能够完成较为复杂的生化分析，数字微流控芯片需要具有动态重构特性，即在不同的时间范围内可以共用一块相同的微流控电极阵列区域以完成多种不同的任务。正是由于这一特性的存在，数字微流控芯片的阵列结构得以重新调整，以便满足不同的生化分析检验要求，进而降低芯片设计及使用成本，提高芯片使用效率，因此这一特性对于可重复使用的生物芯片来说至关重要。通过微控制器编程，可以在任意时刻独立地控制任一液滴在芯片上移动至指定位置，因此数字微流控生物芯片与FPGA在动态重构方面不仅具有许多相似之处，而且前者比后者具有更为显著的可编程能力。这是因为FPGA在互连以及逻辑块方面的可编程能力是受限的，而数字微流控电极阵列单元应该不仅可以用来储存液滴、完成相应的基本操作（如液滴输运、混合及分离等），而且片上的存储单元、液滴混合器和分离器可以随时创建、删除并重置，这会使我们能够创建极其灵活高效的生化分析系统。因此，如何利用计算机辅助设计来实现片上系统分区、资源配置以及调度是面向生化分析等应用的数字微流控芯片系统级设计亟需解决的一大问题。因此，受FPGA思想的启发，针对2D介电湿润的数字微流控生物芯片，本文提出了一种架构级结构布局综合设计优化算法用于解决资源受限的项目调度问题。

1 片上系统分区

实现数字微流控生物芯片的架构级布局综合设计的前提是对芯片电极阵列进行分区并生成分区图。所谓分区，就是对芯片电极阵列进行功能区域划分，不同区域用来完成不同的液滴操作。而分区图是一个虚拟地图，是片上不同功能区域（如混合区域，或称为混合器）随时序变化的位置，由设计者生成并预先加载到微控制器中，而每个液滴起点、终点以及两者间路径也被编程输入到微控制器中。微控制器可根据分区图按次序地为电极施加电压以驱动液滴在其对应的路径上完成相应的操作。图2显示了一个片上液滴存储区域，即存储器。其中一个单元格表示一个电极；蓝色代表该存储器储存的液滴，为避免其他液滴与该液滴发生不必要的混合，液滴之间应该至少相隔一个电极，因此深黑色方框内部区域属于隔离区域，将该液滴与其他液滴隔离，其他液滴只能沿图2所示点划线（通讯路径）在该液滴周围输运。该存储器只是数字微流控生物芯片上的一个分区。随着时间的延续，当有新的分区图被加载到微控制器中，该数字微流控芯片就会发生重构。图3显示了10×10数字微流控电极阵列的一种分区图，包含两个存储器、一个混合器、一个液滴加载区和一个废液回收区。

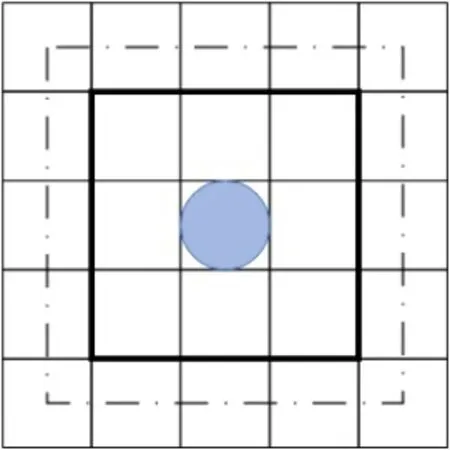
图2 片上液滴存储器

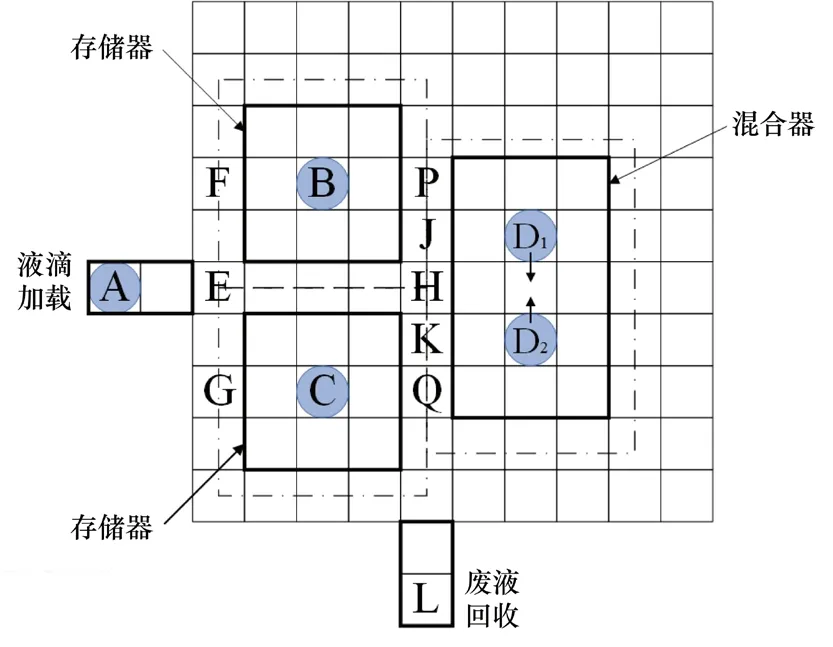
图3 分区图（含有两个存储器、一个混合器、一个液滴加载区和一个废液回收区）

在生化分析检验中，往往需要多个连续液滴完成相应的功能操作。如果几个连续液滴的路径不交叠，那么这些路径就被称之为兼容路径。液滴在兼容路径上的操作就可以并行进行；反之，如果路径不兼容，相应的液滴操作就必须依次进行。一个数字微流控芯片上的分区图不同，完成同一生化检验的时间也不同。因此，本文的目的在于在资源受限和操作依赖性的约束下，选择一种架构级布局设计方案，对检测操作进行调度并将其绑定到指定数量的片上资源上，最大限度地对这些检测操作进行并行处理，以最小化生化检验的完成时间。在液滴的所有基本操作中，液滴混合和分离操作耗时较长，而液滴输运耗时极短，在此忽略液滴输运时间，只考虑液滴加载、混合和分离时间。同时，我们将两个连续重构之间的时间跨度分割成多个相同长度的时隙。每个时隙的长度均等于一个生化检验中各操作所需时间的最大公约数。例如，如果液滴加载时间为2秒，液滴混合操作的时间为5秒，而液滴分离操作的时间为3秒的话，那么设置时隙大小为1秒。因此，液滴加载需要2个时隙，液滴混合需要5个时隙，液滴分离需要3个时隙。通过这种方式，我们将连续的液滴操作数字化，微控制器在每个时隙结束时会启动或完成某个操作。

2 构架级调度模型的建立

本文采用数据流图来表达数字微流控生物芯片上生化检测的调度问题，并建立该问题的数学模型。生化分析检验中每一步都可以用单个或一组基本液滴操作表示，而这样的一个基本操作对应数据流图中的一个节点。由节点u到节点v的有向边则表示与节点u和v相对应的操作之间的依赖关系，即与u对应的操作必须在与v对应的操作之前执行。图4给出了含有7个基本操作的数据流图，这7个操作分别是4个液滴加载操作和3个液滴混合操作。

图4 数据流图

生化检测调度问题可以看做是0-1整数线性规划问题，因此，具体分析过程如下所示：

设xi,j为二进制变量，则：

其中，1≤i≤N，N表示生化检验中的液滴操作总数（即数据流图中的节点数）；1≤j≤M，M表示松弛时间因子，即为所有操作时隙数量总和。由于每个检测操作只能被调度一次，因此：

操作i的开始时间Si可以用一个变量集{xi1, xi2,···,xim,}表示。假设每个时隙的长度为一个单位，那么操作i的开始时间为：

若操作i的持续时间为di，且操作i和i+1之间存在依赖关系，那么：

对于数字微流控生物芯片来说，除了上述的各操作间的依赖性这一约束以外，还有受芯片电极阵列尺寸限制的资源约束。假设nk为由分区图所确定的同一时隙内k型操作数量的最大值，则k型操作的资源约束表达为：

所谓生化检验操作调度优化的目标就是确定每一个检测操作的开始时间，以使所有操作的完成总时间达到最短。因此：

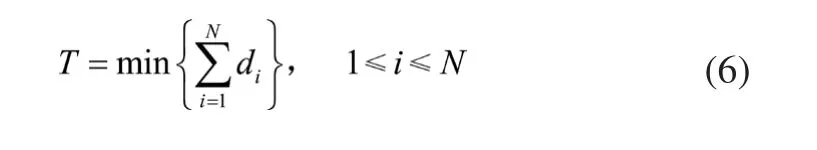
在最大限度地利用并行性来完成生化检测的基础上，上述优化目标可转化为最小化最后一组并行操作中持续时间最长的那个操作的完成时间。假设最后一组有l（1≤l≤N）个液滴操作并行执行，这l个操作中的持续时间最长的那个操作的完成时间为Tl，则优化目标转化为：

其中，nl表示最后一组基本操作数。

3 操作调度优化

以聚合酶链式反应（PCR）为例，研究数字微流控生物芯片的操作调度问题，并利用整数线性规划法来解决及优化该问题。

PCR主要包含8种样本试剂，分别为Tris-HCl、KCl、MgCl、明胶（gelatin）、三磷酸脱氧核苷酸混合液（dNTP）、引物、DNA模板以及Taq DNA聚合酶。PCR在数字微流控生物芯片上实施，要执行三大步骤，分别为样本试剂加载、样本混合（包含样本液滴输运、混合和分离三个基本操作）和样本混合物移出芯片以便完成后续加热操作，其具体实施步骤如下所示：

1）加入Tris-HCl；2）加入KCl，并与Tris-HCl充分混合；3）加入MgCl，并至充分混合；4）加入明胶，并至充分混合；5）三磷酸脱氧核苷酸混合液（dNTP），并至充分混合；6）加入引物，并至充分混合；7）加入DNA模板，并至充分混合；8）加入Taq DNA聚合酶，并至充分混合。

如果图3即为实施PCR的数字微流控生物芯片的分区图的话，其对应的数据流图如图5所示。

图5 与图3分区图对应的数据流图

这里假设液滴加载操作和液滴混合操作的完成时间分别为2秒和6秒，而液滴输运时间极短，忽略不计。因此，一个单位时隙长度即为2秒。注意，通常在生化检验中，液滴混合操作之后往往都要进行液滴分离操作，因此这里液滴混合操作的完成时间已包含液滴分离操作的时间。根据图3所示的分区图以及图5数据流图中所表达的各操作之间的依赖性，可以得到与之对应的操作调度方案，如表1所示。从图3中可以定义7条基本操作路径，分别为：1）路径1：A-E-H-J-D1；2）路径2：A-EH-K-D2；3）路径3：A-E-F-B；4）路径4：A-E-G-C；5）路径5：B-P-J-H-K-D2；6）路径6：C-Q-K-D2；7）路径7：D2-K-Q-L。

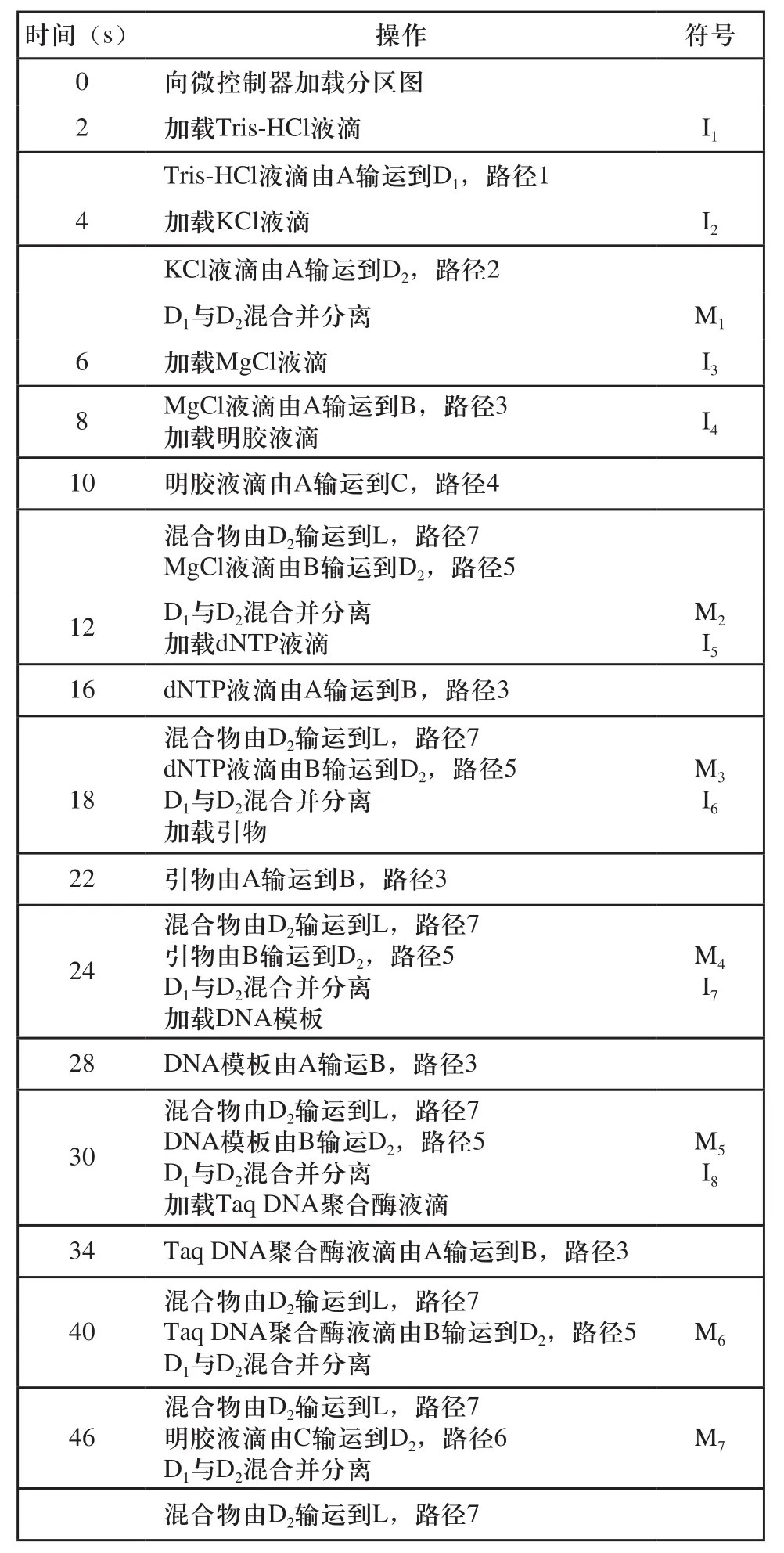
表1 基于图3和图5（1个混合器）的PCR操作调度方案1

表1中各时间表示从第一步开始到所在步骤完成时所消耗的时间。根据图3分区图以及图5数据流图，表1得到的PCR反应操作调度方案1的完成时间为46s，而总操作数为15个，包含8个样本加载操作和7个液滴混合操作。对应的一个单位时隙长度为2秒，因此，需要23个时隙用于该PCR操作调度方案的完成。那么，该方案对应的整数线性规划模型将x1,j，x2,j，…，x15,j来表示决策变量，其中j=1,2,…,23。因此，15个操作的开始时间分别为：

另外，根据图5数据流图中各操作之间的依赖关系，应有：

其中，d1=d2=…d8=2s，d9=d10=…d15=6s。

这种操作调度方案对应的资源约束表达为：

图6 两个混合器的分区图

图7 图6分区图对应的数据流图

图8 三个混合器的分区图

为了优化操作调度方案，重新生成两个分区图（如图6和图8所示），分别带有两个和三个液滴混合器，图7表示与图6含有两个液滴混合器的分区图相对应的数据流图。根据图6和图7，得到与其对应的PCR反应操作调度方案2，如表2所示，其对应的液滴输运路径分别为：1）路径1：A-E-P-Q-J-D1；2）路径2：A-E-P-Q-K-D2；3）路径3：A-E-F-B1；4）路径4：A-E-G-B2；5）路径5：B1-J-K-D2；6）路径6：B2-K-Q-L；7）路径7：D2-KQ-L。

由表2可知，利用两个液滴混合器来实施PCR反应所需完成时间只有32s，与调度方案1相比，完成时间缩短了30.4%。同样方法分析图8带有三个液滴混合器的分区图，可得PCR反应的完成时间也是32s，因此，对于10×10的数字微流控电极阵列来说，两个液滴混合器已经可以实现PCR反应中最大程度的并行性，完成时间也达到最短。

4 结论

针对二维数字微流控生物芯片，本文提出了一种架构级结构布局设计以及操作调度优化方案。采用与FPGA类似的方法，对芯片进行系统分区、资源配置以及操作调度。利用0～1整数线性规划法建立生化检验模型，通过将不同的系统分区图输入微控制器，自动且最大程度地实现了并行性，大大缩短了生化检验的完成时间，优化了聚合酶链式反应操作调度方案。

表2 基于图6和图7（两个混合器）的PCR操作调度方案2