概率问题中的典型错例剖析

魏玉春

概率是描述一类事件发生可能性大小的数学模型，也是近几年中考的必考知识点.在学习过程中，许多同学因为对概念把握不准确，对原理理解不透彻等造成种种错误.我们现结合下面的例子对几种常见错误进行归类剖析，以引起大家的注意，希望对同学们今后的学习有所启迪与帮助.

一、对概率的意义理解不透

例1 小丽抛掷一枚硬币10次，有7次正面朝上，当她抛第十一次时，正面朝上的概率是_______.

【错解】

【剖析】造成错误的原因是没有真正理解概率的意义，把概率与频率混为一谈.概率与频率是两个不同的概念，但两者又具有十分密切的关系.当重复试验次数足够多时，频率会趋向于稳定，此时稳定的频率与概率十分接近，所以概率的大小可以通过大数次试验得到的稳定频率去估计.本例中因为试验次数太少，所以不能把频率作为概率的估计值.

抛掷一枚硬币时，因为每次试验都有两种等可能的结果，即正面朝上或反面朝上，故当小丽抛第十一次时，正面朝上的概率是-

【正解】-

二、对概率计算公式的错误使用

例2 学校新开设了航模、彩绘、泥塑3个社团，如果征征、舟舟两名同学每人随机选择参加其中一个社团，那么征征和舟舟都选到航模社团的概率是（ ）.

【错解】B.

【剖析】错解者错误地认为，从航模、彩绘、泥塑3个社团中，随机选择一个社团，征征和舟舟每人选到航模社团的概率都是，所以他们都选到航模社团的概率是现这种错误想法的根本原因是对等可能条件下概率的计算公式模糊不清.

用树状图分析如下：

由上图可得，共有9种等可能的结果，其中征征和舟舟都选到航模社团的结果只有1种，所以征征和舟舟都选到航模社团的概率是.

【正解】C.

三、对事件等可能性认识不清

例3 一个家庭有3个孩子，求这个家庭有2个男孩和1个女孩的概率.

【错解】这个家庭中3个孩子的性别共有4种情况：男、男、男；男、男、女；男、女、女；女、女、女.所以P（有2个男孩和1个女孩）=.

【剖析】这是初学概率的人最容易犯的错误.虽然这个家庭中3个孩子的性别情况只有上述4种，但每一种情况出现的可能性并不相同.错解者忽略了概率的等可能性这个重要特征.

【正解】画树状图如下：

∵共有8种等可能的结果，而是2个男孩和1个女孩的结果有3种.

四、对事件的结果考虑不周

例4 3张外观相同的卡片上分别标有数字1，2，3，从中随机一次抽出两张，这两张卡片上的数字恰好都小于3的概率是多少？

【错解】画树状图如下：

∵共有9种等可能的结果，而两张卡片上的数字恰好都小于3的结果有4种，

【剖析】导致本题求解错误的原因是审题不清，忽略了问题中一个重要条件“从中随机一次抽出两张”，在此条件下进行试验，最后的结果中不可能出现两张卡片上的数字完全相同的情况.

【正解】画树状图如下：

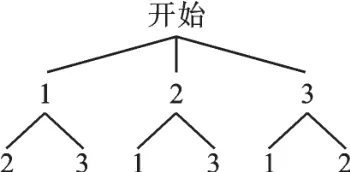
∵共有6种等可能的结果，而两张卡片上的数字恰好都小于3的结果有2种，