方差与数据的稳定性

马兆兵

苏科版《数学》九年级上册117页的第3题是这样描述的：

要从甲、乙两名运动员中选出一名参加校际100m比赛，对这两名运动员进行了10次测试，成绩如下（单位：s）：

12.9 12.8 12.8 12.9 13.0 12.9 12.9 13.1 12.9 12.8甲乙12.8 12.9 12.9 12.7 13.2 13.1 12.8 13.0 12.7 12.9

根据测试成绩，你认为选派哪一名运动员参赛更好些？为什么？

两名运动员的平均成绩都是12.9s，此时可通过计算两组数据的方差来比较他们的稳定性.甲的方差为0.024，乙的方差为0.008，则选择乙参加比赛.显然，方差刻画一组数据的离散程度（稳定性）.

一、用方差判断一组数据的稳定性

例1甲、乙两种水稻试验品种连续5年的平均单位面积产量如下（单位：吨/公顷）：

9.4 10.3 10.8 9.7 9.8品种年数甲乙第一年第二年第三年第四年第五年9.8 9.9 10.1 10 10.2

经计算，x甲=10吨/公顷，x乙=10吨/公顷，试根据这组数据估计________种水稻品种的产量比较稳定.

【解析】甲种水稻产量的方差是：

乙种水稻产量的方差是：

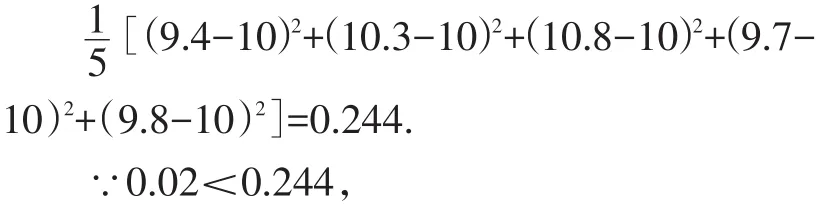
∴甲种水稻品种的产量比较稳定.

【点评】1.比较两组数据的稳定性的步骤：

（1）计算这两组数据的平均数.

（2）分别计算各自方差：s2=［（x1-x）2+（x2-x）2+…+（xn-x）2］.

（3）一组数据的方差越大，说明这组数据的离散程度越大；一组数据的方差越小，说明这组数据的离散程度越小.

2.比较一组数据的稳定性需要注意的问题：

一般情况下，两组数据只有在平均数相同的情况下才根据方差的大小确定它们的离散程度.

二、利用图表解决数据稳定性的问题

例2 为了从甲、乙两名选手中选拔一人参加射击比赛，现对他们进行一次测验，两个人在相同条件下各射靶10次，为了比较两人的成绩，制作了如下统计图表：

甲、乙两人的射击成绩统计表

（1）请补全上述图表（请直接在表中填空和补全折线图）.

（2）如果规定成绩较稳定者胜出，你认为谁应胜出？说明你的理由.

（3）如果希望（2）中的另一名选手胜出，根据图表中的信息，应该制定怎样的评判规则？为什么？

【解析】（1）根据折线统计图，得甲的射击成绩为（去掉第八次的成绩）9，6，7，6，2，7，7，8，9，平均数为7环.

则甲第八次射击成绩为：

70-（9+6+7+6+2+7+7+8+9）=9（环），

从小到大排列甲的成绩为：2，6，6，7，7，7，8，9，9，9，中位数为7环.

甲成绩的方差为：

乙的射击成绩为：2，4，6，8，7，7，8，9，9，10，则平均数为：

乙成绩的方差为：

补全表格和折线图如下：

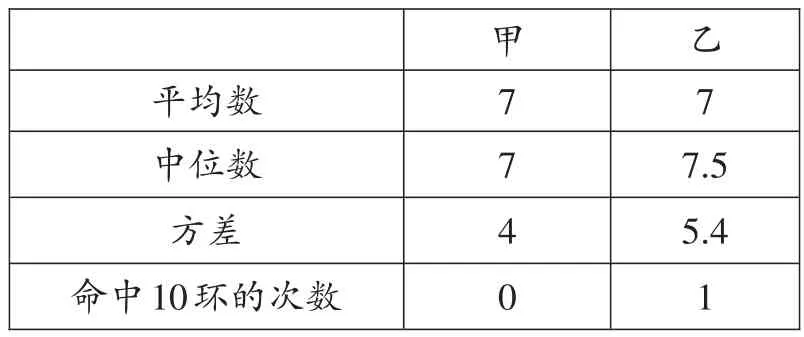
甲、乙两人的射击成绩统计表

（2）甲应胜出.理由：由于甲的方差小于乙的方差，故甲成绩较稳定，甲应胜出.

（3）若希望乙胜出，可以制定规则为：命中10环的总次数多的胜出.

理由：因为甲命中10环的次数为0，而乙命中10环的次数为1.

【点评】利用图表解决数据稳定性的问题注意：

1.从图表中获取正确的数据.

2.计算各组数据的平均数、方差.

3.比较大小，确定其稳定性.

三、方差的性质

例3 若一组数据a1，a2，a3的平均数为4，方差为3，那么数据a1+2，a2+2，a3+2的平均数和方差分别是（ ）.

A.4，3 B.6，3 C.3，4 D.6，5

【解析】∵数据a1，a2，a3的平均数为4，

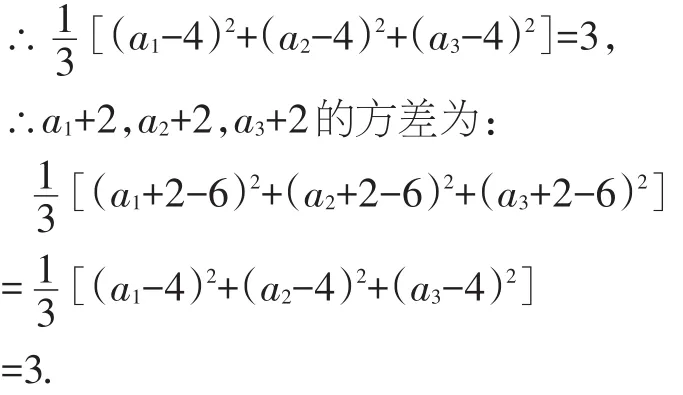
∴数据a1+2，a2+2，a3+2的平均数是6.

∵数据a1，a2，a3的方差为3，

故选：B.

【点评】一组数据x1，x2，x3，…，xn的平均数、方差之间的关系如下：

一组数据方差s2 s2表示形式平均数x x+a x1，x2，x3，…，xn（x1+a），（x2+a），（x3+a），…，（xn+a）kx1，kx2，kx3，…，kxn（kx1+a），（kx2+a），（kx3+a），…，（kxn+a）kx k2s2 kx+a k2s2