非下采样Shearlet域多变量模型的图像去噪

刘巧红，林 敏，李广超

(1.上海健康医学院医疗器械学院， 上海 201318; 2.上海光华中西医结合医院， 上海 200052;3.同济大学电子与信息工程学院， 上海 200092)

图像去噪在图像处理领域是一个既基础又富有挑战性的课题，受到了长期关注和广泛探讨。自统一的小波分析数学理论建立后，由于其良好的时频特性及稀疏表示能力，以小波变换为基础的去噪研究掀起了一股热潮。研究表明，图像信号和噪声信号在小波域表现出截然不同的分布规律。Donoho等[1]基于这一特点，开创性地提出了小波硬阈值收缩法，并取得了良好的去噪效果。随后提出的软阈值收缩法[2]、自适应阈值收缩法[3]、双变量收缩法[4]及基于无偏估计的收缩法[5]等继续沿用这一思想，将含噪图像经小波变换后的系数进行一定收缩，从而估计原始图像的系数，重构后获得去噪图像；然而，小波变换具备的良好点奇异性，不足以最优地表示图像中广泛存在的边缘和纹理等高维信息，同时小波变换还缺乏方向选择灵活性和各向异性。为克服小波变换的缺陷，一种基于合成膨胀的仿射系统构造的Shearlet变换被提出，其优越的方向选择性和各向异性，良好的多分辨性等特性使得其可以对图像进行灵活地分解，并对图像中的边缘和纹理等细节信息提供最优的稀疏表示[6]；然而Shearlet变换过程中包含下采样操作，缺乏平移不变性[7]，去噪图像中易出现伪吉布斯现象，导致图像效果失真。此后，Easley等[8]提出了非下采样剪切波变换(non-subsampled shearlet transform, NSST)，详细分析了NSST的结构设计和实现原理，采用了硬阈值对NSST系数进行收缩处理，达到了图像去噪的目的。NSST作为一种具有平移不变性的Shearlet变换，在保持了标准Shearlet变换原有优势的同时，克服了伪吉布斯现象，更加适合于图像去噪；然而，NSST域硬阈值收缩去噪将Shearlet系数视为单独的个体，缺乏系数之间相关性的考虑。为充分利用Shearlet系数的相关性，进一步提高去噪性能，本文提出了基于最大后验估计的NSST域多变量收缩模型，该模型充分利用了NSST域尺度内和尺度间邻域系数的相关性，在贝叶斯理论框架下，利用MAP估计推导出多变量收缩函数，估计出原始图像的NSST系数，并结合硬阈值收缩最高尺度NSST系数，最后经NSST逆变换得到最终的去噪图像。通过与几种经典去噪方法的比较，本文方法在有效地去除噪声的同时，克服了伪吉布斯效应，很好地保留了图像的边缘和细节信息。

1 非下采样剪切波变换(NSST)

Shearlet是在合成小波理论的基础上发展起来的多尺度变换工具。它通过特殊形式的具有合成膨胀的仿射系统构造，是一种接近最优的多维函数稀疏表示方法。Shearlet具有简单的数学结构，可以通过对基本函数的膨胀、剪切和平移变换来构造。当维数n=2时，其合成膨胀的仿射系统定义为

(1)

式中：ψ∈L2(R2)；A和B是2×2的可逆矩阵，A表示各向异性膨胀矩阵，控制其尺度，B表示剪切矩阵，控制其方向，且|detB|=1。若对于L2(R2)，AAB(ψ)满足Parseval框架，则称该系统为合成小波。

在频域中，Shearlet的几何性质更加直观，不同尺度的剪切波ψj,l,k在其频域支撑下，表现为近似大小为22j×2j,沿着斜率l2-j的直线且关于原点对称的梯形区域，如图1所示。Shearlet基函数的支撑区域可以随着尺度的长宽比发生变化，因此能够最优地表示图像的内在几何结构。然而，Shearlet在变换的过程中，在图像分解时进行了下采样操作，使得Shearlet系数冗余度较低，从而缺乏平移不变性，将其应用于图像去噪时易产生伪吉布斯现象。为克服这一缺陷，非下采样Shearlet变换舍弃了传统Shearlet的下采样操作，通过非下采样金字塔组和非下采样滤波器组合分解，获得与原始图像大小相同的一系列子带图像，增加了图像系数的冗余度并使该变换具备平移不变性，更加适合图像去噪。

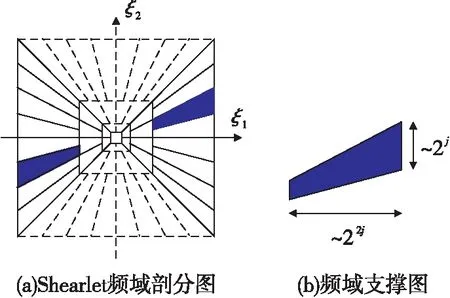
图1 Shearlet频域剖分和支撑图

2 基于NSST的多变量收缩模型的图像去噪算法

2.1 NSST域多变量收缩模型

早期小波域的软硬阈值去噪方法是以小波系数的独立性为基础，此后Sendur等[4]挖掘出图像经小波变换后的尺度间相应位置系数具有强烈的依赖关系这一重要性质，利用非高斯密度函数对父子系数分布进行统计建模，在贝叶斯统计理论框架下得出了双变量收缩函数用于图像去噪，可取得优于基于小波系数独立性去噪方法的效果。双变量收缩函数仅考虑了尺度间父子系数之间的依赖关系，而Sendur等进一步研究发现小波系数尺度内的邻域系数之间同样存在着依赖关系，随后扩展出包含小波系数尺度间和尺度内依赖关系的多变量收缩模型。双变量收缩模型和多变量收缩模型被推广到多尺度变换域下，众多的去噪实验结果进一步验证了这2种模型的适用性和高效性[9-11]。

非下采样剪切波具有良好的方向选择性和平移不变性，以及接近最优的稀疏表示能力，同时NSST系数也存在着类似小波系数的相关性，利用这种相关性可以更好地估计原始的NSST系数，从而提高图像去噪性能；因此，本文提出了基于NSST域目标系数及其父系数、邻域系数关系的多变量模型。

设yo,yp和yn为含噪图像的NSST系数，yo为目标系数，yp为yo的父系数，yn(n=1,2,…,k)为yo的邻域系数；uo,up和un(n=1,2,…,k)为清晰图像相应位置的NSST系数；vo,vp和vn(n=1,2,…,k)为零均值高斯噪声系数，则有：

(2)

令y=(yo,yp,y1,y2,…,yk),u=(uo,up,u1,u2,…,uk),v=(vo,vp,v1,v2,…,vk)，则式(2)等价为

y=u+v。

(3)

根据贝叶斯定理，已知含噪NSST系数y的情况下，原始图像的NSST系数u的MAP估计为

(4)

由式(4)可知，能够准确估计原始图像NSST系数的前提是确定关于u的概率密度函数pu(u)和v的概率密度函数pv(v)。假设噪声是零均值的高斯白噪声，噪声系数则服从高斯分布，式(4)中的噪声系数概率密度函数为多变量高斯密度函数，即

(5)

将式(5)代入式(4)，得到

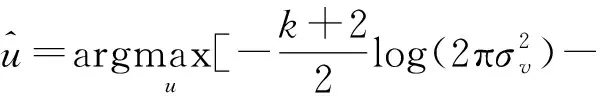
(6)

令f(u)=log(pu(u))，由于f(u)是严格凸且可微的，因此式(6)关于u的偏导为

(7)

自然图像的小波系数边缘密度满足一种“尖峰重尾”的非高斯分布，常采用广义高斯分布模型、高斯混合模型以及拉普拉斯模型等来描述这种分布特性；然而，这些模型仅仅考虑小波系数在同一尺度内的依赖关系，未能将不同尺度间的系数依赖关系刻画进去。为此，本文引入多变量概率密度函数

(8)

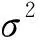
将式(8)代入式(7)，得到方程组：

由方程组(9)可以推出

(10)

进一步由式(10)得到

(11)

其中，(g)+定义为：

将式(11)代入式(9)中的第一个方程式，得到

(12)

ys=us+vs。

(13)

由于us和vs之间相互独立，则有

(14)

(15)

(16)

根据式(16)可知，图像经过NSST分解后的每个子带的系数边缘方差不同，本文中目标NSST系数的标准差由式(17)经验性地估计。

(17)

式中：W选取的是大小为7×7的矩形窗口；N2为该窗口内的NSST系数个数。自适应参数β由最小二乘法拟合确定，本文选取去噪性能最佳时的值，即β=0.05。

含噪图像经过NSST分解后,得到一个低频子带图像和一系列的高频子带图像。低频子带集中了原始图像大部分的能量,而噪声则主要分布在各个高频子带中。本文提出的多变量函数收缩去噪是基于NSST系数的尺度间的父子关系和尺度内的邻域关系实现的，然而，含噪图像经多次分解后最高尺度的NSST系数缺乏父系数，无法利用尺度间的父子关系达到去噪目的；因此，针对最高尺度的高频子带，本文结合式(18)的硬阈值去噪方法进行处理。

(18)

2.2 去噪算法流程

基于NSST的多变量收缩函数的图像去噪算法步骤如下。

1) 将含噪图像进行NSST变换，得到一个低频子带图像和一系列的带通方向子带图像；

3) 对经NSST分解得到的除最高尺度之外的带通方向子带，利用提出的多变量收缩函数式(12)估计出相应的原始NSST系数；

4) 对经NSST分解得到的最高尺度带通方向子带，利用式(18)的硬阈值收缩函数估计出相应的原始NSST系数；

5) 由所有估计出的带通方向子带系数和低频子带系数做NSST逆变换，得到最终的去噪图像。

3 实验结果与分析

为了验证本文提出的去噪方法的有效性，选取了大小均为512×512的Lena、Barbara和Peppers 3张具有代表性的标准测试灰度图像进行去噪实验，在每张图像上叠加不同强度的零均值的高斯白噪声，并与经典去噪算法BiShrink[4]、SURE_LET[5]、BLS_GSM[12]、ROF_FORDA[13]和ITGV[14]进行比较。含噪图像由NSST进行4级分解，每级的分解方向数分别为8、8、16、16。采用峰值信噪比(PSNR)来衡量不同方法的图像去噪性能，噪声图像经各种方法去噪后的PSNR值，如表1所示。可见，本文方法取得了相对较高的PSNR值。图2是利用各种方法对噪声方差为20的Lena图像的去噪结果比较。从视觉效果上可以看出：BiShrink方法整体去噪质量相对较差，图像清晰度较低；SURE_LET方法在图像平滑区域的噪声抑制不够彻底，仍有噪声残留；BLS_GSM方法在图像的梯度变化较大处伴有伪影和少量划痕；ROF_FORDA方法是利用一阶原始对偶算法求解经典的ROF模型实现去噪，难以避免地出现阶梯效应；ITGV方法的优点是克服阶梯效应，纹理部分相对保护不足；本文方法在有效地去除噪声的同时，较好地保持了边缘和纹理等细节信息，并且几乎不存在伪影现象，总体视觉效果优于其他几种方法。

实际应用中，核磁共振成像(magnetic resonance imaging, MRI)图像的形成过程中由于硬件电路和监测对象等多种原因会引入噪声，噪声降低了MRI图像的质量，从而影响了医生对疾病的诊断以及科研人员对疾病的研究；因此，去噪是提高MRI图像质量的关键预处理步骤。为验证本文方法的实用价值，选取了医学MRI图像作为测试样本，在原始图像上添加了噪声方差为30的高斯白噪声。图3是各种方法的去噪结果比较。从视觉效果上，本文方法有显著改善。

表1 各种去噪方法的PSNR值比较结果

图2 Lena图像的去噪结果比较

图3 MRI图像的去噪结果比较

4 讨论

综上所述，本文方法无论是在客观指标上，还是主观视觉效果上都取得了优越的去噪性能，其主要原因有以下几点。

1)从结构上来看，Shearlet变换是多尺度几何分析工具，具有灵活的方向敏感特性及良好的时频局部特性，是一种接近最优的多维函数稀疏表示方法。对于二维信号，其不仅能识别所有的奇异点，也能跟踪奇异性相关的几何信息，如奇异性的方向等，从而更加准确地描述图像中的线状奇异性，这是小波变换所缺乏的特性。

2)非下采样Shearlet作为标准的Shearlet变换的扩展，执行过程中采用了非正交变换，避免了下采样操作，变换后各个尺度上的每个方向子带具有与原始图像相同的大小，提高了图像的冗余度，从而使得NSST具有平移不变性，克服了去噪时奇异点附近易于产生伪吉布斯现象的缺陷。

3)NSST域的多变量收缩模型的建立充分考虑了当前系数与其相邻子带父系数及领域系数之间具有的强烈依赖关系，对比于仅考虑当前系数的阈值收缩方法，其去噪效果更佳。

4)针对NSST变换后产生的一系列高频方向子带中最高尺度子带不存在父系数的问题，结合硬阈值的方法进行收缩去噪，保证所有高频子带具有相应的处理，进一步提高了去噪性能。

5 结论

针对去除图像中的噪声污染问题，本文提出一种基于NSST域的多变量收缩去噪方法。它充分利用NSST作为一种多尺度变换工具，具有的平移不变性和良好方向选择性等优势和经NSST分解后得到的带通方向子带系数在尺度内及尺度间的邻域系数相互依赖关系，在进行收缩去噪的同时，有效地保护了图像中的边缘及纹理细节，呈现出良好的视觉效果。与BLS_GSM、SURE_LET以及ProShrink等经典去噪方法相比较，峰值信噪比有着明显的改善。需要说明的是，本文方法的计算复杂度需要进一步的提高。