认识向量,亲近向量
徐树旺


向量是近代数学中重要和基本的数学概念之一,是沟通代数、几何与三角函數的一种工具,有着极其丰富的实际背景,在数学和物理学科中具有广泛的应用.向量内容已成为高中数学课程的“核心概念”之一.
一、向量体现了数学与物理的天然联系
生活中的向量随处可见:“风力3级,风向东北”、“飞机每小时向西北方向飞行900km”、“用了300kg的力向上提一物体”等,向量最初被应用于物理学,很多物理量如位移、速度、加速度、力等都是向量的原型,
如,两接连的位移确定一个新位移——向量的加法(α十b)的原型(图1);力所做的功是由力与位移两矢量(物理上矢量——既有大小、又有方向、又有作用点)唯一确定的一个数——向量的数量积(α·b)的原型(图2).
“向量”一词来自力学、解析几何中的有向线段,英国大科学家牛顿使用有向线段表示向量,将向量与力学应用结合在一起.笛卡儿坐标(x,y)形式的出现,使向量为力学应用提供了一种有效的数学工具.
二、向量代数“身份”的核心内容是运算
运算是数学学习中的一个基本内容,从小学开始,运算对象不断扩展:从整数到分数、从正数到负数、从有理数到实数;从数到字母,再到多项式等;数运算、字母和多项式运算,这些都是数学中的基本运算.
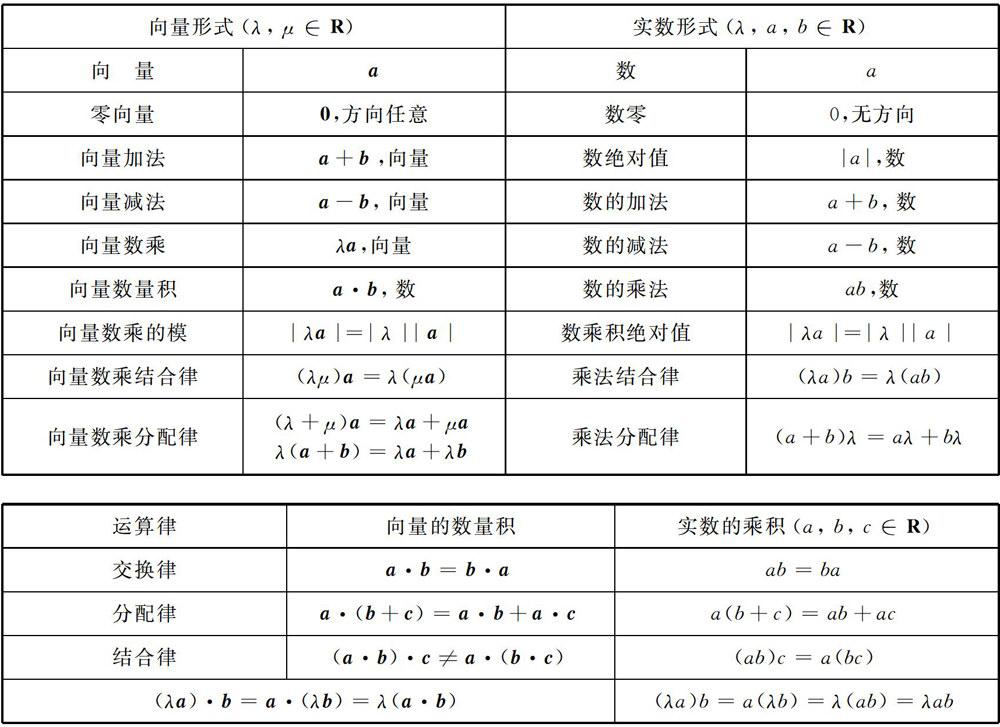
向量具有代数形式与几何形式的“双重身份”,既是代数的对象,又是几何的对象.作为代数对象的向量,必有运算法则和运算律,可与实数进行类比.
实数的运算结果始终是数,α十b,α-b,λα运算结果仍是向量,而向量的数量积(点乘)运算结果不是向量了.如果说从数的运算到字母的运算是运算的一次飞跃,那么运算对象扩展到向量则是运算认识上又一次飞跃.
三、向量是解决几何问题的重要工具
向量是既有大小、又有方向的量,是通过代数运算刻画几何对象及其位置关系、几何度量问题的工具.
解法1中,建立坐标系,将几何问题代数化(可以是三角形式),通过代数运算解决.解法2借助图形将抽象的问题直观地表达出来,使问题变得更直观、简单,求解更快速、准确.
向量是数形结合的载体,向量的坐标表示把点与数联系了起来,既为我们用代数方法研究几何问题提供了可能,也为我们用几何的观点处理某些代数问题丰富了研究的范围和手段,这正是向量已成为中学数学课程的主角的原因所在.

