基于Memoryless算法的河道水下地形模型简化研究

陆 凤，陈 莉，朱相丞

（1.南京市长江河道管理处，江苏 南京 210011；2.漳州市测绘设计研究院，福建 漳州 363000）

随着水下地形测绘技术的不断发展，特别是多波束测深系统、水声纳系统与激光测深系统的应用，获取海量河道地形数据逐渐成为常态。常见的河道水下地形数据类型包括水声纳扫测数据、河道断面测量数据、等高线与河道深泓线、地理影像图等。河道地形数据量的急剧增加，直接导致所构建的三维模型既精细又庞大，对计算机的存储容量、传输效率、分析处理以及绘制速度等都提出了更高要求。

然而，高分辨率的地形三维模型并非总是必要的。在模型精确度与复杂度之间需要一个折中，即需对模型进行简化，再用简化后的模型代替原始模型。模型简化是指在保持原始模型拓扑结构的前提下，利用适当的算法减少原始模型几何要素数量的过程。模型简化后可减少对硬盘和内存的需求、加速对形状信息的计算，适当缓和海量数据与计算机软硬件资源之间的矛盾。

早在20世纪70年代，就有学者开始讨论网格模型的简化问题。1976年，James Clark最先提出多分辨率模型的概念，而模型简化是以多分辨率模型表示为基础的[1]。20世纪90年代之后，网格模型简化得到了深入研究，其中层次细节（LOD）模型以其普遍性和高效性得到了广泛应用。LOD模型实质上就是按照一定的算法对原始模型进行简化[2]。对网格模型简化算法的分类有很多种，按照简化时间可分为静态和动态算法[3]。目前，静态简化算法主要包括顶点聚类法[4]、区域合并法[5]、重新布点法[6]和几何元素删除法[7]等；动态简化算法包括层次模型生产算法[8]、渐进格网算法[9]、树结构的LOD模型自动生产算法[10]等。一直以来，国内外学者主要研究地形简化技术，而针对河道地形DEM简化技术的研究相对较少。本文借鉴地形简化技术，结合河道地形的自身特征，对河道模型简化算法进行了研究；以河道水声纳扫测数据、断面测量数据以及等高线数据所构建的河道地形DEM为研究对象，基于改进的Memoryless简化算法，将河道地性线加入模型简化约束条件中，实现了河道DEM地形模型在不同简化比率下的简化。

1 模型简化原理与方法

1.1 河道地形DEM构建

Delaunay三角网（D-TIN）是目前地形TIN的主要生成方法。本文以逐点插入法构建D-TIN，以水下声纳扫测数据、等高线和断面数据为数据源，在AutoCAD中利用ObjectARX技术构建河道D-TIN模型。首先对数据进行分析和处理；然后构建点集的外接多边形，并剖分成多个三角形，形成初始的D-TIN；再将点集中未处理的点依次插入已存在的D-TIN中，并用局部优化法则（LOP）对D-TIN进行优化处理，直至所有点都插入完毕；最后删除外接多边形，完成河道地形DEM的构建。

1.2 河道地形地性线提取

水文分析是河道地形DEM分析的一个重要方面[11]。在进行河道地形简化过程中，加入反映河道地形特征的地性线（分水线、汇水线）约束，能使简化效果更加符合河道实际地形。从河道地形DEM中提取分水线的过程主要包括4个步骤[12]：水流方向计算；洼地处理；汇流累积量计算；提取汇流累积量为零的栅格，得到分水线。汇水线的提取也类似，只是对应的DEM采用反地形，即利用一个较大的数值减去原始DEM高程值，使原始DEM中的汇水线在反地形中变成分水线，再利用分水线的提取方法提取。本文利用ArcGIS的Hydrology功能模块提取河道地形DEM的分水线和汇水线。

1.3 河道地形DEM简化

几何删除法是目前应用最为广泛的一种网格模型简化方法[13]。其简化原则为：尽可能保持原始模型的拓扑结构，逐渐删除对模型几何特征影响相对较小的几何要素，并同步删除包含该要素三角面；同时对删除后产生的空洞进行局部三角化以保持拓扑结构，直至满足用户要求。几何删除法主要包括顶点删除法[7]、边折叠法[14]、三角形折叠法[15]等。

1.3.1 网格简化Memoryless算法

Memoryless算法主要基于边折叠法，其核心为：确定新顶点v的位置、边权值以及选择折叠顺序。

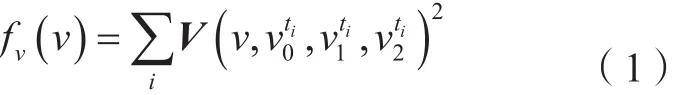
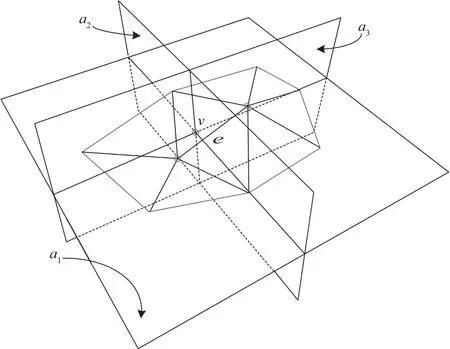
图1 新顶点v由3个平面的交点确定

河道地形DEM是非闭合的曲面，含有较多边界边要素，因此在Memoryless算法中添加保持边界形状的约束条件也是必须的。在边界边的局部区域应尽量保持相邻边界所对应的面积，并计算折叠边界边e之后对应的面积变化量。一般认为，网格模型的边界边是不在同一平面上的，因此选择最小化面积向量模的平方和作为边折叠后边界最优目标函数，计算公式为：

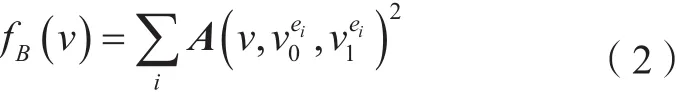
图2中平面a2对应的是边界面积保持约束的顶点集合，平面a3为边界最优对应的顶点集合，平面a1为体积保持约束的顶点集合，因平面a1平行于边界三角形面，故未在图中表示。

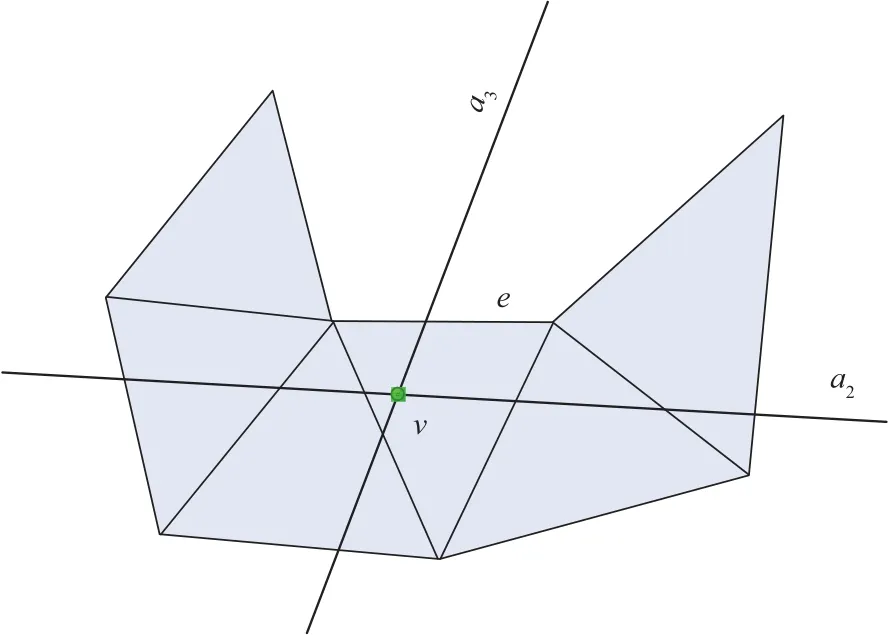
图2 折叠边界边e后的新顶点v

2）边权的确定和选择。在边折叠过程中，定权时应先判定是否为边界边，再对内部边和边界边分别定权，区别处理。依据式（1）、（2），定义网格模型中三角形边的边权值等于体积和边界最优值的加权和，计算公式为：

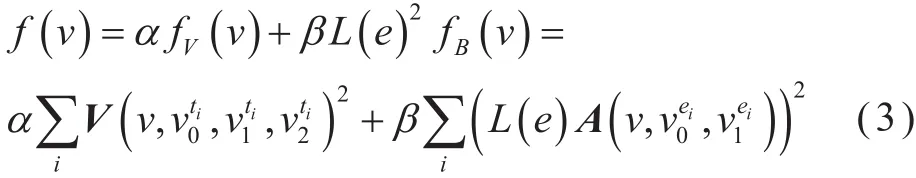
式中，a+β=1。由于fv(v)为体积的平方和，fB(v)为面积的平方和，所以为了保证数量级的一致性，fB(v)需多乘上一个L(e)（边e的长度）。当e为内部边时，a取值为1，β取值为0，即无需添加边界边的面积约束权值；当e为边界边时，a、β取值根据实际需求进行调整，尽量达到对边界边延迟处理的效果。

选择折叠边时，先采用最小堆结构对所有边权进行排序，然后在每次选择时仅需直接从最小堆中取出第一个值对应的边即可。

1.3.2 Memoryless改进算法

虽然Memoryless算法考虑得比较详细，但是对一些特殊情况并没有进行特别处理。本文针对以下两种情况，对该算法进行改进。

1）折叠边的一个顶点是边界点、另一个顶点是内部点（图3）。对这种特殊边的判断方法为：先判断该折叠边是否为边界边，若不是且边的一个顶点是边界点的，即符合该特殊处理条件。

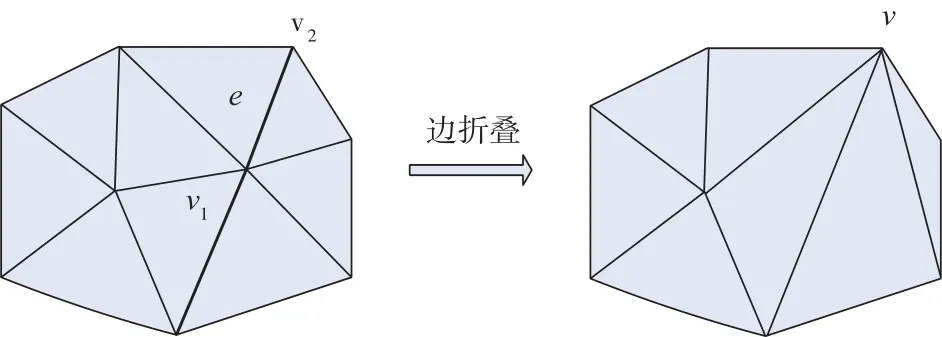
图3 特殊边的折叠操作

2）折叠边相邻的顶点（几近）共面或边界边（几近）共线。这种情况下，函数fv和fB没有唯一解，不能获得新顶点的最佳位置，对于fv和fB较低的边是不利的，因此需添加三角形形状最优化条件来约束。当fv和fB接近于0时，尽量使边折叠操作后的三角形形状趋于等边三角形，避免狭长三角形（狭长三角形会造成阴影的不连续并降低渲染效率）。为了保证三角形的形状质量，选取式（4）作为边长最优的目标函数。

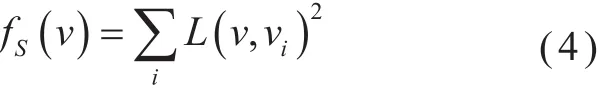
在局部平面或趋于平面的情况下，该平面上新顶点位置的选择对区域体积和面积总和是没有影响的。通过最小化式（4），确保简化后三角形模型的面积与周长的比率是最大的，以提高简化后网格模型中三角形的形状质量。最终定义的边权函数公式为：

式中，a+β+γ=1。通过控制a、β、γ达到不同的简化效果，若要更好地保留模型几何特征，则适当增大a；若要得到平滑均匀的模型，则适当增加γ；特别的，若折叠边e不是边界边，则取β=0。该边权函数能较好地反映边折叠后网格模型的局部几何特征变化，并可通过调节相关系数，达到不同的简化效果。

为了验证Memoryless改进算法的有效性和简化后模型形状保持效果，利用某河道的局部扫测点数据对应的DEM进行实验，如图4所示。为了使对比结果清晰，式（5）中适当增大了γ，内部边的3个边权系数取值为α= 0 .60， β= 0 .00， γ=0.40，边界边的3个边权系数取值为α= 0 .30， β= 0 .30， γ=0.40。

由图4可知，当简化比率高达98%时， Memoryless改进算法获取的简化模型仍能很好地保持河道边界形状，且更好地避免了狭长三角形。

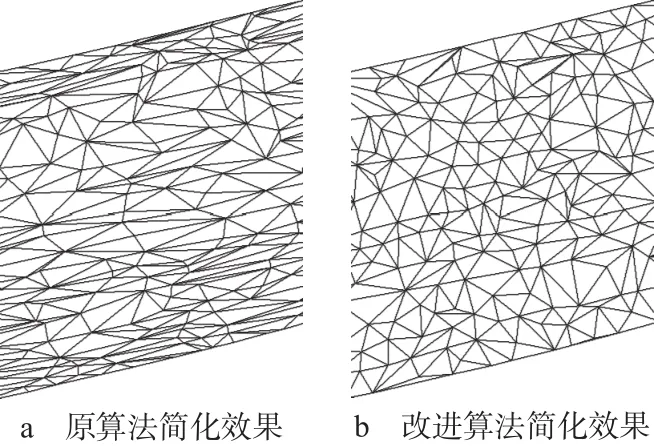
图4 河道地形模型简化至98%效果对比图（局部）

1.3.3 基于河道地性线的简化流程

从河道某点水下地形断面图（图5）可以看出，该处断面最低点C相对于点A、B来说，周边地势较为平缓。在按照改进算法进行简化时，点C及其周边区域所对应的三角形边将比点A、B处的更早被简化，这将导致汇水线及其周边的地形难以保持。同理，分水线附近的地形也可能存在类似情况。因此，需要在模型的简化过程中加入汇水线、分水线约束条件，使地性线周边的三角形边延迟简化，以此达到保持水下地形特征的目的。

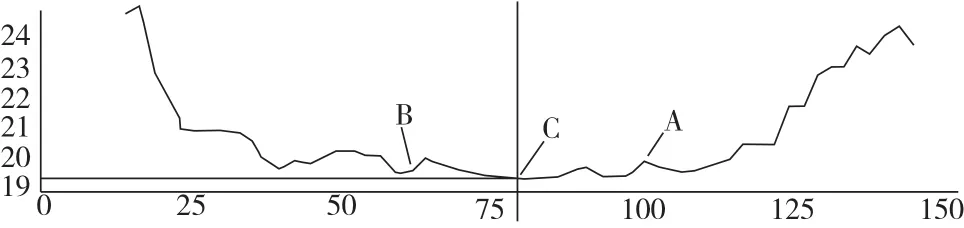
图5 河道某一点处的断面图

河道地形简化后模型的误差度量采用几何误差相似度。首先对简化后的河道网格模型进行一定间距的采样；然后计算简化模型上这些采样点与原始网格模型之间的欧氏距离d1、d2、…、dn；最后统计这些距离中的最大值dmax，并计算对应的中误差值σ，作为河道地形DEM简化后模型的误差判定，其中，简化具体流程如图6所示。

图6 河道地形DEM的简化流程图

图7为截取模型简化至97%的局部放大效果图，在添加河道地性线（图中较粗的虚线）后，可明显看到在地性线左右两侧一定范围内三角形分布较为密集，说明河道地形在地性线周边的细节得到了较好保持。

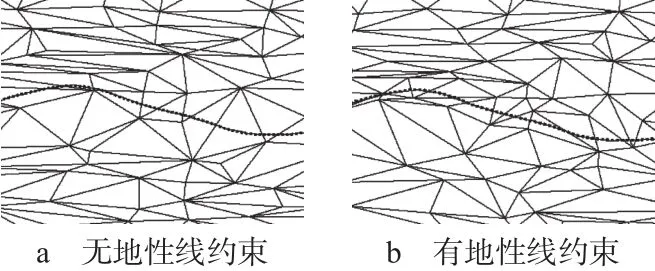
图7 有无地性线约束效果对比图

2 实验结果与分析

实验过程中，需设定或输入简化停止参数，若简化模型对应的值小于停止参数，则模型简化程度已满足需求，停止简化；否则继续简化。根据所需简化后网格模型的精度要求，本文采用简化比率作为停止参数。简化比率为简化后模型折叠的边数与原始模型的总边数的比值，以百分比形式表示。

简化过程中，为了较好地保持河道地形的几何特征，控制边权函数3个系数的取值为：边界边a=0.45，β=0.45， γ=0.10；非边界边 a=0.90， β=0， γ=0.10。根据不同数据来源，对Memoryless改进算法的简化效果进行实验。

1）实验一：研究区域河道长度约为1.5 km，宽度约为85 m；数据来源为等高线和断面点测量数据。简化后部分河道地形模型局部效果如图8所示，对应的相关数据如表1所示，可以看到，在河道中心部分，由于仅分布较少的断面测量数据，当简化比率达到95%时，中心位置地形变化较大；而靠近岸边部分有等高线数据进行加密，河道模型的边界形状和地形特征均保持较好，与现实数据分布情况相符。同时，从表1的数据变化可以发现，简化所用时间、模型误差均随模型简化比率的增加而增大。

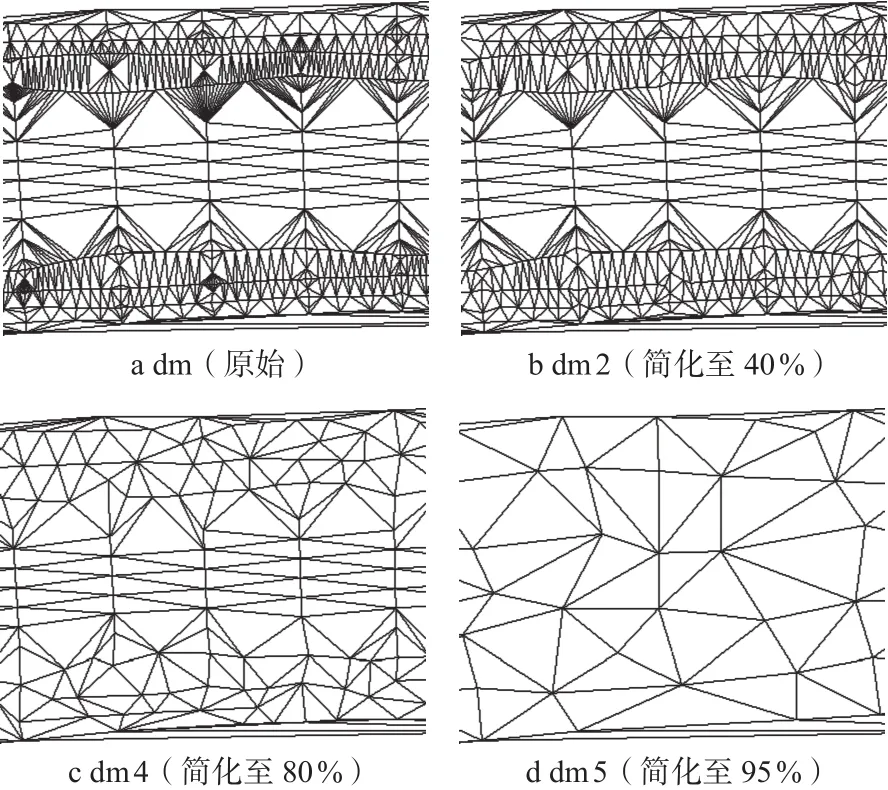
图8 河道地形模型的简化效果（实验一）

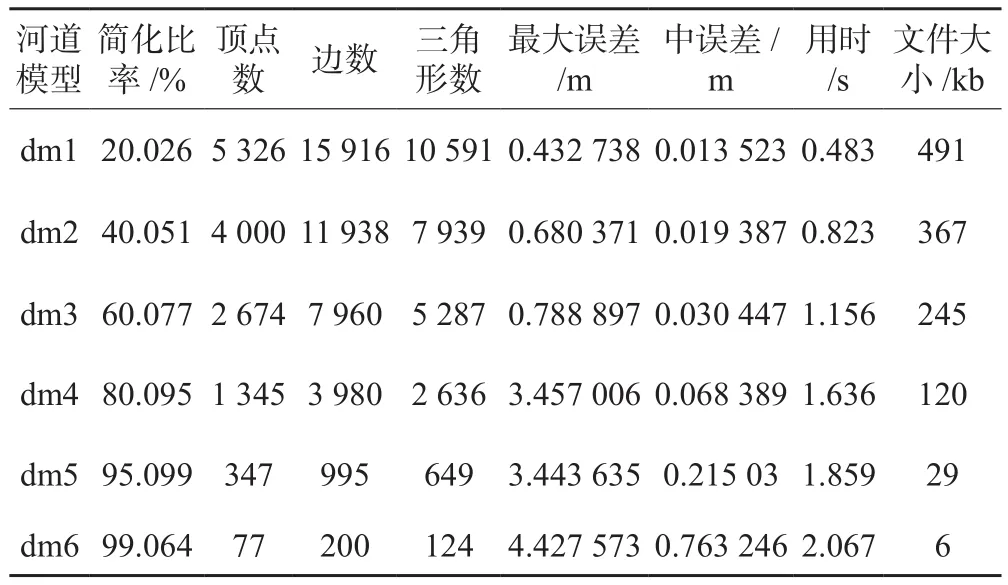
表1 河道地形模型（等高线和断面测量点）简化相关数据表

2）实验二：研究区域河道长度约为2.5 km，宽度约为80 m；数据来源为水下地形扫测数据（约22万个点）。简化后的部分河道地形模型局部效果如图9所示，对应的相关数据如表2所示。

图9 河道地形模型的简化效果（实验二）

结合表2数据可知，当简化比率不高（30%、50%、70%等）时，地形模型的变化不明显，故未在图9中表示；当数据量较大时，经过Memoryless改进算法简化后，河道地形模型不仅能很好地保持模型的边界形状，而且在简化比率较高的情况下，仍能保留河道地形的局部细节特征。表2中的误差数据变化说明简化后的模型误差随着简化比率的增加而增大；模型的中误差均在cm级以内，最大误差均在dm级内，是比较理想的。从文件大小变化可以发现，当可视化仅需较为粗糙的模型时，简化后的模型能使存储量大大降低，对应三角形的数目也随之减少，从而提高显示速度。

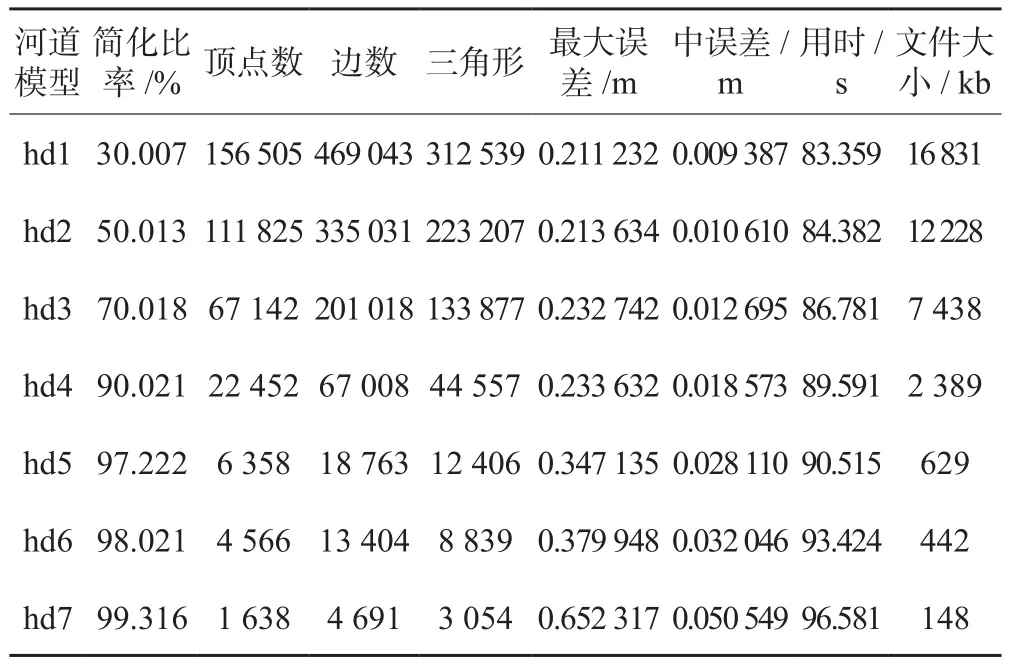
表2 河道地形模型（扫测数据）简化相关数据表

3 结 语

首先在研究Memoryless算法的基础上，结合河道地形DEM实际情况，对算法进行了改进，并将改进后的算法与原始算法的简化成果进行了对比分析；然后在Memoryless改进算法中，增加了河道地性线约束，使得河道地形在地性线周围的细节能够得到较好保持；最后采用两种不同来源的数据对基于地性线的Memoryless改进算法的简化效果进行了实验。结果表明，该算法简化后地形模型效果良好，误差在可接受的范围内，同时也较好地保持了河道地形的几何特征和细节信息。但本文研究的Memoryless算法属于静态简化算法，其简化后生成的模型在不同分辨率之间的切换变化不连续，将产生明显的“跳跃”现象。为了解决这一问题，需对动态简化算法展开进一步研究。