基于罗德里格矩阵的三维坐标转换方法研究

陈林宇

（1.广东省国土资源测绘院，广东 广州 510000）

工程测量中经常需要将GPS处理结果从WGS84坐标系转换到施工建立的独立坐标系；同时为了实现各国家大地坐标参考框架中成果的统一，也经常需要进行三维坐标转换。通常不同坐标系进行坐标转换时，只需3个公共点即可求得唯一转换参数；而在实际应用中，为了提高精度以及检核验算，往往进行多于3个公共点的坐标转换，因此存在多余的观测条件，需进行平差以求解最优转换参数。最常用的三维坐标转换模型为七参数模型，但其参数的初值求解和方程线性化较复杂，不利于编程实现。陈义[1]等以9个方向余弦为参数，采用附有条件的间接平差公式得到了一种三维转换的严密解法。张卡[2]、潘国荣[3]等介绍了基于罗德里格矩阵的三维坐标转换方法，但由于其未对参数进行线性化，也未以坐标差值的平方和最小为准则，所以与传统七参数模型严格线性化后的严密解法有微小差别。姚吉利[4-5]等提出了利用罗德里格矩阵进行三维坐标转换的严密解法。在研究三维坐标转换方法的基础上，本文采用罗德里格矩阵进行三维坐标转换，总结了仅利用3个公共点求解未知参数初值的简便方法，并详细推导了基于罗德里格矩阵的间接平差模型，提出了多个公共点坐标转换的最小二乘严密解法。

1 基于罗德里格矩阵的三维坐标转换模型

根据坐标转换原理，将一个坐标系的点位坐标（X, Y, Z）转换成另一个坐标系坐标（X′, Y′, Z′）的数学模型为：

式中，△X、△Y、△Z为3个平移参数；λ为尺度变化参数；εX、εY、εZ为3个旋转角；R为坐标转换旋转矩阵，R＝R1(εX)R2(εY)R3(εZ)。同时，R 也可理解为由 3 个独立参数组成的正交矩阵，通过反对称矩阵S构建罗德里格矩阵来表达[6]，即R＝（I+S）（I-S）-1，反对称

2 转换参数初值的解算

在平差前，需对非线性方程进行泰勒级数展开线性化，只保留常数项和一阶项。为了提高线性化的精度，需求解转换参数的初值。根据已有的任意3个公共点，求解转换参数的初值△X0、 △Y0、 △Z0、 λ0、 a0、 b0、 c0。

（Xi, Yi, Zi）和（Xj, Yj, Zj）两个公共点根据式（1）相减得到[7]：

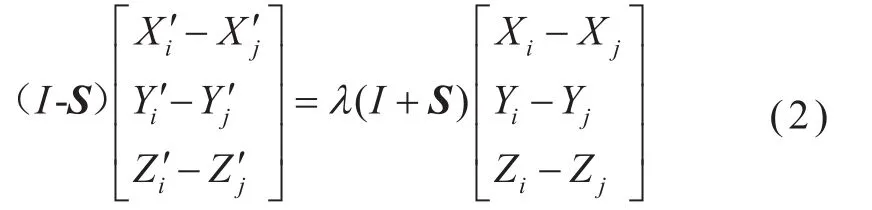
对式（2）进一步转换，得到：

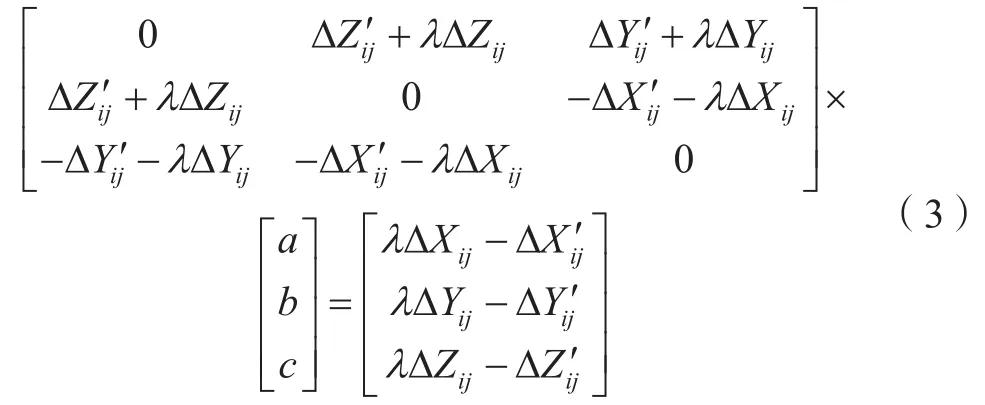
对3个公共点两两组合，根据式（3）组成3个独立方程，联合解算得到参数a、b、c；再根据式（1）得到平移参数。因此，初值计算仅需3个公共点进行简单的方程解算，而且甚至无需编程实现即可求解基于罗德里格矩阵的坐标转换七参数初值，为后续的最小二乘平差求解提供必要条件。

3 基于罗德里格矩阵的三维坐标转换平差

当两个坐标系存在多于3个公共点，即存在多余观测条件时，根据最小二乘原理平差[8]解算坐标转换的 7 个参数：△X、 △Y、 △Z、 λ、 a、 b、 c。

1）根据已有的3个公共点，求解参数初值，并计算R0。

2）对基于罗德里格矩阵的三维坐标转换方程进行泰勒级数展开线性化，只保留常数项和一阶项，得到的平差方程为：

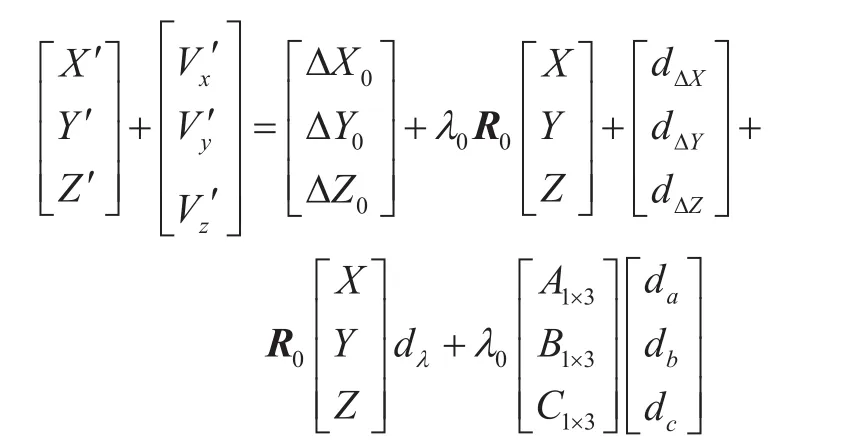
式中，A1×3、B1×3、C1×3分别为：

3）进一步转化得到间接平差的误差方程，代入所有公共点，按照间接平差公式求解所有参数的最小二乘严密平差解：

求得坐标转换参数后，即可根据式（1）进行其他 非公共点的坐标转换。

4 算例分析

本文采用C#语言编制基于罗德里格矩阵的三维坐标转换程序，先利用3个公共点计算初值；再利用最小二乘原理，建立间接平差模型，并代入初值进行方程解算；最终求得坐标转换七参数，进而实现坐标转换。对某一施工项目的P01～P09九个公共点进行坐标转换，公共点在WGS84坐标系和施工坐标系下的坐标如表1所示，将WGS84坐标向施工坐标转换后的坐标减去施工坐标系下的坐标得到表1中的差值。同时，采用七参数严密解法对上述点进行坐标转换，得到的转换后坐标与本文方法得到的坐标一致，验证了本文方法的正确性。

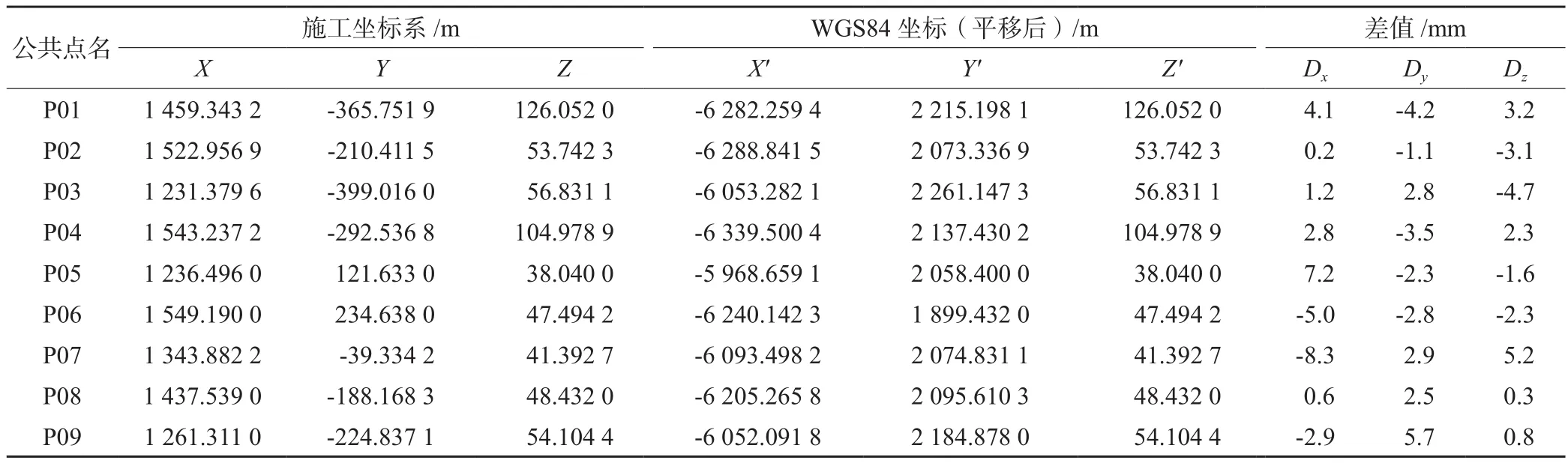
表1 公共点在两套坐标系下的坐标

5 结 语

本文采用罗德里格矩阵进行三维坐标转换，总结了利用3个公共点求解未知参数初值的方法，并推导了利用间接平差模型进行多个公共点坐标转换的最小二乘严密公式。本文编制了基于罗德里格矩阵的三维坐标转换程序，并通过9个点坐标拟合的实例进行了验证，其坐标拟合结果与七参数严密解法的结果一致。本文提出的方法简单可行，易于编程实现，为三维坐标转换提供了一个好的途径，值得推广应用。