测金属线膨胀系数的2种方法

刘肖一,王文彦,平 澄,b

(北京师范大学 a.物理学系;b.物理实验教学中心，北京 100875)

线膨胀系数是金属的重要物理性质,金属由于受热造成的长度改变量与原长度的比值在10-4～10-5量级，为了测量线膨胀系数需要测量微小位移. 常见的金属线膨胀系数的测量方法主要有光杠杆法[1]、交流电桥法[2]和千分表直接读数法[3]. 光杠杆法在操作上较为复杂，千分表直接读数法的误差较大. 光学方法-迈克耳孙干涉法[4]，其特点是精度极高，常被用于测量微小位移；电学方法-RLC谐振电路法，其特点是通过测量电路的谐振频率，间接得到电路中平板电容极板间距的微小变化. 基于上述想法，分别搭建相关的实验装置，实现对线膨胀系数的测量.

1 光学方法测量金属线膨胀系数

1.1 实验原理

迈克耳孙干涉仪的光路图如图1所示. 当平面镜M2关于分束镜BS成的像M2′与平面镜M1平行时，在光屏上可以观察到内疏外密的同心圆干涉条纹.每当M2′与M1距离改变λ/2(λ为所用激光波长)时可以看到1个条纹的陷入或涌出.

将平面镜M1与金属棒相连，金属棒受热膨胀会引起平面镜的平行移动，从而改变两镜之间的距离. 记录下初始时温度t0，条纹改变数为n时的温度t，则平面镜之间距离改变量为

(1)

即金属棒在温度升高Δt=t-t0时的长度改变量. 根据线膨胀系数E的定义有

Δl=lEΔt,

(2)

得出

(3)

其中l为金属棒的原长.以nλ/2为纵坐标，lΔt为横坐标作图，拟合直线的斜率即为线膨胀系数E.

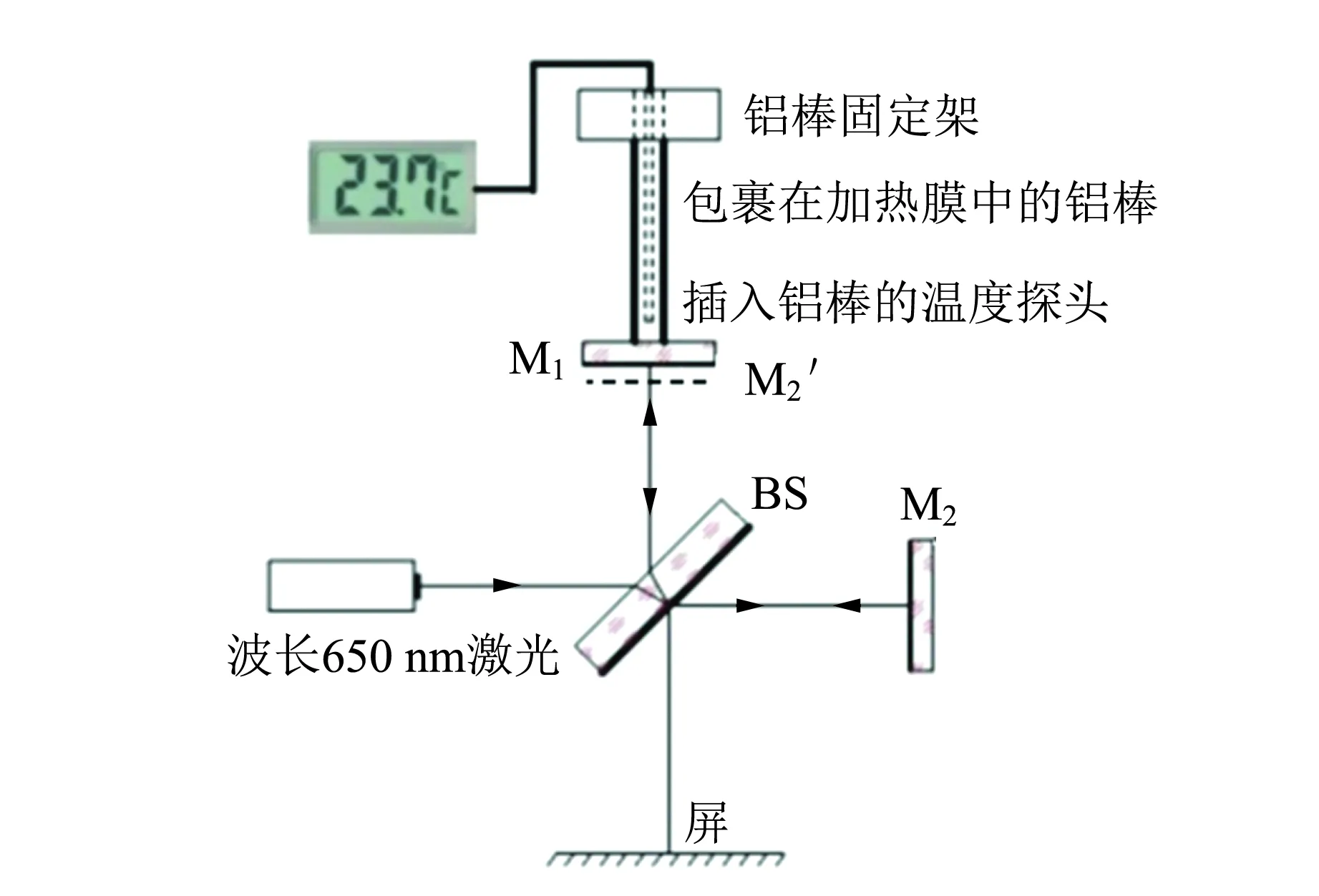
图1 迈克耳孙干涉仪光路图

实验用半导体激光器波长λ=650 nm，包裹在加热膜中的金属棒26.0 ℃时长l=12.00 cm，在光学平台上搭好迈克耳孙干涉仪，如图1所示，调出等倾干涉条纹，记录此时温度T0后，对金属棒进行加热，每有10个条纹变化时记录1次相应的温度t,记录多组数据.

1.2 数据分析与结论

实验测定的物理量及相关计算如表1所示. 对表1中nλ/2-lΔt进行拟合，得到金属杆的膨胀系数为E=2.86×10-5℃.

表1 干涉法温度变化对应的条纹数目变化结果

2 电学方法测量金属线膨胀系数

利用RLC谐振电路对金属棒膨胀系数进行测量，装置如图2所示，电路中的电容用2块平行铝板制成，电容极板A固定，另一极板B与待测金属棒相连，金属棒受热膨胀后将改变电容极板的间距，使得电路中的电容值发生变化，导致电路的谐振频率发生改变，在示波器上用XY模式对电路中电阻上电压和电流的相位差进行监测，当电路发生谐振时，相位差为0.

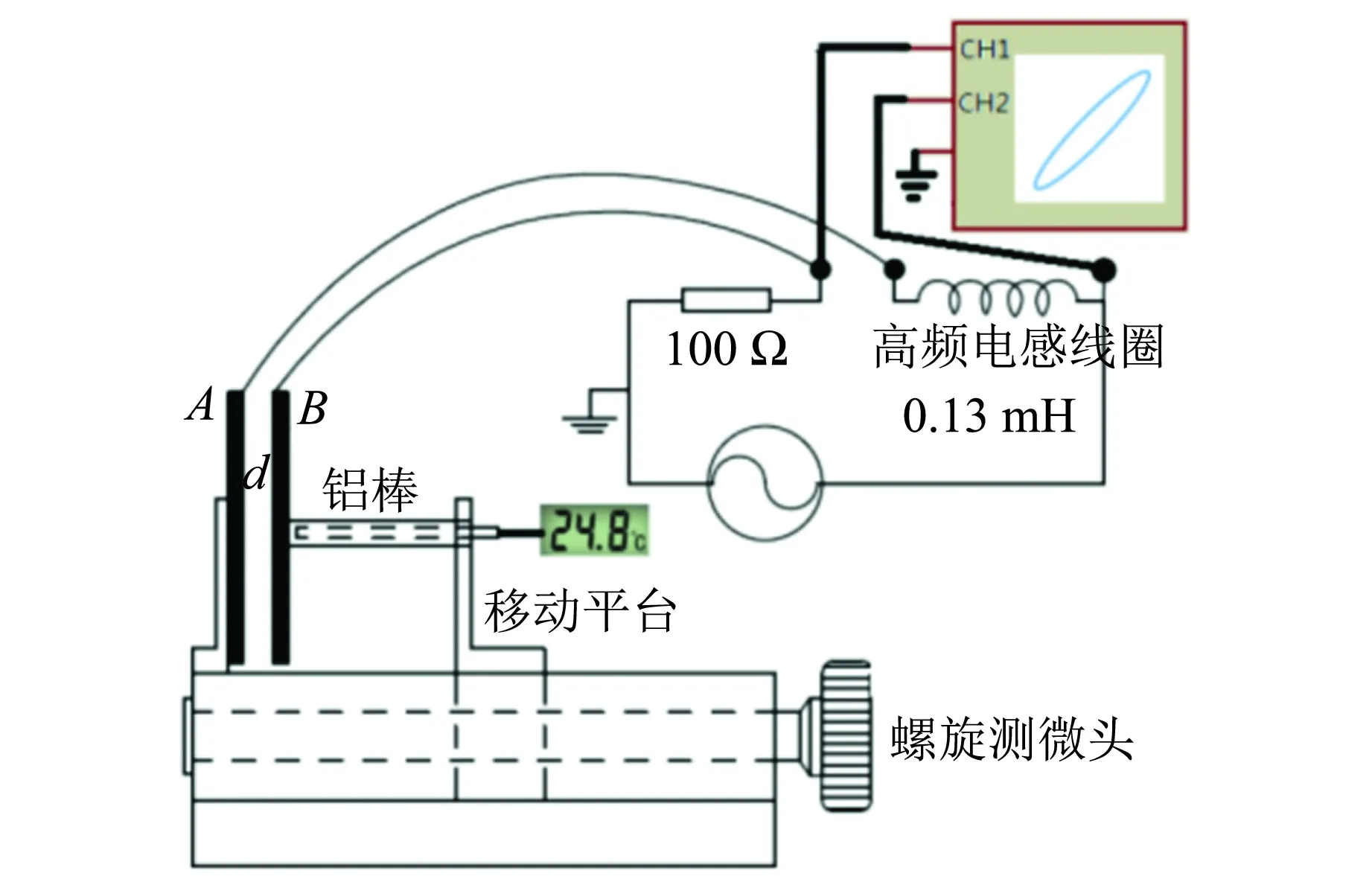
图2 谐振电路及装置图

谐振法可以用2种不同的操作方法间接地得到金属棒的伸长，并计算出金属的线膨胀系数.

实验电路的相关参量：平板电容器尺寸为260 mm×160 mm;金属棒与干涉法用的是同一根,l=12.00 cm，高频电感线圈L=0.13 mH，电阻R=100 Ω.

2.1 方法一:谐振频率补偿法

2.1.1 实验原理

如图2所示，将平板电容与高频电感线圈和电阻串联置于正弦交流电路中，发生谐振时的交流电的频率满足

(4)

其中,L为电感器的电感值，C为电容器的电容值.

调整平行板电容器的极板的初始间距为d0，金属棒受热膨胀时，两极板距离减小，满足

d′=d0-Δl,

(5)

由平行板电容器公式

(6)

d减小时电容增大，由式(4)可知，谐振频率减小. 由以上各式可推出

(7)

从而有

(8)

由式(4)，(5)，(8)式得

(9)

由式(9)可以计算出一系列的Δl，以Δl为纵轴，lΔt为横轴，做线性拟合. 由式(2)可知，直线的斜率即为线膨胀系数E.

2.1.2 实验过程

如图3所示，将平行板电容器的初始距离调整为d0=1.5 mm，加热膜接直流电源对金属棒进行加热，调节信号发生器所输出的正弦波的频率，使电路在不同温度下分别达到谐振状态，记录多组温度及其所对应的谐振频率的值。

图3 装置连接实物图

2.1.3 数据测量与分析

实验测定的各物理量相关计算如表2所示，对Δl-lΔt进行线性拟合，金属杆的膨胀系数为E=2.85×10-5℃-1.

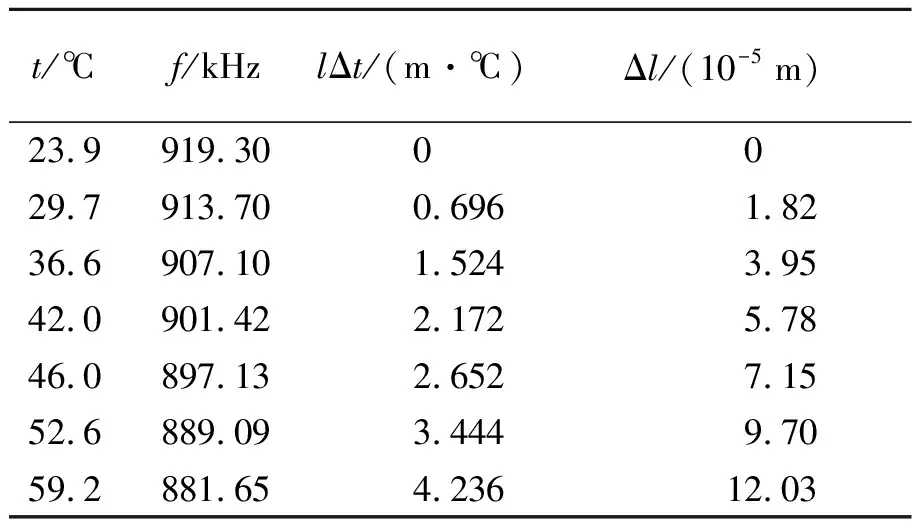
表2 谐振频率补偿法温度变化时各物理量的测量结果

注：d0=1.50×10-3m

2.2 方法二：电容极板间距补偿法

2.2.1 实验原理

使谐振频率不变，改变平板电容器极板间的距离，使得金属棒在不同温度下，电路始终处于谐振状态，测量每次改变的电容极板距离l，该距离就是金属棒受热膨胀后的伸长量。

2.2.2 实验过程

调整平板电容器极板平行，调整极板间距使电路谐振频率在800 kHz左右，加热膜接直流电源对金属棒进行加热，转动螺旋测微头，通过移动平台移动极板B，使电路的谐振频率在不同温度下保持不变，通过螺旋测微头读出不同温度t对应极板B移动的距离，直接利用式(2)线性拟合，斜率即为金属棒的膨胀系数。

2.2.3 数据测量与分析

实验测定的各物理量及相关计算， 如表3所示，对Δl-lΔt进行线性拟合，得到金属杆的膨胀系数为E=2.83×10-5℃-1.

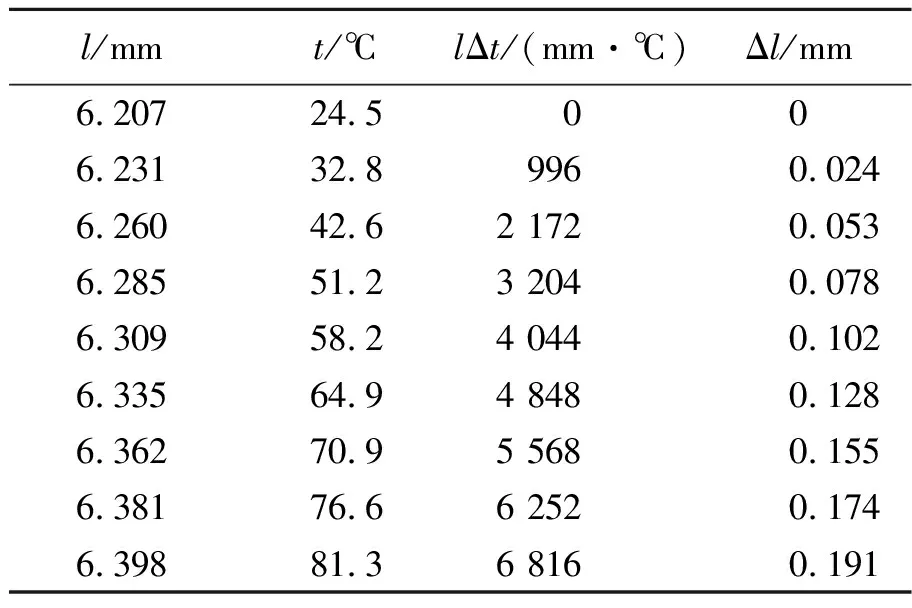
表3 电容极板间距补偿法温度变化时各物理量的测量结果

3 光学方法与电学方法的对比

3种方法测出的线膨胀系数之差在10-7℃-1量级，测量结果非常接近.

光学法的优点是精度高，可以分辨可见光波长量级的长度改变. 但是如果待测金属棒密度不均匀，加热后会导致图1中M1与M2′的平行度发生微小改变，使得看到的干涉条纹中心向视场外移动，最终会导致无法对条纹计数。

电学法的精度相比光学法较低，主要是因为装置的螺旋测微头只可以分辨10-5m的长度改变. 但其优势是实验装置稳定，室内温度、湿度、外界轻微干扰等因素对实验影响都可以忽略[5]. 另外，电容器自身的温度升高会使得品质因数下降，从而导致测得谐振频率的轻微下降[6]，从而引入一定误差.

4 结束语

材料的线膨胀系数是材料的热学物理性质之一，是表征材料性质的重要特征量，正确掌握固体线膨胀系数的规律性，对于基础科学研究、技术创新、工程技术的设计与应用等都具有重要意义. 本文对用光学和电学方法测金属线胀系数的实验进行了详细叙述，可为在校大学生提供利用光的干涉或谐振电路解决实际问题的方法，加深对相关物理知识的理解，这些方法在工程实践中也有很有意义[7].

致谢：实验过程中获得北京师范大学物理实验教学中心王引书老师和白在桥老师的帮助，实验所用高频电感由北京师范大学2015级莫裕宇、刀流云同学手工绕制,在此表示感谢.