稳态核磁共振实验中弛豫时间T2的测量方法
杜晓波,付成伟,纪 媛,吕佳明,杨博闻,夏书涵, 孙 昕,梁桁楠,崔 航,龙北玉
(吉林大学 物理学院,吉林 长春 130012)
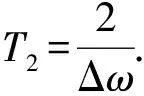
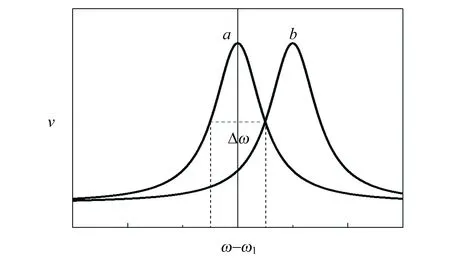
图1 氟原子核的核磁共振吸收信号
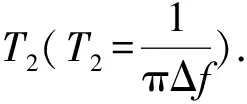
由于ω=γB,图1的横轴也代表磁场. 本文研究另一种测量T2的方法,即在静态吸收曲线图像基础上(无需调整射频磁场的频率),通过Origin软件测量吸收曲线半高全宽对应的磁场的变化ΔB,再由ΔB计算出T2.
1 实验装置
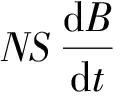
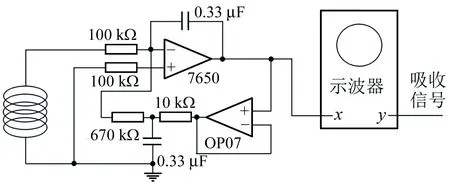
图2 50 Hz交变磁场获取原理图
积分器由低漂移的7650集成运放和电阻、电容组成. 将输出信号中的直流成分(即漂移电势)取出反馈到7650集成运放的负输入端,进一步抑制漂移. 经测试,输入端短路后漂移信号可维持在50 mV左右,且非常稳定,不会使积分器饱和,从而不会影响到50 Hz交变磁场的测量. 通过测量,积分器输入和输出信号的相位非常接近90°,积分器性能达到设计要求.
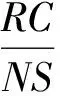
2 实验方法
2.1 吸收信号获取
将积分器输出信号输入到示波器(日本横河DLM200)1通道,吸收信号输入到示波器2通道,调整示波器到x-y扫描方式,即得到图3所示的共振吸收信号. 在50 Hz扫描电压不变的情况下,调整射频磁场的频率,吸收峰左右移动,但是峰宽基本不变,可见x轴与磁场成线性关系. 2个吸收峰不在同一磁场下出现,是由于磁场的变化有一定的速度,吸收信号的出现要滞后于磁场的变化,尽管氟样品的弛豫时间T2较小. 曲线不闭合是由于50 Hz市电信号的干扰.

(a)24.163 MHz

(b)24.227 MHz

(c)24.441 MHz图3 x-y扫描模式下不同射频场频率的吸收信号
2.2 吸收信号处理
理论上,吸收曲线满足
(1)
式中,B1,T1,T2,ω,ω1,M0分别为射频磁场的幅度、纵向弛豫时间、横向弛豫时间、总磁场B对应的角频率(ω=γB)、射频磁场的角频率和样品的磁化强度. 一般情况下射频场B1很弱,分母最后一项可忽略,则
(2)
可见吸收曲线符合洛伦兹线型.
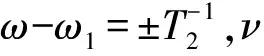
(3)
由Origin软件处理示波器存储的csv格式数据,如图4所示.

图4 Origin软件对吸收曲线拟合处理
图4的横轴为积分器输出的电压. 恒磁场B0不会在线圈中感应出电压,因此积分器输出的电压对应于50 Hz交变磁场. 在根据实验测定的积分器系数0.241 T/V,可得到图4中50 Hz交变磁场的峰峰值为0.011 4 T.
从图4能够看出共振信号除了吸收峰外,还含有很强的50 Hz的市电干扰信号,使背底不是1条水平直线. 同时干扰信号使得吸收峰变形,影响到半高全宽的测量. 不同的仪器干扰信号不同,规律性较差. 为更准确得到吸收峰从而测量出半高全宽,应从曲线中分离出背底信号. 因此除了要对吸收峰进行拟合外,还要对干扰背底信号进行拟合.
以洛伦兹峰函数
(4)
对吸收信号进行拟合. 用多项式
y=A0+Bx+Cx2+Dx3
(5)
拟合背底. 图4中黄色曲线为拟合的吸收峰和背底的叠加. 由Origin软件给出的上部的吸收峰和下部的吸收峰的半高全宽分别为0.001 3 V和0.0013 3 V,相差小于3%. 对应的磁场分别为0.000 313 T和0.000 321 T. 由(3)式计算出相应的弛豫时间T2为23.8 μs和23.2 μs.
3 结束语
在核磁共振实验中,采用线圈和电子积分器获得了与50 Hz扫描磁场成正比的信号. 采用核磁共振方法对积分器进行标定,可以由积分器输出电压直接得到50 Hz扫描磁场的峰峰值. 以此信号作为x轴,得到了以磁场为变量的氟原子核的静态的共振吸收信号. 利用Origin软件强大的数据处理能力,对信号进行拟合处理计算,得到了氟原子核的横向弛豫时间T2. 与传统的测量T2实验方法比较,这种测量比较简单,测量结果更为精确.

