耦合图像间的数据融合算法

任晓旭，吕良福，崔广泰

(1.天津大学 数学学院，天津 300072； 2.河海大学 理学院，南京 211100)(*通信作者电子邮箱liangfulv@tju.edu.cn)

0 引言

随着电子和成像技术的发展，针对实际中产生的大量医学[1]、信息遥感等数字图像，人们很难找到需要的精确数据，而这种局面也促使人们希望可以通过计算机技术自动分析海量图像，通过算法快速有效地选择特征的信息，提高效率。一般情况下，多通道图像等数据本身就具有天然的张量结构，另外由于张量结构具有良好的表达能力和计算特性，所以研究图像的张量分析是非常有意义的工作，其中张量分解能够保持原图像数据结构特性。针对高光谱图像，张量分解可以充分利用图像之间的空间和谱间冗余，快速而高质量地对高光谱图像进行压缩和提取相关的特征信息[2]。文献[2]基于高光谱图像提出非负张量标准分解(Canonical Polyadic decomposition, CP)算法，并用于解决盲源信号分离问题。Shashua等[3]将CP分解用于图像压缩和分类，Bauckhage[4]将判别分析(discriminant analysis)引入到高阶数据如彩色图像中进行分类。而对于类似高光谱与多光谱图像的多源异构数据，其数据之间的隐含模型通过它们的变量子集耦合，这里的耦合是指这些变量子集之间的关联关系，即图像经过张量分解后的因子矩阵之间存在耦合关系[5]。本文希望利用图像之间的这种耦合关系，通过张量分解算法从其中一个数据集的信息提高对其他数据集估计精度和完善对相关的潜变量的解释。

在实际的应用中，来自不同数据源的数据分析需要处理异构数据集，即矩阵或高阶张量[6]。对于一些耦合矩阵和张量的数据分析，文献[7] 中提出了相应的耦合矩阵和张量分解优化(Coupled Matrix and Tensor Factorization-OPTimization, CMTF-OPT) 方法。而相应的实验结果表明，在一定的噪声干扰下，耦合矩阵和张量分解(Coupled Matrix and Tensor Factorization, CMTF)方法比CP算法在数据恢复方面具有更好的性能。类似地，文献[5]中也研究了高阶的耦合张量分解问题，并通过实验结果表明,该模型在耦合张量分解方面有更好的性能。文献[5]中针对不同数据之间的耦合关系及耦合下的数据分解算法进行了研究，该算法表明基于耦合数据的分解算法比交替最小二乘(Alternating Least Squares, ALS)法具有更好的收敛性，且算法计算的花费时间更少。因此，利用图像本身之间的耦合关系进行图像分解是非常有必要的措施和工作。

本文提出了基于CMTF-OPT算法[7]的耦合图像分解优化(Coupled Image Factorization-OPTimization, CIF-OPT)算法，针对文献[8]中的改进CMTF(Advanced CMTF, ACMTF)算法，将该算法应用到图像中形成改进耦合图像分解(Advanced Coupled Image Factorization, ACIF)算法。针对CIF-OPT和ACIF两种耦合图像分解算法，通过对比实验得出，两种算法对耦合图像的分解均具有可行性，但是在低噪声水平下，CIF-OPT比ACIF算法具有更好的融合效果。故基于CIF-OPT算法提出针对缺失图像的数据恢复方法，即利用耦合图像分解算法恢复或者近似还原缺失图像的数据。

1 背景知识

1.1 符号说明

为了更好地研究耦合图像之间的数据融合，本文首先引入以下的一些符号与定义。本文用希腊字母表示张量，如：N阶张量Φ∈RI1×I2×…×IN。对于大小为I×J的矩阵A,张量的矩阵化是指张量按模展开为矩阵，其主要的目的是对张量进行降维，如张量Φ∈RI1×I2×…×IN以第n模展开记作X(n)。矩阵向量化是将矩阵按列展开形成一个长度为IJ的列向量,即:

给定两个矩阵A∈RI×K和B∈RJ×K，其Khatri-Rao积记作A⊙B，计算结果为大小IJ×K的矩阵，即:

其中：“⊗”表示克罗内克积。

给定两个张量Ψ，Θ∈RI1×I2×…×IN，张量的内积记作内部元素乘积的和，即:

对于一个张量，用“×n”表示张量的模式积，即对于一个张量Φ∈RI1×I2×…×IN和一个矩阵Y∈RJ×In的n-mode乘积Φ×nY∈RI1×…×In-1×J×In+1×…×IN，其中元素定义为:

给定两个张量Ψ,Θ∈RI1×I2×…×IN,其Hadamard积记作Ψ*Θ，计算结果为大小为I×J的矩阵，即：

1.2 张量分解

在实际的应用中，一般张量分解模型分为两类：标准分解(Canonical Decomposition，CP)模型和Tucker分解模型。其中：CP分解模型最初是由Carroll等[9]和Harshman[10]分别单独提出；Tucker模型是由Tucker[11]在1966年提出的,而CP分解模型是Tucker分解模型的一种特殊情况。当时模型的提出都是为了提取心理学测试中得到的数据特征。对于一般的矩阵模型，可以借助矩阵的奇异值分解、非负矩阵分解等来提取矩阵数据的潜在特征信息，例如多光谱数据融合、盲源信号分离等问题。同矩阵的低秩逼近的思想类似，人们也想借助张量的分解模型来提取张量模型数据中潜在的内部结构信息。

对于一个一般的N阶张量Φ∈RI1×I2×…×IN,CP分解表示为：

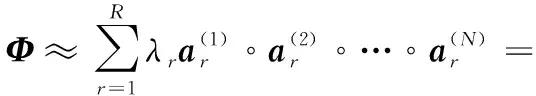
特别地，对于三阶张量Φ∈RI×J×K的CP分解表示为：

其中：对于r=1,2,…,R，ar∈RI,br∈RJ,cr∈RK；因子矩阵A、B、C的列被标准化为1；λr为权重。如果将权重分配到因子矩阵中，则CP分解也可表示为：

Φ≈(A′,B′,C′)

现在定义Ωr为R个由λr构成的R×R×R阶的对角张量，故上式可以转化为：

Φ≈(A,B,C)·Ωr

2 耦合数据融合

2.1 耦合数据融合的相关工作

本文考虑来自异构数据源的耦合数据间的融合。Singh等[12]提出的集体矩阵分解(Collection Matrix Factorization, CMF)利用数据集之间的相关性的不同，同时对耦合矩阵进行因式分解。

考虑两个矩阵X∈RI×M,Y∈RI×L，一般的CMF分解模型通过最小化目标函数(1)来建立：

f(U,V,W)=‖X-UVT‖2+‖Y-UWT‖2

(1)

其中:矩阵U∈RI×R；V∈RM×R；W∈RL×R是因子矩阵；R是因子的数量。

在实际生活中，由于存在大量的高阶数据，故下面讨论耦合张量与矩阵之间的数据融合。

对于张量Ξ∈RI×J×K,矩阵Y∈RI×M，本文假设耦合只发生在第一个因子矩阵中。实际上，一般的耦合矩阵和张量分解模型通过改变目标函数(2)来建立：

(2)

其中：矩阵A∈RI×R,B∈RJ×R,C∈RK×R是张量Ξ经过CP分解后的因子矩阵。

将上述建立的模型称为耦合矩阵和张量分解(CMTF)问题，在文献[7]中提出了基于耦合矩阵和张量分解的交替最小二乘(CMTF-Alternating Least Squares, CMTF-ALS)算法。基于ALS的算法实现简单、计算量小且有效，然而，在缺少数据的情况下，基于ALS的算法收敛性很差[13]。另一方面，用一次优化的算法同时求解所有CP因子矩阵更具有鲁棒性，而且更容易推广到缺失数据的数据集中[14]。因此，对于高阶的数据集，文献[7]提出了效果更好的CMTF-OPT算法。本文基于此算法提出针对耦合图像的CIF-OPT算法，描述了异构图像数据集的耦合分析，算法类似文献[15]， 但具体步骤基于梯度优化，能够同时求解所有因子矩阵。

目标函数(2)中隐含地假设矩阵和张量因子矩阵A的所有列，也就是ar对于矩阵和张量是共享的。然而，一般来说，耦合数据集中也存在共同的和独立的因子。因此，文献[5]将这样的问题建立了另一种优化函数，即在CMTF中增加共同和独立的成分，对目标函数(2)的修改如下：

(3)

s.t.‖ar‖=‖br‖=‖cr‖=‖vr‖=1；r=1,2,…,R

2.2 耦合图像分解算法

2.2.1 CIF-OPT算法

本文主要针对耦合图像之间的数据融合。一般的，图像以张量和矩阵的形式进行数据存储。本文基于CMTF-OPT算法[5]提出了基于图像数据融合的CIF-OPT算法。考虑矩阵和N阶张量图像在一个模式因子矩阵下耦合，其中张量图像通过CP模型进行分解[16]，矩阵图像通过矩阵分解进行分解。设张量图像Ξ∈RI1×I2×…×IN,矩阵图像Y∈RI1×M，并在第n个因子矩阵耦合，其中n∈{1,2，…,N}，则这两个图像数据集之间的耦合分析的目标函数可表示为：

f(A(1),A(2),…,A(N),V)=

(4)

其中将函数的第一项记作：

f1(A(1),A(2),…,A(N))=

将函数的第二项记作：

本文的主要目标是找到因子矩阵A(i)∈RI1×R和矩阵V∈RM×R使得目标函数(4)最小化。其中，针对上述的优化问题，能够计算其梯度然后使用文献[17]的任意一阶优化算法进行求解。下面，本文将讨论目标函数的梯度。

其中：f1对于A(i)的偏导数已经在文献[18]中进行了相应的推导，具体形式如下。

类似地，矩阵A和V是矩阵Y经过矩阵分解之后得到的因子矩阵。

A(-i)=A(N)⊙…⊙A(i+1)⊙A(i-1)⊙…⊙A(1)

第二部分函数相对于A(i)和V的偏导数如下：

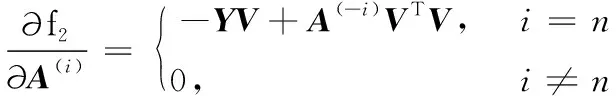
结合上述计算结果，能够计算目标函数f。

相对于因子矩阵A(i)和V的偏导数，如下：

对于一些缺失数据的数据集仍然可以进行耦合分析。CIF-OPT算法的实现可以忽略缺失的数据，只对已知的数据元素进行耦合分析，找出数据满足的张量或者矩阵模型。因此基于上述提出的耦合图像分解算法，将该算法应用于缺失图像中，通过与其耦合的图像恢复出原始的缺失图像数据。

对于所有的in∈{1,2,…,In}和n∈{1,2,…,N}，引入张量Ξ*∈RI1×I2×…×IN来表示张量Ξ中的缺失的数据：

则修改目标函数(4)为：

fΞ*(A(1),A(2),…,A(N),V)=

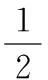
同样地，将函数的第一项记作：

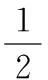
因为修改过后的函数第二项保持不变，则目标函数函数相对于A(i)和V的偏导数如下：

2.2.2 ACIF算法

考虑矩阵图像和3阶张量图像在第一个模式因子矩阵下耦合，其中张量图像通过CP模型进行分解，矩阵图像通过矩阵分解进行分解。设张量图像Ξ∈RI×J×K，矩阵图像Y∈RI×M，则这两个图像数据集之间的耦合分析的目标函数如(3)表示。为了将上述目标函数转化为可微的无约束优化问题，文献[8]将上述优化函数增加了二次惩罚项，对于任意的趋于0的常数ε>0，β≥0和α>0，如式(5)所示：

(5)

与CIF-OPT算法类似,基于文献[8]使用梯度优化方法最小化上述的目标函数，并计算目标函数f的梯度，具体形式是一长度为P=R(I+J+K+M+2) 的向量，是通过对每一个因子矩阵的偏导数进行向量化而得到的。

3 实验和结果分析

3.1 数据生成

本文将两种耦合矩阵和张量分解方法运用到多幅多光谱和全色图像中，原图如图1所示。图像为位于中国北京某地的低空间分辨率的多光谱图像和对应地区的高空间分辨率的全色图像。实验数据来源于机载可见光/红外成像光谱仪(Airborne Visible Infrared Imaging Spectrometer, AVIRIS)拍摄的北京两个地区的数据。AVIRIS数据可提供224个谱段,有20 m的空间分辨率，覆盖光谱范围是0.2～2.4 μm，光谱分辨率为10 nm。选取多光谱图像的数据大小分别为300×300×3和256×256×3像素，全色图像大小为300×300和256×256像素，如图1所示。

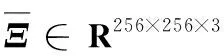
针对CIF-OPT算法，在数据生成方面，本文从多光谱图像和全色图像采样出原始数据，运用交替极小算法对两种图像进行分解，得到初始的因子矩阵，对得到的因子矩阵作张量积和矩阵乘法运算得到无噪声的初始张量和矩阵。其中，张量和矩阵有一耦合的因子矩阵。不失一般性,本文将其设为A。为了更好地研究该算法的性能，本文在不同的噪声水平下对算法进行实验。

例如，本文读取其中一个地区的多光谱和全色图像，经过初始化后生成原始的三阶张量Ξ∈R300×300×3和矩阵Y∈R300×300。然后对张量增加高斯噪声，即:

其中:Ξ1∈R300×300×3为产生的随机高斯噪声张量；η用于控制噪声水平。类似地，对于矩阵Y添加高斯噪声，即:

其中：F∈R300×3为产生的随机高斯噪声矩阵；η用于控制噪声水平。为了研究不同噪声水平下耦合图像分解的效果，在本文的实验中设置了三种不同的噪声水平，即η为0.10、0.25和0.35。作为CIF-OPT算法的终止条件，需满足:

▽f=|fk+1-fk|/fk≤10-8

其中f为目标函数。此外，对于CIF-OPT算法，为了保证算法的可行性，函数值的最大数设置为104，最大迭代次数设置为103。在实验的过程中，算法的终止条件取决于函数值迭代前后的变化。

因文献[8]中提出的改进后耦合数据分解算法基于参数β=0.001，α=1进行数据实验，并将其应用于代谢组学中获得了很好的实验结果。故本文采取相同参数数值进行类似耦合图像的实验，即针对ACIF算法，基于β=0.001，α=1来进行两种耦合图像算法之间的比较。在ACIF算法的数据生成方面，首先从多光谱图像和全色图像读取出原始数据，运用交替极小算法对图像进行分解，得到初始的因子矩阵，对得到的因子矩阵作相应运算得到无噪声的初始张量和矩阵，即Ξ=(λ;A,B,C)和与其耦合的矩阵Y=AEVT，其中λ和对角矩阵E的对角元素σ分别对应秩一张量和矩阵的权重，其中元素个数为R。类似地，对初始张量和矩阵增加噪声来检测算法的鲁棒性。本文旨在寻找融合效果更好、有效且准确的耦合图像分解算法，故对针对两种耦合图像分解算法从算法最优值、迭代次数、误差等方面设计对比实验，多角度地分析了两种算法的有效性。

图1 不同地区的多光谱图像与全色图像Fig. 1 Multispectral and panchromatic images in different regions

3.2 实验结果

本文主要思想是将耦合数据分解算法应用到具体的耦合多光谱图像和全色图像中。针对耦合数据分解算法，生成与地区一和地区二相同维数的随机数据，并应用耦合数据分解中的CMTF-OPT算法对耦合数据进行分解。针对具体的耦合图像，通过CIF-OPT优化算法对耦合多光谱图像和全色图像进行数据融合，即将CMTF-OPT算法的应用范围转化到耦合图像中进行分解，得到的具体结果如表1所示。

表1 基于不同算法不同噪声水平下的图像融合效果Tab. 1 Image fusion effect based on different algorithms with different noise

从耦合数据到耦合图像分解算法的数据变化可以看出，耦合图像算法比耦合数据算法收敛所需的迭代次数更多，收敛所需达到的函数最大数也越大。上述结果是必然的，因为在对耦合图像进行分解融合时需对耦合图像初始化，将图像转为耦合数据进而实现算法，因此收敛需要更多的迭代次数。相应地，通过观察对耦合图像添加噪声的实验可以得出，在噪声水平一定的条件下，本文提出的CIF-OPT算法可以实现耦合图像的分解，且算法的结果与耦合数据分解算法的结果接近，同时在一定的噪声水平下的分解效果要优于CMTF-OPT算法。而CIF-OPT算法对不同图像的融合效果一致，因此具有一定的鲁棒性，而且融合效果并不会因为图像阶数和数据元素的改变而发生变化，算法的迭代次数也并不随阶数的增加而剧增。通过比较，发现CIF-OPT算法效果好，故算法是可行的。

针对耦合数据分解的另一种ACTMF(Advanced Coupled Matrix and Tensor Factorization)算法[8]针对地区一进行了相同的噪声水平实验，并与CMTF-OPT算法进行了比较，结果如图2所示。

图2 不同噪声水平下耦合数据分解算法的目标函数值比较Fig. 2 Object function values comparison of coupled data decomposition algorithms with different noise level

从图2可以看出，改进后的耦合数据分解算法即ACMTF算法在不同的噪声水平下均优于CMTF-OPT算法。故本文基于相同的参数和噪声条件，针对耦合图像的另一种ACIF算法进行了相同的噪声水平实验，并对两种耦合图像算法之间的目标函数值、迭代次数、误差等参数结果进行了比较，在不同噪声水平下的融合效果如图3所示。

图3 不同噪声水平下耦合图像分解算法的目标函数值比较Fig. 3 Object function values comparison of coupled image decomposition algorithms with different noise level

实验结果表明，在添加的噪声小于0.2时，CIF-OPT算法比ACIF算法更加有效。这与两种算法在耦合数据中对数据的融合效果不同，且随着噪声水平的增加，两种算法在融合效果方面的表现几乎无异，这表明改进后的图像分解算法并不具有比CIF-OPT算法更好的优势。接着针对算法收敛所需的迭代次数进行了对比，结果如图4所示。可以看出，ACIF算法收敛所需迭代的次数在大多数情况下比CIF-OPT算法的迭代次数多，在算法运行时，它达到收敛条件至算法终止花费的运行的时间也更长。为了综合考虑各方面因素，本文计算4种算法的融合误差来全面地比较算法对数据分解的准确性，具体结果详见图5。

图4 不同噪声水平下耦合图像分解算法的迭代次数比较Fig. 4 Iteration times comparison of coupled image decomposition algorithm with different noise level

从图5可以看出，在一定程度上，虽然耦合图像的分解效果要比耦合数据的效果好，但是耦合数据分解算法的误差具有一定的稳定性，且误差值低于耦合图像分解算法。对于耦合图像分解的两种算法来说，在噪声水平低于0.25时，两种算法的误差值不稳定，图5误差值量级小，因此随着噪声水平的增加， CIF-OPT算法的误差与ACIF算法的误差值十分接近。故对于耦合图像分解算法，在低噪声水平下CIF-OPT算法表现出更出色的融合效果，且误差值和算法收敛所需迭代次数更少。上述算法主要基于地区一进行结果比较，下面基于CIF-OPT算法，针对两个不同的地区从算法的迭代次数方面、目标函数值的差距等方面进行对比，结果如图6～7所示。可以看出算法收敛的迭代次数与图像大小并没有明显的线性关系。因图7量级很小，故两个地区的目标函数值非常接近，即CIF-OPT算法的函数最优值并不会因为图像大小和像素的不同而产生显著的变化。

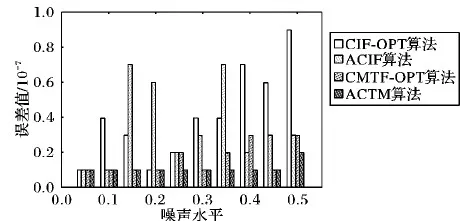
图5 不同噪声水平下4种耦合分解算法的误差值比较Fig. 5 Error values comparison of 4 coupled decomposition algorithms with different noise level

图6 不同地区下耦合分解算法的迭代次数比较Fig. 6 Iteration times comparison of coupled image decomposition algorithms in different regions

图7 不同地区下的目标函数值比较Fig. 7 Object function values comparison in different regions

另外，通过所提出的CIF-OPT的优化算法，本文对缺失数据的耦合多光谱图像和全色图像进行了缺失数据的恢复，本实验的缺失数据发生在地区二的多光谱图像中，其中全色的图像的数据都是已知的，算法的具体结果如图8～9所示。通过观察经CIF-OPT算法恢复后的数据曲线可知，缺失数据为30%的耦合图像的数据恢复效果比缺失数据50%的恢复效果更好，即真实值与估计值之间的关系在缺失数据为30%时表现出更强的相关性，且线性斜率更接近于1。

通过图10可以看出，目标函数值并没有随着缺失数据百分比的增加而增加，即算法的最优值并没有随着缺失数据的增加而逐步变差。在缺失数据为15%和40%时，目标函数值更大一些；相反在缺失数据为40%以上，最优值反而降低。说明CIF-OPT算法对丢失数据方面具有强的恢复性，也体现了耦合图像对图像恢复算法的重要性。通过最优值的数值比较，也表明经过CIF-OPT算法后图像恢复效果并无太大的差别，但是存在个别奇异值。

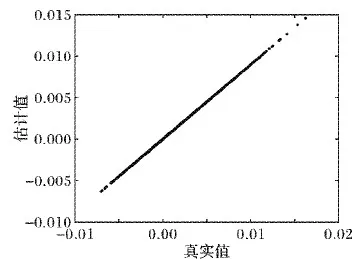
图8 缺失数据为30%的耦合图像的数据估计Fig. 8 Data estimation of coupled image with 30% missing data

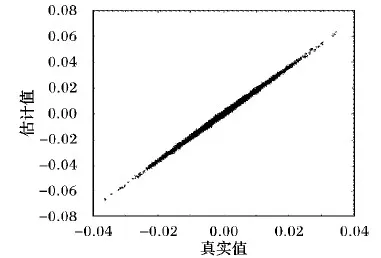
图9 缺失数据为50%的耦合图像的数据估计Fig. 9 Data estimation of coupled image with 50% missing data

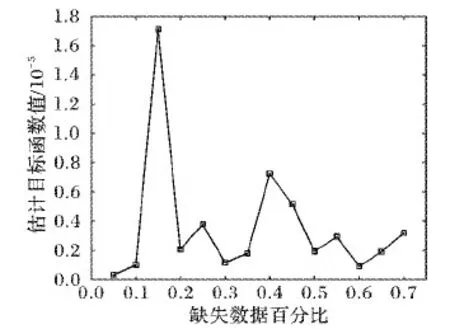
图10 不同缺失数据下的估计目标函数值Fig. 10 Estimation of function values with different missing data

本文分析不同缺失数据百分比下的估计误差，如图11所示，结果表明缺失值估计误差大致上呈现上升的趋势，即丢失的数据越少，经过恢复后的精确度越高，但是在缺失数据为20%和30%时出现了局部峰值，之后的误差随着缺失数据百分比而单调增加。因CIF-OPT算法主要通过耦合图像恢复原始缺失数据的图像，而耦合图像数据已知，故缺失数据百分比和估计误差在函数关系上并没有表现出强的相关性，而这也表明了CIF-OPT算法较强的数据恢复能力。

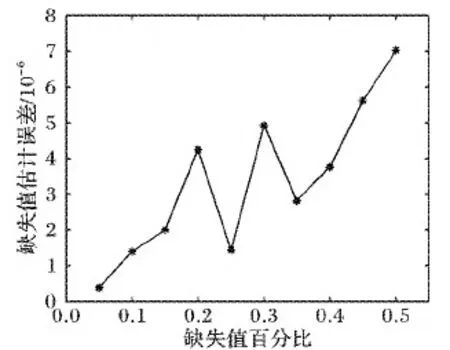
图11 不同缺失数据下的估计误差Fig. 11 Estimation error with different missing data

4 结语

本文提出针对耦合图像分解的CIF-OPT算法，主要利用耦合数据融合中的CMTF-OPT算法。相应的实验结果表明，不同噪声影响下耦合图像融合后的效果具有很强的鲁棒性，且融合效果优于CMTF-OPT算法，这说明该算法对耦合图像的分解具有可行性；同时，将耦合数据融合中改进后的CMTF算法(即ACMTF算法)应用到耦合图像中形成ACIF算法。

通过实验结果的对比发现，在噪声水平低的条件下，CIF-OPT比ACIF算法具有更好的融合效果，且算法收敛次数、估计误差均低于ACIF算法。针对其中缺失数据的图像，CIF-OPT算法可以通过与其耦合的图像在一定概率下对缺失数据的图像进行精确的恢复，图像恢复效果并不因缺失百分比的增加产生较大的差别，且估计误差也比较稳定。当然，虽然本文算法对图像数据能够进行较好的融合，但是在算法的过程中存在个别非正数据噪声，使得图像数据的显示存在一定的误差，因此，将来要将重点放在研究非负耦合张量之间的数据融合工作。