XLPE电缆的高频电容测量研究

国网鄂州供电公司检修分公司 杨 英 耿红杰 胡函武

高频电容的精确测量是高频介电特性研究的基础，但高频电容在测量中易受等效串联电感LS及边缘效应的影响而产生明显的实验误差。本文依据高频电容的等效电路，提出了精确计算高频电容的分析方法，并通过实验验证了该方法的合理性。

1.引言

聚合物介电特性的测量研究，在近年来兴起的 电气设备绝缘状态的无损诊断技术探索，局部放电信号在电缆中传播的衰变特性研究等诸多领域都具有重要的基础研究意义。而电缆介质复介电常数实部，虚部。因此，获取电缆样品精确的电容C值和电导G值是研究电缆介电特性的基础。但在高频电场下电容的测量存在较多的影响因素，导致高频电容的测量结果产生较大的误差，这对高频介电特性的研究造成了一定的影响。

本研究中采用阻抗分析仪测量电缆样品高频(1M～120MHz)电容C与电导G。在对电容C测量数据处理方面，通过对元件的等效电路进行深入分析，提出L-K法分析处理等效串联电感LS及边缘效应等因素对测量结果的影响，计算得到了精确的电容值。

2.实验样品及测量结果

图1为电导G和电容C的测量结果，从图中可看出，实验测量电导G的变化趋势与理论相似，电缆介质的损耗会随频率的增大先增大后减小。从图中可以看出电容C随频率的增大轻微减小，随后电容随频率的增大而不断增大。测量结果明显与理论预期变化规律相反。

因此，本文需要对电容C测量结果的异常现象予以充分研究和分析。

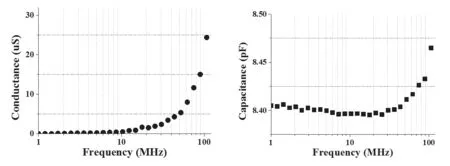
图1 电导G（左）和电容C（右）测量值随频率变化曲线

3.高频电容测量的中问题及分析方法

高频电容在测量中会受串联电感LS的影响而不断增大，同时由于本实验中电缆样品尺寸较短，由边缘效应引起的附加电容△C不可忽略。因此，本文提出图2所示的电缆样品高频电容测量的等效电路图。

3.1 高频电容测量影响因素

3.1.1 等效串联电感LS的影响

由图2所示的等效电路图，可分别得到式(1)和式(2)所示的等效电容Ce，也即电容真实值以及自谐振频率点f0(SRF)的表达式。

其中，Ce为电容真实值；C电容理论值；其中，△C为附加电容值；ω=2πf 为角频率；LS为等效串联电感。

本实验中样品电容在pF数量级，芯线电感在nH数量级，可估算高频段电容测量结果会随频率的增大而增大，因此电容测量结果与理论预期相反的变化趋势，是受样品导体芯线LS的影响导致的。

3.1.2 边缘效应的影响

电容测量中由边缘电场畸变引起的边缘效应，会使得电容测量结果偏大，本实验电缆样品长度较短，由边缘效应引起的附加电容△C不可忽略。电缆样品的边缘效应与样品边缘的形状、电极间距有关，而与样品的长度关联性较弱。故本实验中可认为不同长度电缆样品的△C相同。

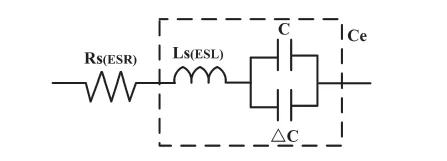
图2 电容样品实际等效电路图

3.2 高频电容理论分析——L-K法

通过对上述两点影响因素的分析，本文提出精确计算高频电容的分析方法——L-K法，消除上述两因素对电容测量的影响。

长度为l1和l2（其中l1≠l2）的两样品的电容理论值C1和C2，等效串联电感LS1和LS2均与长度成正比。因此，列写两样品电容Ce1和Ce2与其它参数的方程如式(3)所示。

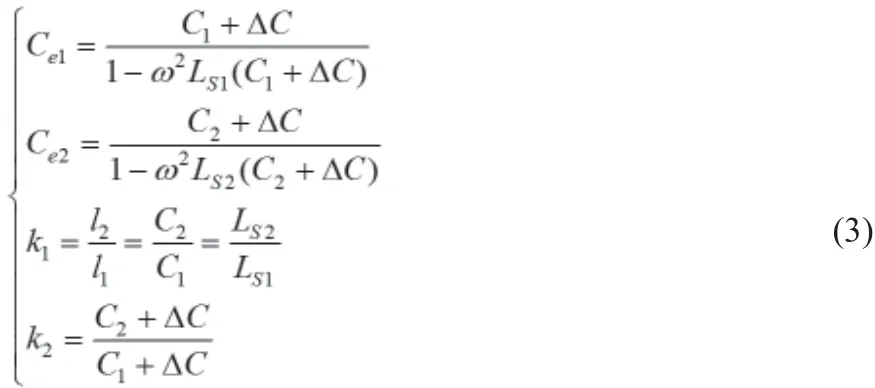
其中，k1为长度比；k2为并联附加电容△C后总电容的比值。

求解上述各参数关系方程(3)，即可解得式(4)所示LS1及C1及附加电容△C计算公式。

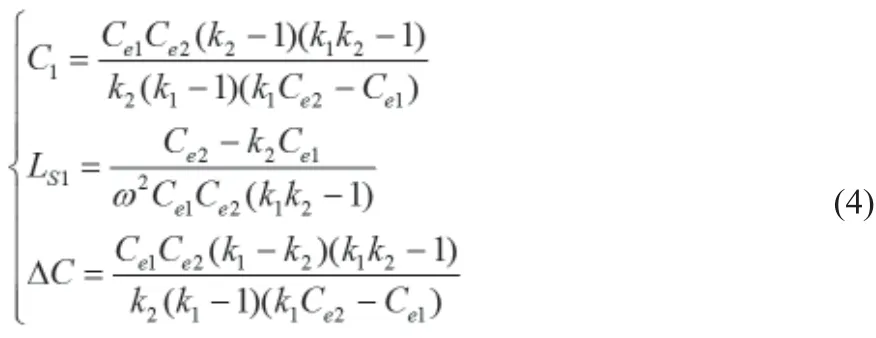
3.3 L-K法实验数据分析

实验测量两个不同长度的样品的电容值，两样品的尺寸规格如表1所示。依据上述理论分析方法，可对测量结果做如下分析。

表1 两个不同长度样品的尺寸

由于△C与C成一定的几何尺寸比例关系，故k2=(C2+△C)/(C1+△C)比值为常数。低频段(＜1MHz)，根据LS及电容的数量级可估算ω2LS(C+△C)数量级小于10-9。故可按式(1)近似认为Ce≈C+△C，因此可得k2=(C2+△C)/(C1+△C) ≈Ce2/ Ce1。则k2可选取低频段（如10k～100kHz）两样品电容测量值比值的平均值，因此可计算得到k2=1.838。代入式(4)即可求解获得#1样品的C1和LS1的计算结果。

图3为#1样品电容理论值C1与实验测量值Ce1的对比曲线。从图中可以看出，消除误差影响因素后，电容C1随频率的增大而不断减小，这与介电弛豫理论中偶极子极化在高频段随频率的增大而削弱，使得电容随频率增大而减小的预期规律相符。

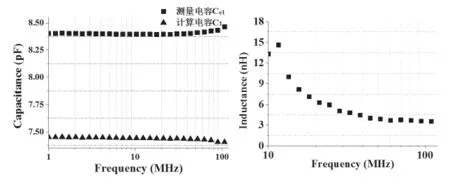
图3 电容理论值C1与测量值Ce1对比曲线

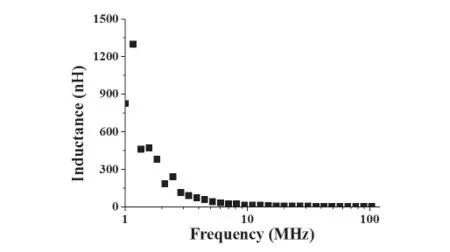
图4 等效串联电感LS1的计算值

图4所示为等效串联电感LS1的计算曲线，从图中可以看出，在≤10MHz频率范围内，LS1由1MHz处的1300nH减小至10MHz处的15nH，该频段内LS1数值变化率及波动性较大，这可能是由于电容测量值与真实值间误差所造成的。

在10M～120MHz范围内，随频率的增大，LS1由10MHz处的15nH与频率开方呈反比减小至120MHz处的3.5nH，且波动性不断减小，并趋于平滑。这是由于根据式(4)中LS1计算公式，随频率的增大，Ce1和Ce2的测量值与真实值间的误差对电感计算值的影响将与频率平方成反比减小，使高频段LS1的精确度提高，对应高频段电容理论值C1的有效性大大提高。

4.结论

对不同长度样品电容值进行测量，并采用L-K法进行处理，根据式(4)可计算得到电容理论值C、等效串联电感LS以及边缘效应附加电容值△C。

等效串联电感LS计算值在较低频段(≤10MHz)受电容测量值与真实值之间的误差影响，可能出现一定幅度的波动及数值偏大的现象，但低频段C的受LS影响较小，此频段内可忽略LS对电容测量的影响。

在高频段(＞10MHz)，由电容测量与真实值之间的误差将成频率平方比降低，因此LS的计算值具有非常高的精度，故计算得到的电容C也具有较高的有效性。