一种基于样本熵的雷达辐射源信号分选

西南交通大学电气工程学院 徐 赛 金炜东

针对现有方法分选准确率低以及对噪声敏感的问题，提出一种新的雷达辐射源信号分选的方法，实现了低信噪比下雷达辐射源信号的高正确率分选。对接收到的雷达辐射源信号进行Fourier变换和归一化处理；然后对预处理后的信号重采样，提取信号的样本熵和功率谱熵特征；最后运用SVM实现6类雷达辐射源信号的分选。由仿真实验结果可知，当信噪比在0dB以下时，6类雷达辐射源信号的平均正确识别率最低为92.03%；当信噪比为10dB时，6类信号可以达到完全分离，验证了所提方法的有效性和可行性。

1 概述

随着现代雷达技术的不断发展，电子对抗环境日趋复杂与密集，新体制雷达不断出现以及信号参数不断变化，因此提取雷达特征中的常规参数（如CF、PW、AOA、PA和TOA）等传统方法已难以适用于现代雷达辐射源信号分选。雷达信号最具特色的参数之一是脉内特征，在此研究趋势之下国内外的数名学者针对脉内特征提取的工作做了不少，并且提出很多有效的方法来提取雷达辐射源信号的脉内特征，如相位差分法（RTK）、线核聚类、调制域分析法、数字中频法、小波变换法、复杂度特征以及相像系数（RC）等。以上脉内特征参数在雷达辐射源信号的分选识别方法在应用中已取得了一定的成效（韩俊,何明浩,朱振波,等.基于复杂度特征的未知雷达辐射源信号分选[J].电子与信息学报,2009,31(11):2552-2556;刘凯,韩嘉宾,黄青华.基于改进相像系数和奇异谱熵的雷达信号分选[J].现代雷达,2015,7,37(09):80-85;刘生锋,严勇,陆建兵.随机相位编码在多普勒天气雷达中的应用[J].现代雷达,2014,36(06):26-28+34;陈婷,陈卫.基于覆盖算法的SVM雷达辐射源识别[J].计算机工程,2011,37(10):179-181;Lipeng G,Juan J,Yuning Z.Sorting and recognition of in tra-pulse modulation signals based on FRET[C].//2012 5thGlobal Symposium on MillimeterWaves.Harbin,China;IEEE Press,2012:494-497;于新星,王永.基于在线核聚类的雷达信号分选方法[J].计算机工程,2012,38(03):270-272+275）。上述的雷达信号分选方法是在一定的信噪比条件下实现的，但是在信噪比较低或在低于0dB的情况下，这些方法的分选正确率不高，难以满足当今战场上的要求。基于样本熵的雷达辐射源信号分选的新方法，在较低的信噪比下甚至在信噪比为负的条件下，提取出样本熵和功率谱熵特征，并用SVM自动分类识别。

2 熵特征提取及比较

2.1 样本熵的介绍

样本熵（SampEn）是Richman等研究发展的一种有别于近似熵的不计数自身匹配的统计量，是对于近似熵算法的改进（Richman J S,Moorman J R.Physiologica time-series analysis using approximate entropy and sample entropy[J].Am J Physio:Heart Circ Physio,2000,278(6):2039-2049）。雷达信号是一种叠加信号，由需要识别的有用信号和随机的噪声组成。因此在雷达信号识别上具有一定的不确定性。这种在识别上的不确定性不仅与事件发生的概率(SNR的范围区间)之间相关，同时与所判断事件本身具有某些特性的关联程度相关，这与熵的性质部分重合。因此，本文经过不同的熵特征比较实验后，说明样本熵对雷达辐射源信号的复杂性描述较好。

结合雷达辐射源信号识别背景，以下给出了SampEn的算法实现步骤（Alcaraz R,Rieta J J.A review on sample entropy applications for the non-invasive analysis of atrial fibrillation electrocardiograms[J].Biomedical Signal Processing and Control,2010,5(1):1-14）：

信号重采样：针对雷达辐射源信号长度对计算速率的影响，需要对进行预处理之后的雷达辐射源信号进行信号重采样，经过重采样后得到的雷达辐射源信号为（N为雷达辐射源信号重采样后序列的长度）。

SampEn算法的具体步骤如下：

Step1 把重采样后的雷达信号按序号组成一组维数为m的向量序列，。这些向量序列Um代表的是从第i点开始的m个连续的采样信号u的值。

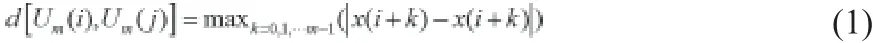
Step4 增加到维数到 m+1，计算向量序列Um(i )与Um(j )距离中其值小于等于r的向量序列个数，记为Bi。 且定义B(m)(r)为：

综上所述，A(m)(r)为两个向量序列在相似容限r设定下匹配m个点所得到的概率。而B(m)(r)为两个向量序列匹配 m+1个点所得到的概率。因此将样本熵定义为：

SampEn的值与参数m和r的选择有关，根据Pincus研究的结果（Pincus S M.Assessing serial irregularity and its implications for health[J].Annals of the New York Academy of Sciences,2001,954(1):245-267），通常取，，STD（标准偏差）作为处理后的信号序列的标准差。设定后的样本熵统计特性较为合理。通过多次进行仿真实验，最终在计算雷达辐射源信号的样本熵时，设定参数值，。

2.2 样本熵与近似熵的比较

由图1可以看出，相同的信噪比下，同一信号的SampEn值小于ApEn值。通过比较SampEn和ApEn可知，SampEn具备一些优点（[10]刘慧,和卫星,陈晓平.生物时间序列的近似熵和样本熵方法比较[J].仪器仪表学报,2004,25(z1):806-807+812;[11]Chen X,Solomon I,Chon K.Comparison of the use of approximate entropy and sample entropy:applications to neural respiratory signal[C]//Conference proceeding.Annual International Conference of the IEEE Engineering in Medicine and Biology Society.IEEE Engineering in Medicine and Biology Society.Annual Conference,2004,4:4212-4215）：在实际应用中，由于样本熵具有在比较短的时间序列数据中可以得到稳定的估计数值的特性，因此具有较好的抗干扰和抗噪声能力。并且在上文所述中，样本熵适用于由随机成分（信号噪声）和确定性成分（待识别雷达信号）组成的混合信号，具有优于简单统计参数(如均值、方差、标准差等)的分析效果。因此，本文选用SampEn作为特征雷达信号分类。

图1 Apen与SampEn的比较

2.3 功率谱熵

功率谱熵（SE）的定义（Powell,G.E.;Percival,I.C.A spectral entropy method for distinguishing regular and irregular motions for Hamiltonian systems[J].Phys.Math.Gen,1979,12(11):2053-2071）：设一组离散的时间序列信号（M为信号序列的长度），其采样频率为fs，采样点数为N。Flourier变换得到X(wi)，为角频率，则功率谱密度为：

考虑到功率谱的的对称性，只取Flourier变换的一半的分量点，从而提高了计算效率。接着将功率谱密度P(wi)进行归一化处理后，得到功率谱的概率密度分布函数 Pi。 Pi能反映功率谱在频率fi上所占整个谱中的百分比情况，即：

为定义功率谱熵需要依据信息熵的概念，即离散随机事件的出现概率，因此对功率谱熵定义如下：

在公式(7)中，为判断在频率f上的时间不确定性量度问题，可以通过功率谱熵值H进行解释。因此功率谱熵值H可为判断系统本身复杂性的量度。如果所研究的系统本身的不确定性或复杂性越大，那么得到的谱熵也就越大；反之亦然。因此，本文选择功率谱熵作为描述雷达信号的复杂性参数指标。

2.4 雷达信号分选流程

综上分析，对接收到的雷达信号按图2步骤处理，以实现分选。

图2 雷达信号分选熵流程图

3 仿真实验结果与分析

3.1 仿真条件

为了验证本算法的有效性，本文对常规信号(CW)、二相编码信号(BPSK)、线性调频信号(LFM)、四相编码信号(QPSK)、非线性调频信号(NLFM)和频率编码信号（FSK）这6类雷达辐射源信号进行脉内调制信号的特征提取和仿真实验。信号载频为8MHz，脉宽为1μs，采样率为80MHz。CW为普通的正弦信号，LFM的带宽为8MHz。BPSK的相位编码规律为13位随机巴克码，QPSK采用的相位编码规律为16位的Frank码，FSK的相位编码规律为13位随机巴克码。NLFM为非线性正弦信号。

在SNR范围为-10dB～10dB的情况下，每类信号分别产生100个样本，每个样本采样1024个数据点。

3.2 实验分析

在SNR范围为-10dB～10dB的情况下，先分别求取6类雷达辐射源信号的样本熵和功率谱熵值。在SNR(只考虑脉内噪声)范围之内，设定步长为5dB且输出100个样本；最终仿真输出得到6种雷达辐射源信号的500个样本；为了更加直观地反映上述6种雷达辐射源信号熵特征的分布情况，本文针对6种雷达辐射源信号在不同SNR点上分别提取100个特征样本，总共得到500个特征样本。特征分布图如图3所示，在-10dB时，BPSK、NLFM和FSK熵特征有部分交叠重合；如图4所示为BPSK与NLFM交叠重合情况；如图5所示为BPSK与FSK交叠重合的情况；如图6所示为NLFM与FSK交叠重合情况。如图7所示，当SNR为10dB时，各类雷达信号之间没有交叠，能达到完全分离。

图3 -10dB雷达信号熵特征分布

图4 -10dB BPSK、NLFM的熵特征分布图

图5 -10dB BPSK、FSK的熵特征分布图

图6 -10dB NLFM、FSK的熵特征分布图

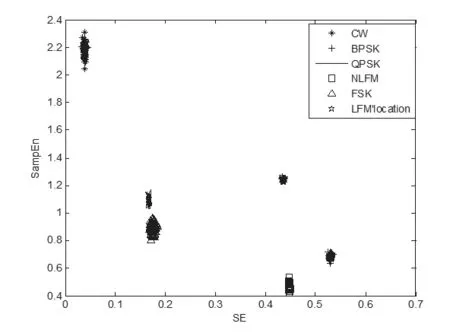
图7 10dB雷达信号的熵特征分布图

在实验中，使用SVM对样本进行分类。为了验证该算法的有效性，每类信号在不同信噪比下分别产生100个信号点，每类信号随机产生70个训练集样本训练SVM分类器，然后再用测试集样本去测试已训练的样本，根据Monte Carlo方法，实验的统计结果如表1所示。

表1 6类雷达信号分选的正确率（%）

正如表1所示，由于BPSK、NLFM和FSK熵特征部分交叠重合导致信号分选正确率降低的情况得到了验证。从从图6可以看出，NLFM和FSK的熵特征交叠重合情况严重，所以分选结果显示6类信号分选正确率为只有92.03%。

从表1可知，当SNR为10dB以上的情况下，6类雷达辐射源信号的分选正确率均为100%；随着SNR参数设定下降，其分选准确率也随之下降；SNR达到5dB时，6种调制方式的信号最低的分选正确率仍然能达到98.48%；当SNR达到-10dB时，其平均分选的正确率仍能达到92.03%左右，其分选正确率较高。

3.3 方法比较

文献（梁华东,徐庆.熵特征在雷达信号分选中的应用[J].空军预警学院学报,2015,29(01):7-12）提出了维格纳分布空间和双谱空间，用于雷达信号分选。文献（韩俊,何明浩,朱振波,等.基于复杂度特征的未知雷达辐射源信号分选[J].电子与信息学报,2009,31(11):2552-2556;）提出了复杂度特征，即盒维数和稀疏性，用于雷达信号分选。为进一步验本文方法的性能，分别采用本文方法以及文献（梁华东,徐庆.熵特征在雷达信号分选中的应用[J].空军预警学院学报,2015,29(01):7-12）方法和文献（韩俊,何明浩,朱振波,等.基于复杂度特征的未知雷达辐射源信号分选[J].电子与信息学报,2009,31(11):2552-2556;）方法对未知雷达信号进行分选，并比较分选正确率。图8为3种方法的分选结果。

图8 3种方法分选正确率

本文算法的准确率远远高于文献（韩俊,何明浩,朱振波,等.基于复杂度特征的未知雷达辐射源信号分选[J].电子与信息学报,2009,31(11):2552-2556;）的准确率。虽然在0dB～3dB之间，本文算法的正确率低于文献（梁华东,徐庆.熵特征在雷达信号分选中的应用[J].空军预警学院学报,2015,29(01):7-12），但当SNR达到3dB以上时，分选正确率均高于文献（梁华东,徐庆.熵特征在雷达信号分选中的应用[J].空军预警学院学报,2015,29(01):7-12）和文献（韩俊,何明浩,朱振波,等.基于复杂度特征的未知雷达辐射源信号分选[J].电子与信息学报,2009,31(11):2552-2556;）。在10dB时，分选正确率已经达到100%，其正确率比文献（梁华东,徐庆.熵特征在雷达信号分选中的应用[J].空军预警学院学报,2015,29(01):7-12）高0.3%，比文献[1]高2%。同时，当信噪比为0dB以下的时候，平均正确率最低为92.03%，则本文算法整体的分选正确率高于文献（韩俊,何明浩,朱振波,等.基于复杂度特征的未知雷达辐射源信号分选[J].电子与信息学报,2009,31(11):2552-2556;）、（梁华东,徐庆.熵特征在雷达信号分选中的应用[J].空军预警学院学报,2015,29(01):7-12）。因此，针对不同调制类型的信号，本文方法整体的分选正确率最高。

4 结束语

本文主要研究内容为在一定SNR条件下的雷达辐射源信号的特征提取和识别问题。通过对6种典型雷达辐射源信号的样本熵和功率谱熵特征提取以及SVM进行分类。仿真实验和方法对比表明，信噪比在0dB以下的情况下，信号NLFM与FSK重叠严重，单种信号的识别率为83%左右，有待于探究这两类信号的分选。但整体识别正确率达到92%以上，分选效果优于文献（张葛祥,胡来招,金炜东.基于熵特征的雷达辐射源信号识别[J].电波科学学报,2005,20(04):30-35），也就证明了样本熵要优于近似熵。在10dB的条件下，6类信号可以达到完全分离。 从而表明该方法具有有效性和一定的参考价值。