NSCT域内结合相位一致性激励PCNN的多聚焦图像融合
刘 栋,周冬明,聂仁灿,侯瑞超
(云南大学 信息学院,昆明 650500)(*通信作者电子邮箱zhoudm@ynu.edu.cn)
0 引言
多聚焦图像融合是图像处理领域的一个重要分支。就目前而言,该技术已被广泛应用于计算机视觉、目标识别和人工智能等多个领域。在使用光学镜头拍摄照片时,受到光学镜头聚焦能力的限制,大多数关于同一场景的图片会出现不同的焦点,这就导致图片的某些清晰的、细节的信息只能出现在聚焦的区域中,而非聚焦区域的图像信息是不易被人眼直接观测到的[1]。因此,多聚焦图像融合技术的关键在于准确提取多聚焦源图像中的有用信息,来获得一张精度更高、更加清晰、更利于人眼观察的图片。
多聚焦图像融合技术有效地消除了现代光学镜头景深有限的缺陷,提高了图像的精度,并能够消除图像像素间的冗余信息。目前,在该领域使用较多的方法是基于多尺度变换的图像融合方法,如基于金字塔变换[2]、离散小波变换[3]、基于非下采样轮廓波变换(Non-Subsampled Contourlet Transform, NSCT)[4]和非下采样剪切波变换(Non-Subsampled Shearlet Transform, NSST)[5]的图像多尺度分解算法。其中,金字塔变换缺乏方向性,离散小波变换也不能有效地反映图像的曲线与边缘信息[6],NSCT和NSST又忽略了图像的空间一致性[7]。为了获得更好的视觉感知并充分利用图像空间信息,一些结合脉冲耦合神经网络(Pulse Coupled Neural Network, PCNN)的方法得到广泛的应用,如NSCT-PCNN[8]、NSST-PCNN[9]等,然而这些方法在对图像不同区域的像素进行处理时,容易受到噪声的影响并且不能很好地保留源图像的一些边缘与细节结构信息。
针对上述的一些算法缺陷,本文提出了一种在NSCT域内通过计算空间频率(Spatial Frequency, SF)和相位一致性(Phase Congruency, PC)来驱动PCNN神经元进行多聚焦图像融合的算法。相位一致性作为图像的一种特征,其值不会因为图像的亮度、对比度和光照强度的变化而受到影响,这一特点符合人类视觉特性。有研究表明,人类眼睛感觉到的图像特征往往位于PC值高的点处[10],同时,相位一致性对噪声有较强的鲁棒性,可以减少噪声和平滑图像,而且在同一阶段的图像特征中包含许多频率成分,如边缘状和角状特征。空间频率作为图像的梯度特征,它反映了一幅图像的总体活跃程度,图像空间频率特征的值越大,表明图像越活跃、越清晰[11]。因此,本文提出的根据图像高低频特性来分别计算其SF和PC值的融合规则能够很好地对源图像的聚焦区域进行高精度的提取,有效地避免了融合图像中目标边缘及细节信息缺失的现象,达到了一个较好的融合效果。
1 简化PCNN模型
为了简化计算过程,一种简化的脉冲耦合神经网络模型(Simplified PCNN, S-PCNN)[12]被用于本文方法中。与传统PCNN模型相同,S-PCNN模型由接收域(receptive field)、调制域(modulation field)和脉冲发生器(pulse generator)三部分组成,如图1所示,在S-PCNN模型中,每一个神经元都唯一对应着一个图像像素点。S-PCNN的数学模型可由式(1)~(5)来表示:
Fij(n)=Sij
(1)
(2)
Uij(n)=Fij(n)(1+βLij(n))
(3)
θij(n)=exp(-αθ)θij(n-1)+VθYij(n-1)
(4)
(5)
其中:i和j表示神经元(或图像像素点)的位置。神经元(i,j)在接收域中接收到来自其邻域神经元(k,l)的输入脉冲,并通过反馈通道Lij进行传输,该通道的衰减幅度为VL,相邻的神经元之间以突触链接权Wijkl相链接,输入通道Fij仅与外部激励Sij有关;在调制域中,通过双通道的内部调制得到神经元的内部状态Uij,其链接强度为β;在脉冲发生器中,当Uij的值大于阈值θij时,触发神经元点火产生脉冲,然后阈值会以指数方式进行衰减,αθ为其衰减指数,Yij为输出脉冲。基于PCNN的图像融合算法步骤[13]如下:
1)当Uij>θij时,触发PCNN神经元点火,此时,Yij=1;
2)一旦位于(i,j)处的神经元点火成功,阈值θij的值会立即增大,然后随着时间的流逝呈现指数级的衰减;
3)当Uij≤θij时,神经元停止点火,同时,在神经元点火过程中会产生一个脉冲序列信号;
4)由于PCNN中每个神经元都与其周围相邻的神经元相互联系,因此一个已被点火的神经元会驱动其相邻的神经元进行点火。
这样一来,当PCNN中的神经元被其相邻的神经元触发点火,整个神经网络中的神经元将会处于激活状态,来进行图像融合的处理。

图1 S-PCNN 模型Fig. 1 S-PCNN model
2 图像多尺度分解
近年来,利用NSCT对图像进行多尺度分解,在图像融合领域的优越性已被国内外许多学者的研究证明。NSCT作为一个由轮廓波变换(Contourlet Transform, CT)改进而来的二维图像处理工具,其中包含了非下采样金字塔滤波器(Non-Subsampled Pyramid, NSP)和非下采样方向滤波器(Non-Subsampled Directional Filter Bank, NSDFB),如图2所示。与传统的轮廓波变换相比,经NSCT得到的融合图像能够避免不必要的失真,并且能获得更好的频率选择性、规律性和位移不变性。其中:NSP是一个双通道滤波器组,NSDFB是一个扇形滤波器组,源图像经过这两个滤波器组,将被分解为与源图像同大小的低频子带图(低频系数)和带通子带图(高频系数)[14],源图像中有效信息的近似分量和大量的细节与结构特征分量信息分别包含在低频和高频子带中。

图2 基于NSCT的图像多尺度分解框架Fig. 2 Decomposition framework of NSCT
因此,不同的融合规则将分别应用于低频系数和高频系数的融合,最后通过逆NSCT对融合后的低频系数和高频系数进行处理,以得到一幅包含两幅源图像有效信息并且所有对象都清晰的融合图像。
3 融合规则
3.1 高频系数融合规则
图像空间频率是与图像梯度值相关的一种图像特征,它反映了图像的活跃程度[15],其值越大,图像越清晰;反之图像越模糊。本文将计算高频子带的空间频率值,作为PCNN的外部激励输入,以获得PCNN神经元点火脉冲序列,对高频子带进行融合,其值可由图像行频率(Row Frequency, RF)与列频率(Column Frequency, CF)计算而来:
(6)
(7)
(8)
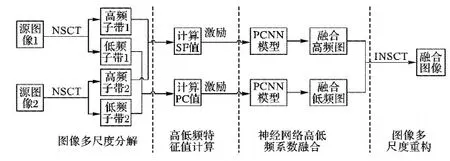
图3 本文算法框架Fig. 3 Framework of the proposed image fusion algorithm
3.2 低频系数融合规则
图像相位一致性是图像低水平的不变形属性,同时,相位一致性特征还为相位校准模式的协议提供了一种量化方法[16]。Oppenheim等[17]通过大量实验已经证明图像的许多重要特征在相位图中可以明确地被识别出来,然而这些特征却不能在频谱图中被很好地识别,由此还发现图像傅里叶相位包含了关于图像结构和特征的重要信息。Kovesi等[18]指出,图像的特征往往出现在图像相位一致性值最大的点处,同时,考虑到图像相位一致性特征对图像像素强度映射和光照对比度变化具有不变性,本文将图像PC值作为PCNN的外部激励输入以进行图像低频系数的融合,Kovesi[19-20]提出了一种改进的相位一致性计算方法来避免可能出现的缺点:
(9)
其中:
(10)

(11)
Wo(x)是滤波响应权重函数;N是涉及到的总的尺度数;Amax(x)是滤波器组在点x处响应的最大幅度值;Ano(x)为尺度n处的振幅,当符号“⎣」”中的值为正时,其结果等于自己本身,否则结果为0;ε是一个极小的常数,用于避免分母为零的情况;To是对噪声响应的估计。相位偏差值表示为:
(12)
在这个改进的相位一致性模型中,Kovesi[20]利用了log Gabor函数来计算一幅图像的相位一致性值[21],与传统的Gabor函数不同,log Gabor函数在对数频率尺度上是一个高斯函数,因此log Gabor函数在对数频率尺度上是对称的,并且它在构造出任意大带宽滤波器的同时,能够始终保持在偶对称滤波器中有一个零直流分量,这是Gabor函数不具备的功能,此外,log Gabor函数符合人类视觉系统在对数频率尺度下细胞反应对称的特性[22]。由文献[23]可知,log Gabor函数的一维数学表达式为:

(13)
其中:ω0为中心频率;β/ω0根据不同的ω0值取不同的常数以获得不同频程带宽。
4 本文算法
SF-PCNN与PC-PCNN分别作为高频系数与低频系数的融合规则来驱动PCNN神经元,利用PCNN神经元点火后阈值自动设置的特性来激活整个神经网络以进行多聚焦图像融合。本文算法中,分别计算两幅源图像分解后同一位置处像素点的高频分量的SF值与低频分量的PC值,选取值较大的点作为PCNN外部激励以获得融合后的低频和高频图像,即:
(14)
(15)
其中:上标1和2分别表示源图像1和2的高低频分量。本文算法结构如图3所示。
5 实验结果与分析


表1 对比实验结果客观评价指标Table.1 Performance comparison of different fusion algorithms

图4 多聚焦图像融合实验源图像Fig. 4 Three couples of multi-focus fusion source images

图5 Clock融合对比实验结果Fig. 5 Experimental result of Clock fusion

图6 Pepsi融合对比实验结果Fig. 6 Experimental result of Pepsi fusion
实验环境为:Windows 10,Intel Corel CPU 3.00 GHz,RAM 4 GB, Matlab R2016a。
在表1所示的客观评价指标数值中,本文算法的各项指标几乎全部大于4种基于多尺度变换的经典算法,与近年来的新算法相比,3组多聚焦实验数据共15个测试结果中,近一半的数据结果是优于这3种算法的,其余结果与最大值相接近(如Lab数据集的QAB/F指标:最大值为0.75,本文算法的值为0.73,差值仅为0.02)。同时,如图8~13的差值图的方框所示,可以清楚发现对比算法的差值图中所包含的源图像的清晰区域的痕迹较多;特别地,实验数据Lab的左右聚焦区域细节信息相差较大,当对Lab的左聚焦区域(时钟)进行提取融合后,各算法的融合效果相差无几,如图12所示;当对右聚焦区域(人物)进行提取融合后,可以清楚发现所提算法对人物细节信息的提取要明显优于其余7种对比算法,如图13所示。

图7 Lab融合对比实验结果Fig. 7 Experimental result of Lab fusion

图8 Clock融合结果与Clock1的差值图Fig. 8 Difference maps between Fig.5 and Clock1

图9 Clock融合结果与Clock2的差值图Fig. 9 Difference maps between Fig.5 and Clock2

图10 Pepsi融合结果与Pepsi1的值图Fig. 10 Difference maps between Fig.6 and Pepsi1

图11 Pepsi融合结果与Pepsi2的值图Fig. 11 Difference maps between Fig.6 and Pepsi2

图12 Lab融合结果与Lab1的值图Fig. 12 Difference maps between Fig.7 and Lab1

图13 Lab融合结果与Lab2的值图Fig. 13 Difference maps between Fig.7 and Lab2
6 结语
综合相位一致性对图像亮度、对比度具有不变性,以及空间频率对图像梯度信息的表达,利用脉冲耦合神经网络的生物学特点以及人眼的视觉特性,提出了一种NSCT域内结合相位一致性与空间频率激励PCNN的多聚焦图像融合算法。首先对多聚焦图像进行多尺度分解,根据图像高低频系数的特点,分别选取SF和PC结合PCNN作为图像高低频系数的融合准则,最后通过逆NSCT算法,重构得到一幅所有物体都清晰的融合图像。实验测得的客观评价指标和实验差值图充分表明所提算法能够将源图像的聚焦区域更加完整的、更有效地提取到融合图像中,其融合效果明显优于其余对比算法,这意味着本文算法在多聚焦图像融合方面具有一定的优越性。

