基于改进模糊熵和证据推理的多属性决策方法
熊宁欣,王应明
(福州大学 经济与管理学院,福州 350116)(*通信作者电子邮箱531626142@qq.com)
0 引言
证据推理(Evidential Reasoning,ER)方法作为处理不确定性多属性决策问题的描绘工具,受到了国内外广大学者的重视,目前已成功应用于决策分析[1]、双边匹配[2]、绩效评估[3]、系统预测[4]等领域。证据推理方法是在证据理论(Dempster-Shafer Theory, DST)和决策理论的基础上经历20多年的历程发展而来的。其中证据理论由Dempster[5]在1967年首次提出,他的学生Shafer[6]对该理论进行了系统的研究,最终形成了目前的证据理论。它是一种能够对证据进行融合的数学工具,在处理不确定性多源信息的过程中起了重要作用。1994年,Yang等[7]在证据理论的基础上,结合评估分析模型,首次将证据理论引入多属性决策领域,提出了不确定情况下的证据推理方法,并给出了ER证据组合规则。2002年,Yang等[8]研究开发了满足四个合成公理的证据推理算法,即递归证据推理算法。2006年,Wang等[9]在递归证据推理算法的基础上,进一步提出计算更加简便的解析证据推理算法。至此,奠定了证据推理方法的理论基础,验证了该方法的有效性。
随着研究的深入,证据推理方法在识别框架的构建、评估信息转换、证据融合规则等方面的理论体系已逐步完善,并取得了一定的研究成果,但仍面临着证据权重难以获取及量化的问题。目前,在基于证据推理的客观赋权法研究中,主要存在以下三类研究:第一类从解决证据冲突的角度出发,根据Jousselme等[10]给出的证据距离定义,建立最小化理想距离模型以确定属性权重。如王小艺等[11]通过建立各个加权证据与期望证据之间的距离最优化模型,获得最优的证据权重分配。陆文星等[12]提出一种基于证据距离的客观权重确定方法,使证据体与系统中其他证据的总距离达到最小以确定权重。第二类方法主要是利用属性权重的不完全信息建立非线性规划模型求解权重。王坚强[13]结合属性权重和等级效用的不完全确定信息建立非线性规划模型,利用遗传算法求解得到各属性的权重。朱建军等[14]结合原始专家信息,建立了基于专家意见偏差最小的非线性优化模型计算属性权重。第三类则是基于信息熵方法确定熵权。尹德进等[15]将定量、定性、模糊和不完全等各种特征的信息统一转换到信度框架下,通过不确定信息熵模型求取各属性的熵权值。Bao等[16]通过对属性权重与熵、交叉熵、期望值三个指标之间进行相关性分析,在权重不完全且未知的情况下建立了属性权重的识别优化模型求解权重。
在已有的权重求解方法中,通常无法充分利用证据推理信度框架中的原始信息,从而很大程度影响了决策过程的客观性。本文提出一种基于改进模糊熵和证据推理的不确定多属性决策方法,更加客观地确定属性权重。首先,定义一种基于三角函数的改进模糊熵公式,能够刻画属性的模糊性及属性间信息量的差异程度,并能够同时处理属性权重完全未知和属性权重信息部分已知两种情况。其次,针对属性权重完全未知的情况,结合模糊熵和熵权法的基本思想计算属性权重;针对属性权重信息部分已知的情况,定义加权模糊熵,建立期望模糊熵最小的线性规划模型求解最优属性权重。最后,利用证据推理算法融合属性值,结合期望效用理论对方案进行优劣排序,以实例说明该方法的可行性、有效性。
1 证据推理算法
1.1 证据理论概述


则称m为基本可信度分配(Basic Probability Assignment,BPA)或信念结构。设两个独立证据A和B,按照Dempster-Shafer组合规则融合后的结果为:
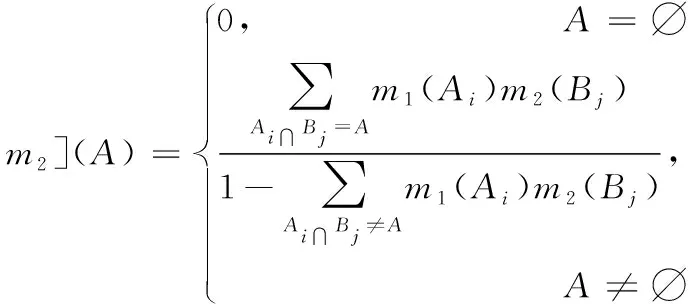
1.2 基于证据推理的多属性决策问题描述
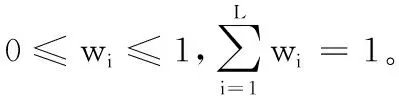
S(ei(al))={(Hn,βn,i(al))|n=1,2,…,N;
i=1,2,…,L;l=1,2,…,M}
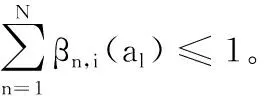
1.3 证据推理融合算法
在证据推理框架下,所有基本属性的信度值βn,i(al)必须使用Dempster-Shafer组合规则进行信息融合获得方案综合分布评价信度βn(al)。
令mn,i(al)为基本概率分配函数,表示方案al在广义属性y下属于评价等级Hn的信任度。
mn,i(al)=wiβn,i(al)
(1)
令mH,i(al)为未分配概率指派函数,表示对于广义属性y,方案al在属性ei下未分配给任何评价等级Hn的信任度。
(2)
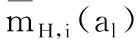
(3)

(4)
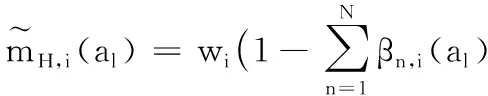
(5)
证据推理通过建立广义属性综合评价与基本属性原始评价之间的非线性关系,将各个证据进行逐步融合,不断循环直至将所有证据融合完毕。首先假定:
mn,I(1)=mn,1
mH,I(1)=mH,1
具体融合算法[8]如下:
{Hn}:mn,I(i+1)=KI(i+1)[mn,I(i)mn,i+1+mH,I(i)mn,i+1+
mn,I(i)mH,i+1]
(6)
(7)
(8)
(9)
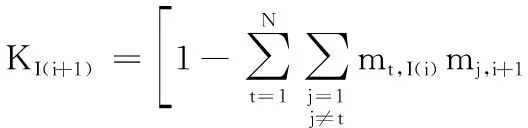
(10)
其中:I(i+1)表示融合i+1个基本属性;KI(i+1)表示第i次集结时的归一化系数。在所有基本属性评估信息集结完成后,使用如下标准化过程逆向转换为方案的广义属性综合信任度:
(11)
(12)
其中:βn表示为方案al分配给评价等级Hn的信任度;βH表示广义评估中的未分配信度。因此,方案ai的广义分布评价为:
S(y)={(Hn,βn(al))|n=1,2,…,N;l=1,2,…,M}
其中:S(y)表示方案ai在广义属性y下被评为等级Hn的支持度为βn。
2 基于三角函数的改进模糊熵公式
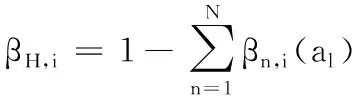
(13)
其中:En表示信任度框架下方案al在属性ei下被评为不同评价等级的信任度偏差。定义证据推理信度决策矩阵框架下,基于三角函数的模糊熵公式为:
(14)
从式(14)可以看出,信度框架下基于三角函数的模糊熵公式不仅包含了信任偏差度,且包含因无知而引起的不确定指数,能够较好地刻画信息不确定程度。
定义1 称函数E(A)为模糊熵,若其满足如下拓展的公理化要求:
条件1E(A)=0当且仅当A为传统精确集;
条件2E(A)=1当且仅当对于每一个βn,i(al)都有βn,i(al)=βn, j(al)成立;
条件3E(A)=E(Ac);
条件4 若βH,A=βH,B时,有En(A)≤En(B),或者当En(A)=En(B)时,有βH,A≥βH,B,均有E(A)≥E(B)。
定理1 由式(14)定义的E是一个模糊熵。
证明 要证明由式(14)定义的E是一个模糊熵,只需证明其满足定义1中的四个条件。

对于条件3,由于(En)C=En,显然有E(A)=E(Ac)。
对于条件4,改进的模糊熵是关于En的减函数,关于βH,i的增函数。βH,A=βH,B时,若En(A)≤En(B),表示A中支持各等级的证据越相近,或者当En(A)=En(B)时, 若βH,A≥βH,B,表示A中的证据更少,均有E(A)≥E(B)。
由此,可进一步总结证据推理框架下的三角模糊熵具有的几点特点:
1)显然,0≤E(s(ei(al)))≤1恒成立。
2)当n=1,β1,1(al)=1时,模糊熵取最小值0。
3)对某个S(ei(al))而言,若En=0且n>1,模糊熵取最大值1,意味着方案al在属性ei下被评为各评价等级的信任度是相等的,即支持不同评价等级的证据一样多。
4)n值越大,表示方案al在属性ei下支持各评价等级的证据越分散。
5)En的值越小,方案al在属性ei下支持各评价等级的偏差越小,意味着支持各评价等级的证据越相近,从而模糊性增加,模糊熵值越大。
6)βH,i的值越小,表示因无知而引起的不确定信息越少,支持各评价等级的证据越多,模糊熵相应减小。
3 本文方法
针对基于证据推理的不确定多属性决策问题,对于基本属性与广义属性评价集不一致的情况,首先对模糊决策信息进行信息技术转化,实现从基本评价到广义分布评价的统一形式。其次,本文开发一种适用于证据推理分布信度决策矩阵的改进模糊熵公式,能够处理属性权重完全未知以及属性权重信息部分已知的两种情况。基于改进模糊熵和证据推理的多属性决策方法具体步骤如下。
步骤1 转化决策信息,构建信度决策矩阵。
证据推理决策框架采用分布式信度结构表示,属性值可以用决策者主观定性评价表示,也可通过定量评估确定,最后转换为统一的分布式信度结构形式。在实际情形中,为了方便原始数据的收集,往往单独为基础属性定义一组评价等级,因此存在基本属性与广义属性评价集不完全一致的情况,需要对基本属性分布评价进行等价变换。本文采用文献[18]方法对单值、区间值、语言变量等属性类型进行转化。
步骤2 计算属性权重。
当属性权重信息完全未知时,基于信度框架下三角模糊熵和熵权法的基本思想计算属性权重,计算方法如下:

(15)
当属性权重信息部分已知时,定义加权模糊熵,建立线性规划模型求解属性权重,计算方法如下:
E(S(ei(ai)))=
(16)
模糊熵值越小,即属性评价信息的模糊程度越小,从而决策确定性信息量越多,即方案越优。由此需要综合所有候选方案的模糊熵,令期望模糊熵取最小值,建立如下线性规划模型:
(17)

步骤3 对方案进行证据融合,得到广义分布评价。
使用证据推理信息融合算法,即利用式(1)~(12)可计算备选方案的广义分布评价。
步骤4 计算方案效用值,根据方案平均效用值对方案进行排序,选择最满意方案。
在证据理论中,通常用以基本信度值βn为下界,以βn+βH为上界所构成的区间值描述命题获得的信度,即以[βn,βn+βH]作为方案ai在广义属性y下被评为等级Hn的信任区间。明显地,若方案为完全评价,则区间信度退化为单值βn。
根据区间信度可定义方案ai的效用值。假设各等级的效用排序为u(H1) (18) (19) (20) 对方案al和ak,若uavg(al) 某房地产经营项目考虑三个备选方案a1、a2、a3,根据项目开发方案的经济效益、风险程度、环境效益、社会效益四个基本属性对项目进行综合评价,选出最优投资方案。四个属性分别表示为E={e1,e2,e3,e4}。具体数值如表1所示。 表1 某房地产投资项目三个方案属性Tab. 1 Attributes of three schemes for some real estate investment project 步骤1 转化决策信息,构建信度决策矩阵。 参照文献[18]的等价规则及分布评价等价规则,针对基本属性分布评价与广义属性分布评价等级不一致的情况进行模糊转化。如表2所示,信息转化后的证据推理框架下信度决策矩阵记为Dg=(S(ei(al)))M×L。 表2 信度决策矩阵Tab. 2 Belief decision matrix 步骤2 计算属性权重。 首先根据第2章提出的模糊熵公式计算各属性模糊熵,计算结果如表3所示。 表3 属性模糊熵Tab. 3 Fuzzy entropies of attributes 当属性权重完全未知时,根据式(15)可确定最优属性权重向量为w*=(0.141 1,0.453 9,0.210 2,0.194 8)。 当属性权重信息部分已知时,假设决策者给出不完全确定的属性权重信息为0.2≤w1≤0.4,0.12≤w2≤0.3, 0.1≤w3≤0.25,0.1≤w4≤0.25。参照式(16)定义加权模糊熵,根据式(17)可建立如下线性模型: minE(DM×L)=2.378w1+w2+2.073w3+2.142w4 s.t 0.25≤w1≤0.4 0.12≤w2≤0.3 0.1≤w3≤0.25 0.1≤w4≤0.25 w1+w2+w3+w4=1 通过求解上述线性规划模型,可以得到最优属性权重为: w*=(0.25,0.3,0.25,0.2) 步骤3 对方案进行证据融合,得到广义分布评价。 当属性权重完全未知时,可得广义分布评价为: S(y(a1))={(H1,0.578 4),(H2,0.113 4), (H3,0.114 1),(H4,0.147 1), (H5,0.047 0)} S(y(a2))={(H1,0.121 3),(H2,0.150 8), (H3,0.476 4),(H4,0.251 4)} S(y(a3))={(H3,0.067 9),(H4,0.235 9), (H5,0.696 2)} 当属性权重部分信息已知时,广义分布评价结果为: S(y(a1))={(H1,0.353 2),(H2,0.156 0), (H3,0.149 8),(H4,0.235 4), (H5,0.105 7)} S(y(a2))={(H1,0.165 6),(H2,0.253 0), (H3,0.438 7),(H4,0.146 2)} S(y(a3))={(H3,0.122 7),(H4,0.375 8), (H5,0.501 5)} 步骤4 计算方案效用值,根据方案平均效用值对方案进行排序,选择最满意方案。 首先定义广义评价集各等级效用值为u(H1)=0,u(H2)=0.25,u(H3)=0.5,u(H4)=0.75,u(H5)=1,在属性权重完全未知的情况下,各方案效用值为: umax(a1)=umin(a1)=uave(a1)=0.242 8 umax(a2)=umin(a2)=uave(a2)=0.464 5 umax(a3)=umin(a3)=uave(a3)=0.907 1 根据平均效用值的方案排序结果为a1a2a3,即a3为最佳投资方案。 在属性权重部分信息已知的情况下,各方案效用值为: umax(a1)=umin(a1)=uave(a1)=0.396 1 umax(a2)=umin(a2)=uave(a2)=0.389 6 umax(a3)=umin(a3)=uave(a3)=0.844 7 根据平均效用值的方案排序结果为a2a1a3,即a3为最佳投资方案。 首先利用文献[19]中提出的证据信息熵公式计算本文案例的权重结果,求得本文案例各方案属性证据信息熵如表4所示。 表4 属性证据信息熵Tab. 4 Evidence information entropies of attributes 文献[19]只提出了属性权重信息部分已知情况下的线性规划求解方法,因此进一步计算得权重完全未知情况下的权重为w=(0.25,0.3,0.2,0.25)。证据融合后的广义分布评价结果为: S(y(a1))={(H1,0.340 6),(H2,0.121 3), (H3,0.159 1),(H4,0.273 6), (H5,0.105 4)} S(y(a2))={(H1,0.141 6),(H2,0.238 8), (H3,0.478 5),(H4,0.141 1)} S(y(a3))={(H3,0.115 7),(H4,0.352 6), (H5,0.531 7)} 各方案效用值为: umax(a1)=umin(a1)=uave(a1)=0.420 5 umax(a2)=umin(a2)=uave(a2)=0.404 8 umax(a3)=umin(a3)=uave(a3)=0.854 0 根据平均效用值的方案排序结果为a2a1a3,即a3为最佳投资方案。 该方法与本文属性权重部分信息已知情况下的排序结果相同,验证了本文方法的有效性。但文献[19]中的证据信息熵权重法只适用于属性权重信息部分已知的情况,本文方法能够同时处理属性权重信息部分已知和属性权重信息完全未知的两种情况,适用范围更广。利用本文改进模糊熵公式确定权重时不仅考虑了信度决策矩阵的信任偏差度,且考虑了因无知而引起的不确定指数,能最大限度地保留原始信息,因此本文方法更具优越性。另外,再结合传统熵权法[18]与主观权重法[20]的排序结果进行比较分析,结果如表5所示。 表5 不同赋权法的结果比较Tab. 5 Comparative analysis of different weight methods 比较分析表5中五种不同赋权法产生的决策排序结果可知:首先,五种方法中的最佳方案均为a3,表明了本文方法的可行性和有效性。其次,当权重信息部分已知时,本文方法整体排序结果与文献[20]中采用主观估计法直接获得权重的结果一致;当权重信息完全未知时,本文方法排序结果与文献[18]中的采用传统熵权法的权重获取方法结果一致。当获取权重考虑主观因素时,次选方案为a1,属性权重完全未知时,次选方案则为a2。两种不同情况下排序结果的差异说明,当带有主观因素时,决策者可能更倾向于考虑投资方案的经济效益和风险程度,而忽视投资对象的环境效益和社会效益,因此造成了主客观情况下次选排序结果不一致的情况,这也说明了主、客观方法对决策结果有着重要影响。 本文方法通过定义基于三角函数的模糊熵客观地确定属性权重,减少了决策者在决策过程中的主观随意性;同时,本文方法不仅能够处理属性权重完全未知的情况,还适用于在属性权重信息部分已知的情况,更符合实际决策过程的需要。 为解决证据推理方法应用中属性权重难以获取的问题,本文提出一种基于改进模糊熵和证据推理的不确定多属性决策方法,给出了具体计算步骤和算例分析。所构造的基于三角函数的改进模糊熵公式不仅体现了证据推理信度决策矩阵内部的信任度偏差,且包含了因无知而引起的不确定性对决策的影响,从而能够更充分地反映决策信息的差异性、不确定性及未知性程度,避免了有效决策信息的丢失,更具优越性。更进一步,该方法可同时处理属性权重信息部分已知和属性权重信息完全未知两种情况,更具一般性。实例表明,该方法能够很好地适应不确定环境下的基于证据推理方法的多属性决策问题,客观性较强,能够运用到投资方案选择、供应商评估等实际管理问题中。4 实例分析
4.1 问题描述
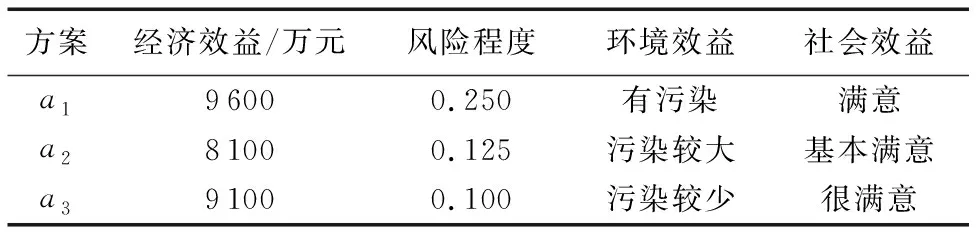
4.2 决策过程


4.3 比较分析


5 结语
——基于体育核心期刊论文(2010—2018年)的系统分析

