基于多目标遗传算法的云数据安全存储方法
吴 超,何利文,唐澄澄,侯小宇,周 睿
(南京邮电大学,江苏 南京 210003)
1 概 述
随着物联网的出现,数据的获取方式变得多样化,只要是接入网络的事物,通过传感器、控制器等硬件就能收集人类或者接入网络的任意事物的定位数据、反馈数据、个性数据等[1]。IDC Digital Universe study在2011年指出,未来全世界的数据每两年增加一倍,2020年的数据总量将达到当前的50倍[2]。由于物联网技术诸如无人驾驶、智能交通、虚拟现实对于网络质量的要求相当苛刻,目前还处于相对不成熟的时期。未来随着5G网络的商用普及之后,5G网络的高速度、低功耗、低时延、多互联等特点将支撑物联网进入井喷式的发展[3]。届时,物联网所获取的巨量数据将会给数据存储带来巨大的压力。目前来说,云存储系统是最成熟的大数据存储模型。
云存储将大量不同类型的存储设备通过软件集合起来协同工作,共同对外提供数据存储服务。云存储服务对传统存储技术在数据安全性、可靠性、易管理性等方面提出了新的挑战[4]。云存储的一个核心问题就是数据放置。对用户来说,云存储检索速度以及对于隐私数据的保护是评判云存储系统质量的两个重要因素[5]。旨在以最小的时间和空间代价为目的,文中提出一种数据放置方法来解决检索速度和数据安全问题。在云存储中,分布式的存储方式需要考虑到网络拓扑中一些实际问题,例如不同节点的不同容量、节点间的宽带、链路的长短等,因此数据放置问题需要考虑大量的参数去得到一个最优的数据放置方法。
当前,对于信息安全的研究主要集中在应对网络层攻击和对数据本身进行安全性处理两个方面[6]。对于数据放置安全性能的研究主要集中在数据加密技术。Liu J K等在对云存储系统的数据安全保护机制[7]的研究中提出了一种方法,即服务端仅提供加密数据而无法解密数据,用户则需要两个媒介才能解密文件,一个是解密密钥,另外一个是连接电脑的个人安全设备,只有同时具有两项才能解密。余琦等[8]在基于HDFS分布式存储的安全技术研究中提出了一种复合型加密方法,首先对存入HDFS的文件进行AES加密,然后再用RSA算法保障AES密钥安全。而一些云存储供应商比如Amazon S3和Google Cloud Platform提供了服务器端加密服务[9],根据安全级别用不同长度的密钥加密用户数据。薛矛等[10]在云存储系统之上添加一层安全系统架构Corslet,应用安全证书来提供端到端的数据私密性保护、完整性保护以及访问权限控制等功能。综上,对于加密算法或者安全架构的应用无疑在数据检索方面增加了计算的步骤,从而加大了时间开销。
而对于云存储系统的检索优化也进行了大量研究。袁野等[11]在其云环境下的虚拟机放置策略中,采取WFPSO算法优化节点部署策略,解决了复杂网络拓扑中的网络通信时延问题。Boru D等[12]在云系统数据中心复制算法的节能优化研究中,着力解决了云系统能耗问题,从而降低了I/O带宽负荷以及计算中的延迟。而在Su M等[13]的研究中,提出了一种北斗七星模型,将数据放置问题定义为一个最优化的非线性规划模型,在这一模型中,以量化的因素建立了不等式约束的目标函数,测量抽象空间的欧几里得距离,从而得到最优化的检索结果。然而,以上研究均未考虑云系统的安全性问题。
对于数据安全和检索优化的研究也相对成熟。黄永峰等[14]在云存储加密及其检索技术中提出了基于全同态加密的检索方法,采用信息检索中的向量空间模型,计算检索出的文档与待查询信息之间的相关度,对检索词词频和倒排文档频率进行统计,然后采用全同态方法对文档进行加密并建立索引方法,检索后将加密文档与索引项密文一起上传到服务器端。在Tu M等[15]提出的安全数据的最优化放置方法中,也解决了优化检索和数据安全的问题。但以上研究仍然采用加密的方式保护数据,从而存在额外的开销。Kang S等[16]在IEEE网络会议中提出了一种全新的云存储数据放置策略。在不使用加密的方式保护数据的前提下优化了检索速度。其思想是将隐私文件拆分为多个存储,而不同的数据块存放在不同的节点中,并且这些节点不会直接连接,保证在某一节点被入侵的情况下不会得到整个文件的有效信息,并且攻击者无法猜出剩下的数据块在哪一位置。其实现是将数据放置问题作为一个最小化检索时间的线性规划模型,并由节点的容量、节点间的带宽以及节点间的距离作为约束条件,以达到在保证数据安全的同时得到一个检索最优解。但其在算法上由两步构成,先用T-coloring算法选出符合安全需求的节点集,再对最短路径求解。这一方法在较复杂的网络拓扑中效率较低。
文中提出的方法在不使用数据加密的前提下解决了数据的安全需求和检索效率问题。并且在仿真试验中与传统的数据放置方法进行了对比。
2 云存储安全放置方法
2.1 系统模型
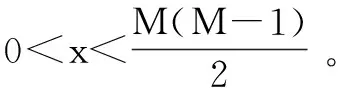
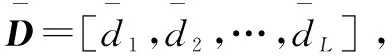
由于该模型中数据是采用分布式的方式将原始数据切分为多个数据块存放在不同的数据节点中,当系统的某个或者某些数据节点被恶意攻击以后,黑客无法猜出整体数据中所有的敏感信息。因此,对于恶意攻击者而言,单个数据节点的敏感信息是没有具体意义的,除非绝大部分包含有敏感信息的数据块被存放在了链路关系比较密切的几个数据节点当中。例如,数据节点被存放在了相邻的数据节点当中,黑客可以很容易地通过逐项遍历的方式检索到其他的敏感信息。另一方面,如果为了保证数据的安全性,将切分后的数据块放置得过于偏远,会增加用户正常的数据检索时间。文中要解决的问题便是在保证即使在某个单一数据节点被黑客攻击的前提下,也无法猜测出其他数据节点的具体位置。并且在此基础上需要满足最小化数据的检索时间。
保障数据存放安全的前提下最小化数据检索时间,首先是要保障所存储数据的安全性。因此,引入一种分布式相关性来定义系统的安全水平。具体为当原始数据被切分成多个数据块放置在不同的数据节点后,各存放有数据块的数据节点中可能会包含原始数据中的部分敏感信息。此时,存放在各数据节点中的数据块之间可能存在有相关度比较高的特征。
可以根据数据节点中数据含有的特征信息来描述相关数据节点之间的相关性。文中定义两个数据节点Si和Sj之间的相关性为其Pearson相关系数[17]:
(1)
其中,cov(DiDj)表示数据节点Si和Sj中存放的数据块Di和Dj的协方差。
根据概率论的相关理论可以得到[18]:
ρij=
(2)
其中,E[X]表示数据序列X的期望;0≤|ρij|≤1。当ρij>0时,表示数据块Di和Dj正相关,当ρij<0时,表示数据块Di和Dj负相关,并且|ρij|的值越接近于1时,数据块Di和Dj之间的相关性越大,|ρij|的值越接近于0,数据块Di和Dj之间的相关性越小。从数据存储的角度来说,为保证数据存储的安全,当数据块Di和Dj之间的相关性越大时,如果两个数据块存放在了两个逻辑距离比较近的数据节点中,若其中一个数据节点被恶意攻击后,黑客获取另外一个数据节点中的数据块信息的概率将会大大增加。因此,在这种情况下,设计数据的放置策略时应该尽量考虑将两个相关性较高的数据块存放在逻辑距离较远的两个数据节点当中。由此,可以定义系统中数据节点Si和Sj之间的安全水平为:
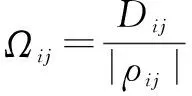
(3)
其中,Dij为数据节点Si和Sj之间的欧氏距离。
(4)
当数据节点Si和Sj之间不存在数据链路时,定义Dij=+。另外,式3表明系统的安全水平与数据块之间的相关性成反比,与数据节点之间的逻辑距离成正比。Ωij的值越大,表明数据的存放越安全。
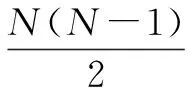
(5)
2.2 约束多目标优化模型
假设用户从数据节点Si发出数据查询请求,存储在数据节点Sj处的数据块Dn将会按照指令要求传输到数据节点Si中。则需要解决的一个基本问题是将数据块Dn从数据节点Sj传输到数据节点Si中的时间最小化。一个基本思路是找到数据节点Si和Sj之间的最短路径。文中定义数据节点Si和Sj之间的最短路径为Pij,则将数据块Dn在数据节点Si和Sj之间的最短传输时间定义为:
(6)
其中,e表示路径Pij上相邻数据节点之间的一段链路,e∈Pij;Bexy表示链路exy上的带宽;链路exy上的两个端点分别为网络的顶点vx和vy,即数据节点Sx和Sy。
文中要解决的根本问题是在保障存储数据安全的前提下最小化用户对数据的检索时间。实际上,该问题是一个多目标优化问题(multi-objective optimization problem,MOP),包括最小化数据的检索时间T和最大化系统的安全水平Ω。因此,结合式5和式6,可以得到最小化检索时间的目标函数为:
(7)
文中系统设计的目标是在保证系统数据安全的前提下最小化数据的最小时间,即:
Minimize:F(S)
(8)
Subject to
(9)
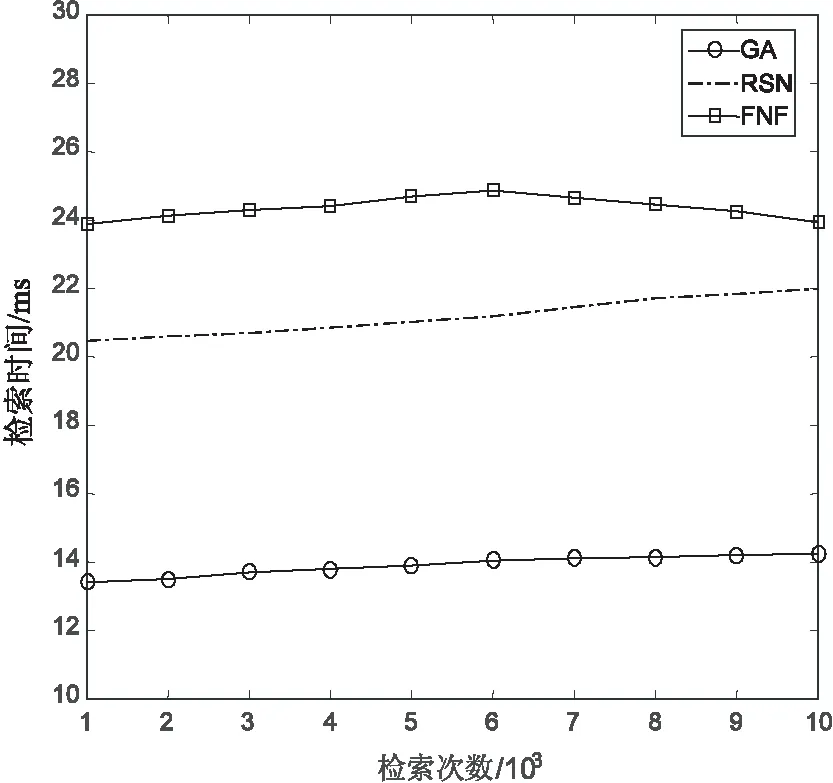
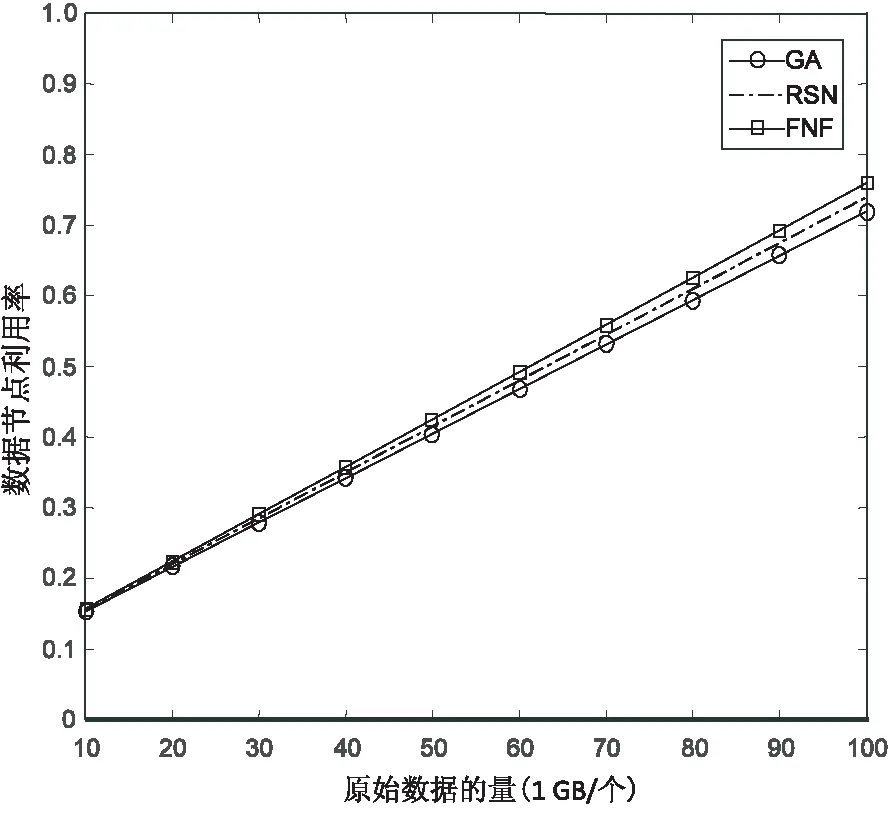
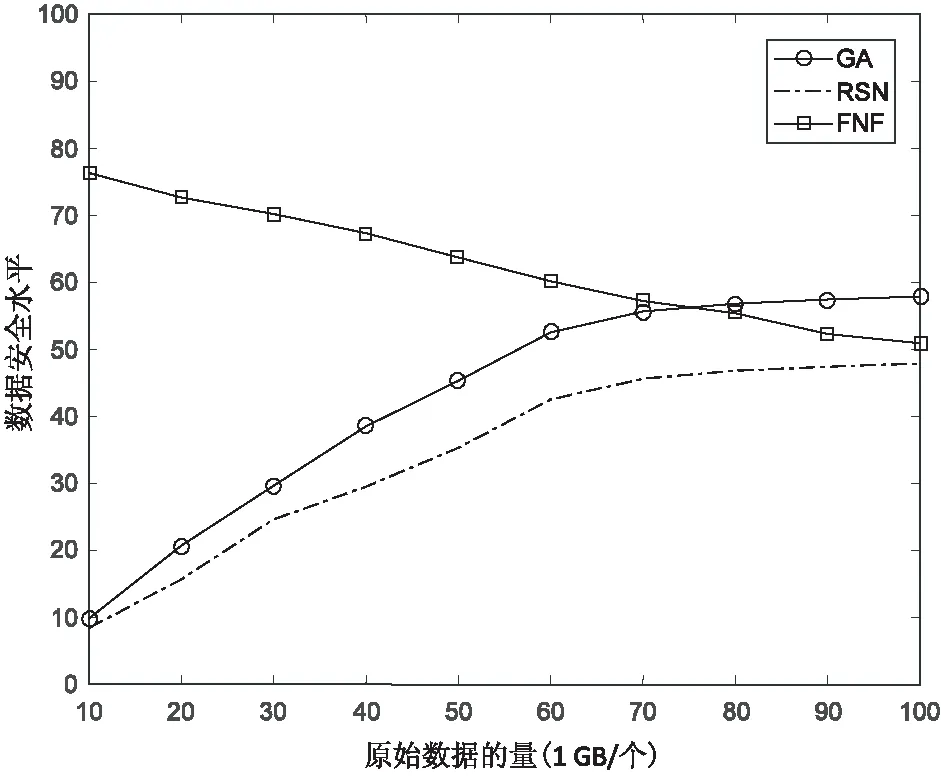
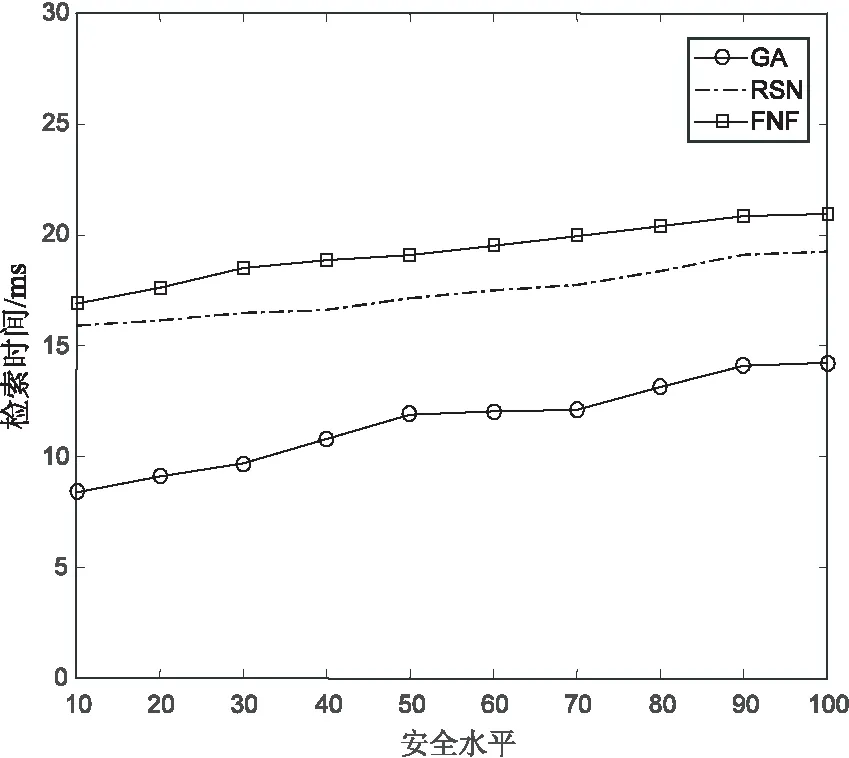
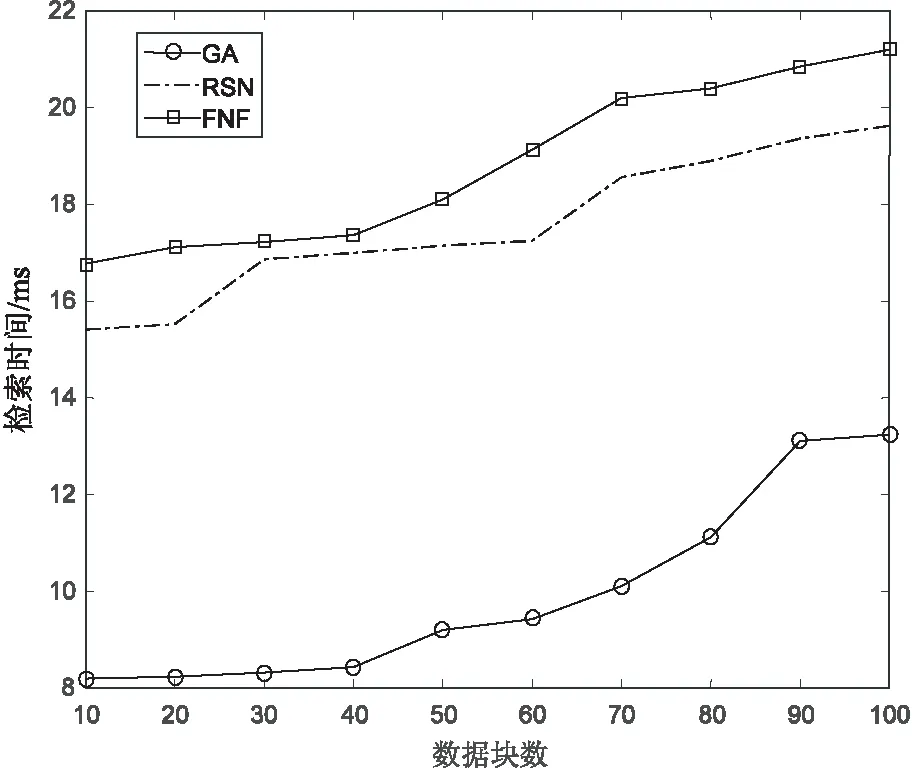
0 (10) 式9表示所有数据块的尺寸总和是等于原始数据的尺寸的;式10表示存放在数据节点Sn处数据块的尺寸是小于数据节点Sn的最大容量Cn的。 通过以上最优化模型在一个分布式的存储系统中获取最优化的数据放置策略是一个NP难题,传统的数值计算方法往往不能有效计算其全局最优解。对于此类问题,采取约束优化问题的方法进行求解。约束优化问题(constrained optimization problems,COPs)是指在一系列参数的约束条件下,针对问题求出最优化目标的问题。目前,求解该问题的算法大致有两类:确定性算法和不确定性算法。前者包括投影梯度法、填充函数法、惩罚函数法、序列二次规划法等,这些方法的求解大多依赖函数的初始值以及梯度信息,对于最优解的收敛较慢,易陷入局部最优解,且对于连通性差,不可导以及没有函数表达式的问题没有很好的解决方法。后者不依赖问题本身的严格数学性质,在解决全局最优解的问题中比较有优势。运行时间相对较短且描述简单,容易实现。不确定算法主要是一些启发式算法,包括模拟退火法、蚁群算法、遗传算法等。文中将重点研究遗传算法。 2.3.1 遗传算法 早在20世纪40年代,就有学者开始模拟生物活动研究计算机技术。其中部分学者提出了类似生物进化规律的随机搜索算法。Holland教授于1975年在其著作《自然系统和人工系统的自适应》中正式定义了遗传算法。遗传算法是基于达尔文进化论的启发以模拟生物界物种进化而形成的启发式算法,其目的是求取全局最优解,具有随机性的特征。其不依赖梯度信息的特点被广泛应用于无约束优化问题,一旦初始参数确定后,遗传算法将以与问题本身无关的方式进行求解。在不断的优化过程中使其同样可以处理约束优化问题。 遗传算法的基本思想是模仿一个种群的繁殖行为,由父代的染色体通过交叉、变异得到后代的过程。在该过程中根据达尔文的进化理论淘汰掉比较差的后代(不符合线性收敛的个体),存活下来的个体不仅继承了父代的优点,并且更加适应环境、更加优秀。子代中优秀的个体再不断繁殖进化。每一次迭代都能够得到比前一代更好的个体。并最终实现了全局最优解。 遗传算法的核心操作是选择、交叉和变异。其过程是将解转换为可以进行交叉变异的染色体结构,给定满足约束条件的初始解进行繁殖操作,并遵循适者生存、优胜劣汰的自然选择法则剔除相对较差的后代,保存比父代更好的近似解。进行多次迭代直到产生满足条件的最优解时终止算法。其具体步骤如下: (1)编码:每个问题的解都看作是一个可以进行交配的染色体,所以先将问题的解转化为染色体结构。染色体上的DNA可以进行自由组合。 (7)迭代:判断种群是否达到阈值φ,如不达到继续执行步骤5、6,如达到则中止迭代并得到最优解。 整个遗传算法流程中先后需要确定遗传算法的参数选取、编码方案、适应度函数、算法终止准则(确定阈值)、遗传算子的设计(包括选择算子、交叉算子以及变异算子)。并且还要考虑算法能够支持并行运算,以确保算法的运行效率。 2.3.2 基于多目标遗传算法的云数据安全放置算法 首先将式7~10中的最优化问题转化为标准化的遗传算法求解问题: Maximization:-F(S) (11) subject to: (12) 0 (13) 式12中,δ为等式约束条件的容忍值,一般取一个较小的正值。将式8中的等式约束条件转换为不等式约束条件后,式8中的等式约束将转化成一个不等式约束问题。 针对最小化检索时间问题的特点,构建了该问题的遗传算法。 (1)编码方法的确定。 由于文中设计的系统数据是被切分为N个长短不一的数据块分别存放在不同的数据节点中,因此采用自然数编码的方式对所要求解的问题进行编码。用0表示数据的查询节点,用1,2,…,M-1分别表示其他的各数据节点。这里的数据节点可能存有数据块,也可能没有存储数据块。当Sm=0时,表明数据节点m中没有存储数据块;当Sm≠0时,表明数据节点m中存储有数据块。由于原始数据是被切分成长度不一的N份存放在N个数据节点中,则网络中将会存在N-1条数据传输路径,以便将各数据节点中存储的数据块传输到查询节点0处。数据在传输路径上进行传输,必然经过路径上的多个数据节点,也有可能不经过某些数据节点。由此可知,还剩下M-N+1个数据节点没有存储数据块信息。为了在编码中反映这N-1条数据传输路径,设定1,2,…,M-N+1个互不重复的自然数随机排列构成一个个体,对应一种数据放置策略。例如,数据节点的个数为10,数据块的个数为5(假定其中有一个数据块0存放在数据节点0处,数据节点0处为用户查询节点),则可以用1,2,…,9(其中5,6,7,8,9这几个数表示没有存放数据块)这9个数随机排列,将其存放到9个数据节点中。如个体1,2,4,7,3,6,8,5,9表示数据块存放在数据节点0,1,2,4,7这5个数据节点当中。 (2)初始群体的确定。 随机产生一种1~M-1这M-1个互不重复的自然数排列,即形成一个个体。设群体的规模为N,则通过随机产生N个这样的个体,形成初始群体。 (3)适应度评估。 对某个个体所对应的数据放置方案的优劣进行判定,一是要看其是否满足网络系统的约束条件,而且要计算其代价函数值。根据基于数据安全约束最小化检索时间的特征要求所确定的编码方法,隐含了存放在各数据节点中数据的尺寸之和等于原始数据的尺寸,并且各数据节点中所存储的数据块的尺寸一定是小于该数据节点的容量的信息。另外,存放数据块的数据节点之间一定满足式3的要求。因此,在设计数据的放置策略时需要同时考虑这几个约束条件,若不满足则判定该方案不可行,最后计算其代价函数值。对于某个个体k,设其对应的数据放置方案的不可行个数为φk,其代价函数值为Zk,则该个体的适应度Fk表示为: (14) 其中,w对每个不可行放置策略的惩罚权重,可以根据代价函数(式11)的取值范围取一个相对较大的数值。 (4)选择操作。 (5)交叉操作。 除排在第一位的最优个体外,对另外N-1个新产生的个体按照概率pi进行交叉重组。 (6)变异操作。 在选择机制中,采用了保留最优个体的方式。为保障群体内个体的多样性,采用连续多次变换的变异技术。变异的概率为pj,一旦发生变异,则变异交换的次数通过随机的方式产生。 文中通过计算机实验仿真来验证提出的基于多目标遗传算法的云数据安全放置方法。 假设整个云存储系统中的M个数据节点S是一个随机的拓扑网络,并且每一个数据节点在网络系统中都具有一个固定的位置坐标Sm,其位置坐标具体为其在网络中的MAC地址。数据节点的存储容量随机设定为(256,1 024)GB;需要存储的原始数据的尺寸设定为(0.5,2)GB;网络中数据节点之间的带宽随机设定在(100,500)MB之间,并由此构成网络链路的带宽矩阵B。 为了对基于多目标遗传算法的云数据安全放置方法的可用性和有效性进行系统化的评估,利用检索时间、数据节点的利用率、安全水平三个评估标准来对其进行衡量,具体为: (1)检索时间:基于多次查询,对于检索操作的实际检索时间(所有数据块传输到查询节点的时间)求平均值。 (2)数据节点利用率:数据放置策略中存在对于N个数据块的选取。在多个文件存入时,查看M个数据节点中实际被使用的节点占比(最小为N/M)。 (3)安全水平:根据文中安全水平的定义,计算出当前数据块间的安全水平。 为对比分析实验的结果,参考文献[16]中的方法对数据节点的选择策略进行了设计,该策略用以从M个数据节点中选出符合整体安全水平的N个节点存入N个数据块。其思想是设定一个节点集,初始包括随机选择的一个数据节点,根据不同的选择策略选出一个节点插入当前节点集并确保节点集中两两节点间的安全水平不低于最小安全阈值,且平均安全水平不低于平均安全阈值。以下为2种节点选择策略:随机选取节点(random selection of nodes,RSN),按照节点选择策略随机选择包含N个节点的节点集;最远节点优先(furthest node first,FNF),选择离当前节点集中节点平均距离最远的并且符合节点选择策略的包含N个节点的节点集。 实验首先需要对遗传算法中所涉及的编码、选择、交叉、变异等操作过程进行设计,其具体设计方法可以参见文中的算法描述。 仿真实验1验证、比较了提出的基于多目标遗传算法的云数据安全放置方法中数据检索次数和原始数据量对数据检索时间、数据节点利用率以及安全水平的影响程度。其中原始数据被切分为数据块的数量为30。图1中设定数据节点数为100。从图1的结果可见,文中算法的平均检索时间小于其他算法。 图1 检索次数的影响 图2描述了随着存储原始数据量的增加,数据节点的利用率的变化情况。图中数据节点的数量设定为200。可以看出,随着原始数据量的增加,数据节点的利用率显著提高,表现为数据的分散程度比较高,即原始数据切分后的数据块是分散存储在存储系统中的,验证了系统的安全性。 图2 数据量与节点利用率的关系 图3描述了随着存储原始数据量的增加,数据安全性的变化情况。图中数据节点设定为200。如图所示,随着原始数据量的增加,GA算法和RSN算法的安全水平也有相应提高,这是因为当原始数据量较少时,算法倾向于选择离检索点相对比较近的节点,随着原始数据量的增加,数据块需要存储在距离较远的数据节点中。这与式3中提出的安全水平理论一致。而FNF由于是选择最远节点,故开始时安全性能最高,但后期呈下降趋势。 图3 数据量与安全水平的关系 仿真实验2验证、比较了在不同的安全水平、数据节点数、数据块数量下,检索时间的变化情况。图4中设定数据节点数为100,数据块数为30。结果显示,随着安全性能要求的提高,各算法的检索时间均有所增加,这是由于安全性能的提高直接增大了数据块之间的距离,所以检索路径长度增加。 图4 安全水平的影响 图5 节点数的影响 图5中设定数据块为30,结果显示,随着数据节点数的增加,检索时间呈现增加的态势,这是由于在更大的网络拓扑下,数据块的物理距离的增大所引起。 图6中,原始数据的尺寸大小设定为2 GB,该原始数据被切分为不同数据量的数据块,比较分析其数据检索时间的大小。数据节点的个数设定为200。结果显示,随着数据块数量的增加,检索时间增加。这是由于在N条检索路径上传输的总数据不变,N的增加必然会增加检索路径的长度。 图6 数据块数的影响 该节通过多次仿真实验,将不同的参数设为变参,均显示出GA算法在检索时间开销上优于FNF和RSN算法。同时在安全性能方面,FNF和RSN算法均优于GA算法,这是由遗传算法自身特性所决定的,GA算法中的安全性能与安全阈值紧密相关。并没有对安全水平进行最优化,但可以通过调整阈值,定义GA算法的整体安全性能,已达到实际中所需要的安全需求。 为解决当前云存储系统的两个核心问题即数据安全和检索效率,提出了基于多目标遗传算法的数据安全放置方法。该方法以数据安全性和检索效率为目标,建立了多目标优化模型,采用遗传算法来解决问题。并且在随机网络拓扑环境中进行了仿真实验以验证其效率。仿真结果表明,该算法在保证数据安全的前提下,优化了检索效率。同时鉴于遗传算法具有较低的时间复杂度,在该算法中抛弃了传统的加密模式,能够保证较高的运算效率。2.3 多目标遗传算法
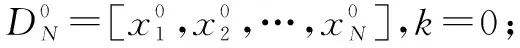
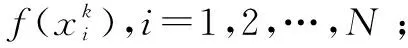
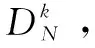
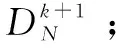
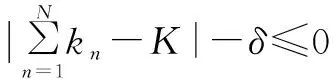
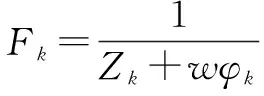
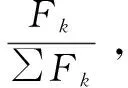
3 实验仿真与分析

4 结束语

