基于Hadoop平台的改进KNN分类算法并行化处理
马 莹, 赵 辉, 崔 岩
(长春工业大学 计算机科学与工程学院, 吉林 长春 130012)
0 引 言
随着科技的快速发展和大数据时代的到来,各领域的社交媒体都在时刻产生大量的数据,而这些数据都存在着潜在的价值[1]。当前,数据挖掘作为发现数据库中有价值数据的关键技术,引起了广大学者的高度关注[2]。数据挖掘是指从庞大的数据量中发现隐藏在其中有价值的数据信息的过程,在市场分析、信息统计、科学探索等方面都得到了广泛应用。常用的传统分类算法有:支持向量机(Support Vector Machine, SVM)、K-最近邻(K-Nearest Neighbors, KNN)、朴素贝叶斯(Naive Bayes, NB)等。其中KNN分类算法有着思想简单、理论成熟、易于实现、准确度高等优点,因此被广泛应用于各领域的数据挖掘中。但是传统的KNN分类算法也存在着以下缺点:
1)传统的KNN分类算法作为文本分类中被广泛应用的算法之一,在分类过程中,要计算每一个测试样本与训练样本集中每一个点相似度或距离,因此,在此过程中会由于计算量庞大而耗费大量的时间,最后导致分类速度减慢,算法的时间复杂度增高,分类效率降低。
2)如果训练样本集处于不均匀状态,那么最终会导致分类的结果不准确。然而,随着各领域的数据量不断增加,传统分类算法已经不能满足当前的数据分析需求,因此,提高算法的分类时间和分类准确性是当前数据分类至关重要的问题。
如今,已有很多研究者对KNN分类算法进行了相关的探究和分析。任朋启等[3]通过对训练样本集高密度的部分进行了剪裁,并对剪裁后的训练样本集进行了投影寻踪理论,提出了一种改进的KNN分类算法----IKNN分类算法,从而提高了分类的准确性。邓振云等[4]通过引入重构和局部保持投影技术,提出了基于局部相关性的KNN分类算法,从而提升了KNN分类算法的分类效率。涂敬伟等[5]通过将KNN分类算法与MapReduce框架相结合,提出了一种在MapReduce框架上实现KNN分类并行化计算的研究,研究结果表明,此方案有着良好的加速比和可扩充性。
传统的KNN分类算法存在着在分类过程中会耗费大量的时间去计算样本间相似度或距离的情况,为了解决此问题,文中首先使用K-medoids聚类算法对训练样本集进行了剪裁,去除了样本中相似度较低的部分;然后结合Hadoop平台中的MapReduce框架实现数据的并行化处理,使其在多个节点上进行运算,从而降低了算法的时间复杂度,提升了算法的运行速度。
1 Hadoop平台
Hadoop平台最核心的设计是HDFS(Hadoop Distributed File System)[6]和MapReduce[7]。HDFS是Hadoop的一个子项目,是数据分布式操作的基础,它是以流数据访问模式来存储超大文件,适合运行在通用硬件上[8],具有高可靠性、高可扩展性等特征。而MapReduce是Hadoop平台中一个并行计算的框架模型,为大量的数据提供并行化模式。它具有数据分类、计算工作调度、系统优化等主要功能[9]。MapReduce编程模型的计算过程分为两部分:Map函数和Reduce函数,用户只要实现Map函数和Reduce函数,就可以完成分布式计算[10]。具体分为以下几部分:
1)用户提交数据信息后,MapReduce首先读取HDFS中的数据信息,并将其分割成M个split,然后将划分的信息传送给JobTacker,并通过Fork创建master和worker。
2)在Map阶段,Map任务数量是由片段M决定的,与split是一一对应的,并且每个Map任务之间是相互独立的。
3)Map函数和Reduce函数都是以
4)在Reduce函数阶段,将获取的中间结果按照key值进行遍历排序,使得同一key值所对应的value值在一起。
5)将中间结果以
2 KNN算法描述
KNN分类算法是在1968年由Cover和Hart提出的,是数据挖掘中最简单的方法之一,在语言处理、图像分析、信息检索等方面都得到了广泛的研究和应用[11]。它的基本原理是:
首先对待测试样本集与训练样本集中的每一个点进行相似度或距离计算,然后找出与测试样本距离最近或是相似度最高的K个训练样本,并以此作为待测试样本的K个近邻,最后根据K个近邻所属的类别对待测试样本进行划分归类,找到最终属于哪一类别。
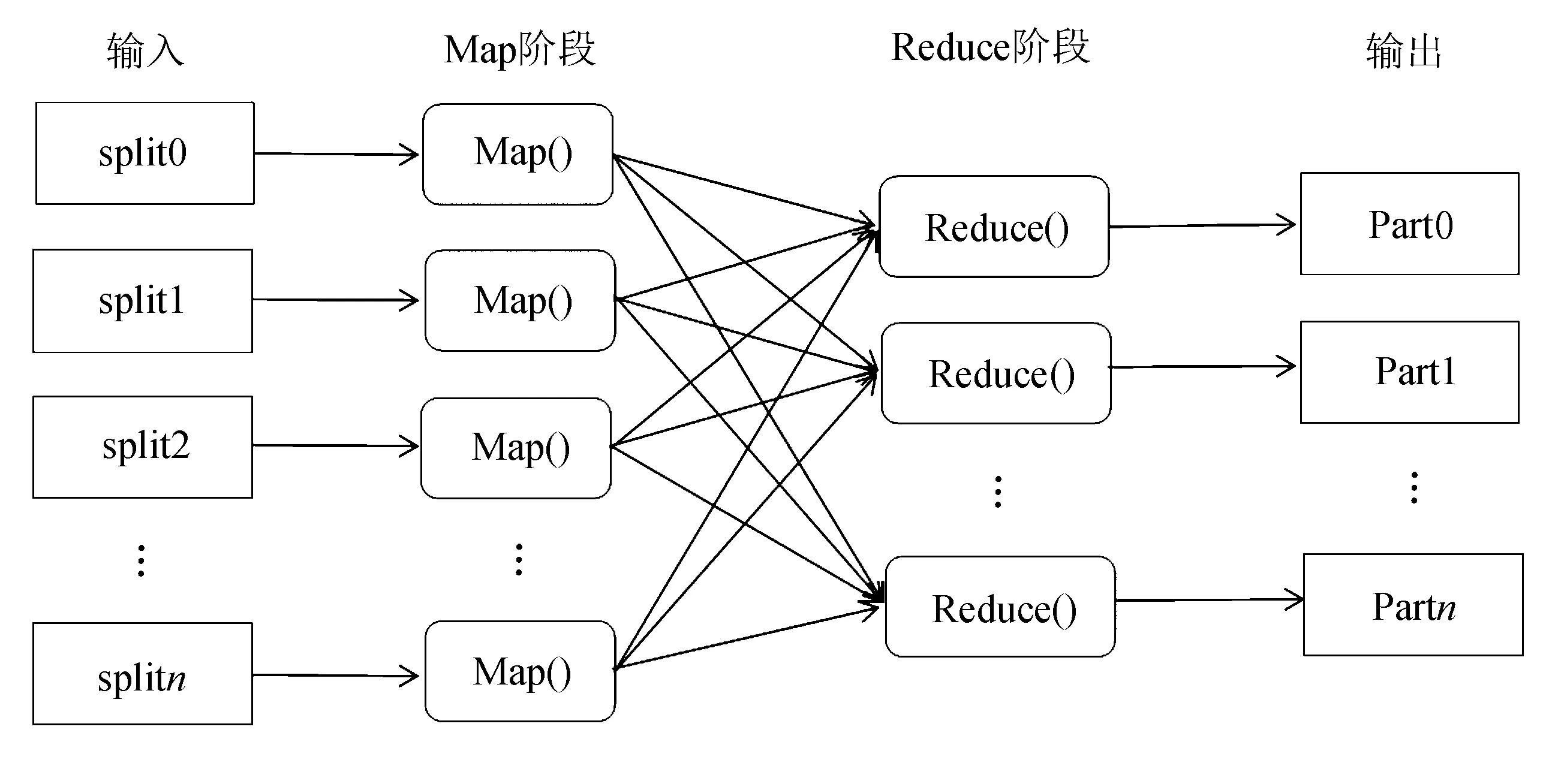
图1 MapReduce编程模型
KNN分类算法具体实现步骤:令D代表训练样本集,其中N代表D的样本类别个数,表示形式为{C1,C2,…,CN},M代表训练样本集数量,n代表特征向量的维度阈值,di代表D中的一个样本的特征向量,表示形式为{xi1,xi2,…,xij,…,xin}(0 (1) 计算出待分类样本与训练样本集中每一个点的相似度后,通过式(1)找到了待分类样本的相似度最高的K个最近邻样本,再通过下式计算出待分类样本归属于每一个类别的权重,最后将待分类样本按照权重大小进行划分,分配到权重最大的类别中。 (2) 其中,y(dj,Cj)为类别属性函数,如下式: (3) KNN分类算法虽然易于理解,计算简单,但是也存在着一定的缺点,文献[12]指出在分类过程中需要计算待测试样本与训练样本集所有点的距离,这样浪费了大量的分类时间,从而减少了KNN分类算法的分类效率。针对传统KNN分类算法在分类过程中存在计算量较大的问题,文中将K-medoids聚类算法引入到训练样本集中进行聚类剪裁,从而降低相似度的冗余计算。 K-中心聚类算法,即K-medoids聚类算法,是一种被广泛应用于数值统计、统计学、数据探索、医学诊断等重要领域的传统聚类方法,它具有数据简洁、计算简单、高健壮性等特性。 令训练样本集为D,其中D的样本类别数为N{C1,C2,…,CN},训练集中共包含的样本数为M,训练样本集剪裁方式如下: 1)K-medoids初始簇心的选择和优化。 ①对训练样本集D进行划分,将其分为m个簇,其中m=3*N。 ②为每一个簇随机选择一个点作为簇心Oi(0 ③计算出训练样本集D中所有点到簇心Oi的相似度,并按照相似程度对其进行分配。 ④在每一个簇内,首先令簇内的每一个点作为簇心,然后计算簇心到其他簇的相似距离和,最终选择相似距离和最小的簇心作为簇内新的簇心Oi。 2)对替换簇心搜索进行优化。 ①选择一个未被选取的簇心Oi替换簇心集A,从而不再使用全局的非簇心集,而是使用距离簇心Oi最近的j(j代表迭代次数,0 ②计算出在簇心集A中选取的没有被选择过的非簇心Qi与簇心Oi之间的平方误差之差,并将计算结果写在集合Q中,直至簇心集A中的所有非簇心都对比过。 ③如果集合Q最小值小于0,用集合Q中最小值所对应的非簇心替换原簇心,替换后得到新的簇心集合。然后把剩下的文本分给对应的簇内,其中此簇的簇心相似度最大。最后从步骤①重新开始进行计算。 ④如果集合Q的最小值大于或等于0,那么停止计算,最终取得m个聚类簇心。 3)训练样本集剪裁。 统计待分类样本与m个聚类簇心的相似度,如果Sim(D,Oi)小于Ti(其中,Ti代表第i个簇的簇内阈值,即簇内样本与簇心的最小相似度),表示待分类样本与簇内样本的相似程度比较低,因此可以把该簇内包含的样本进行剪裁,否则把该簇内包含的样本添加到新的训练样本集中。 KNN分类算法主要是获取k个最近邻,要实现这一过程必须通过大量的距离计算。设计并行计算可以明显地减少分类时间,提高分类效率。基于Hadoop改进的KNN分类算法实现MapReduce框架并行计算的基本思路是:首先将训练样本集分配给不同的节点进行Map函数操作计算形成键值对的形式,完成数据记录到训练样本距离的相似度计算以及相关的排序操作,相似度计算采用的是标准的欧式距离计算度量,结果存入到Context集合中,在此过程中每一个Map函数之间操作过程是没有关联的;然后将Map函数操作的计算结果作为中间结果是以 文中的Map函数和Reduce函数的相关伪代码如下: Map函数的伪代码: Input:Text key,Vector value Output: Begin: For i=0 to n (training dataset) do t=FindCatalog(i); For all k∈testfile do Distance=EuclideanDistance(k,ji); Context,write(key,vector(t,Distance)); End For End For End Reduce函数的伪代码: Input:Text key,Vector value Output:Text key,Vector value,Context context Begin: For all key and value do Array List(vcetor(t,value)); Sort(Array List); New ArrayList result; If k For i=0 to k do result.add(key,ArrayList.get(i)); Else System.out.println(“no sufficient training samples”); Context.write(key.Tradition KNN(result)) End for End for End 传统的KNN分类算法的时间复杂度为O(r1r2),r1为训练集样本数量,r2为测试集样本数量。文中对训练集数据进行了聚类剪裁,降低了相似度的冗余计算,从而生成新的训练集,数目为r3,此时时间复杂度为O(r2r3),在改进的KNN分类算法之上并结合MapReduce框架对KNN算法实现了并行化处理,时间复杂度为O(r2r3/n),n为节点个数。由于r1>r3,所以基于Hadoop平台改进的KNN分类算法的时间复杂度与传统的KNN分类算法的时间复杂度关系为O(r2r3/n) 实验平台为12台虚拟机构成的集群,CPU型号为Intel(R) Core(TM) i7-4790 CPU @ 3.60 GHz,内存为8 G,Hadoop版本为2.6.0。 文中采用微博文本作为实验数据进行分类,语料中分为正向情感和负向情感两个类别,每个类别中有5 000篇文本,共计10 000篇文本。根据需求从每个文本类别中随机抽取1 000篇文本,共计2 000篇文本作为训练集。为了实验的有效性和全面性,将剩余的数据分为不同规模的测试集,见表1。 表1 测试集 针对算法性能方面的评价指标,比较加速比、正确率P与运行时间t,其中加速比公式为: (4) 正确率公式为: (5) 实验1:在单一节点上,以正确率P与运行时间t作为评价指标,对传统的KNN分类算法、基于K-medoids改进的KNN分类算法二者之间进行了比较。比较结果如表2和图2所示。 表2 两种算法的比较 图2 两种算法的运行时间的比较 从表1和表2可以看出,测试样本集A1中的信息数据量比较少,文中基于K-medoids改进的KNN分类算法的正确率比传统的KNN分类算法降低了0.6个百分点,这是由于通过K-medoids聚类算法剪裁后的算法为近似算法,当数据信息量较少时,会对分类结果的正确率产生一定的影响;但是在时间方面上,由图2可以明显看出,基于K-medoids改进的KNN分类算法比传统的KNN分类算法缩短了13%~22%,而且随着数据量的增大,计算时间也缩短的越为明显,这是由于剪裁之后,降低了相似度的冗余计算。 实验2:加速比主要是用来权衡一个系统的可扩充性。在基于Hadoop平台改进的KNN分类算法下,针对节点个数不同时,对不同规模的测试样本集之间的加速比进行了比较,结果见表3。 表3 基于Hadoop平台的改进KNN分类算法 根据表3可以看出,基于Hadoop平台改进的KNN分类算法的加速比随着节点个数的增加而保持着线性上升,并在节点个数增加到30个时,加速比明显升高。多个节点可以明显缩减分类过程中所需要的时间,这表明在操作KNN分类算法时Hadoop平台上具有较好的加速比。由此可见,当节点个数逐渐增加时,加速比增长的速度也会更快。 文中主要研究基于Hadoop平台的改进KNN分类算法的并行化处理,首先通过K-medoids聚类算法对传统的KNN分类算法进行剪裁,然后通过Hadoop平台中的MapReduce框架实现数据并行化计算。从表1和表2中可以看出,在选择完整的测试集时,基于K-medoids改进的KNN分类算法比传统的KNN分类算法在运行时间上缩短了150 s;从表3可以看出,加速比随着节点个数的增加而快速增长,特别是节点个数在30~50之间的时候,产生以上原因是因为Hadoop平台的关键技术之一----MapReduce框架,在此框架上实现数据的并行化计算,提高了在分类过程中的运行时间。 在大数据时代通过对传统KNN分类算法的分析和研究,文中提出了基于Hadoop平台改进的KNN分类算法的并行化处理。首先将K-medoids聚类算法引入到传统的KNN分类算法中,对KNN分类进行剪裁,去除了相似程度较低的文本,然后运用Hadoop平台中的MapReduce框架对文本数据实现并行化计算,在分类过程中减少了算法的时间复杂度,提高了分类速度。实验结果表明,选择基于Hadoop平台的改进KNN分类算法对文本分类在时间复杂度方面取得了良好的分类效果,提高了分类效率,并且能够适用于当前的大数据环境。3 KNN分类算法的改进
4 改进KNN算法的并行化处理
4.1 基于Hadoop平台的改进KNN分类算法并行化处理
4.2 时间复杂度分析
5 实验结果与分析
5.1 实验环境与数据集

5.2 实验及结果
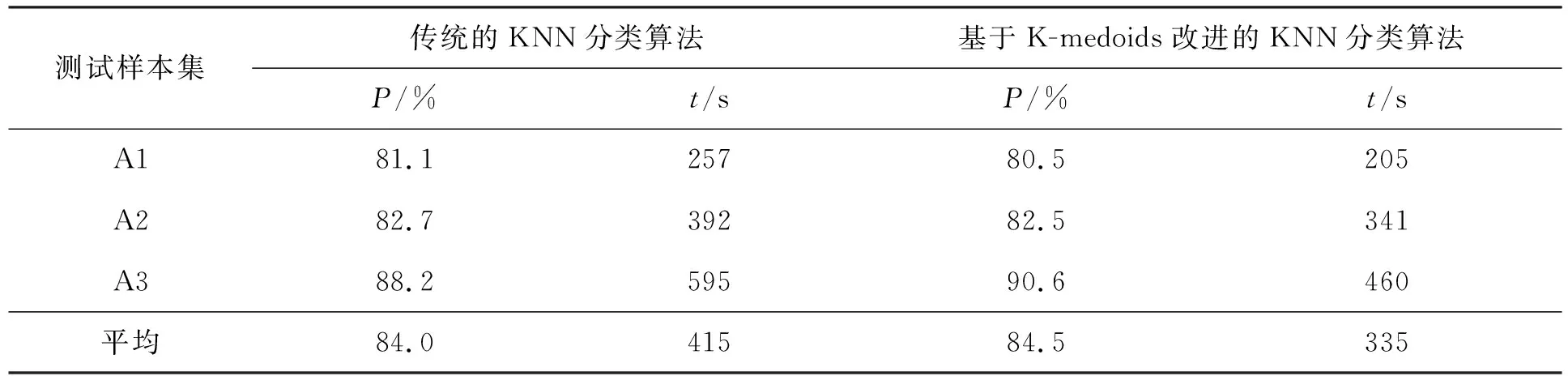

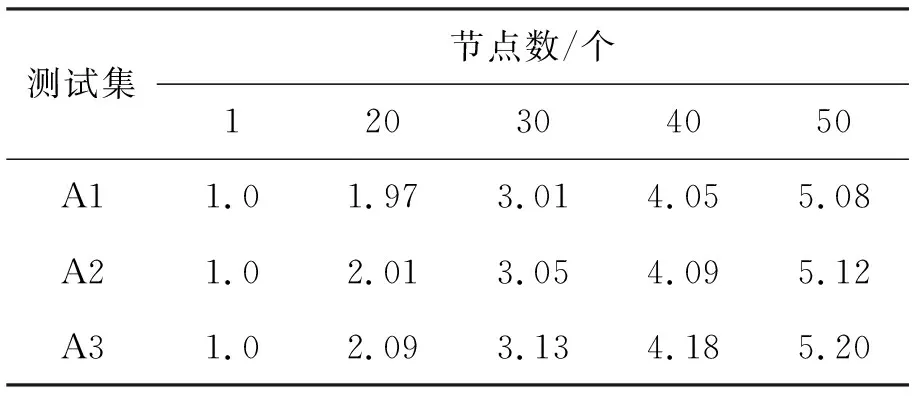
5.3 实验结果分析
6 结 语

