思维导图,“双结构”教学的神助攻
江苏省太仓市第一中学 李秀红
教学中,帮助学生掌握概括化、结构化的知识内容和方法程序,学生就能自主、独立地学习某一类知识,解决某一类问题。概括化、结构化的知识内容和方法程序就是学生主动学习的工具(简称“双结构”)。思维导图作为一种建构性知识整合,提高学习效率的新型高效的思维工具,在促进学生主动学习的初中数学“双结构”课堂教学中起到神助攻的作用。
一、思维导图在课前预习中的作用
概念课的预习:数学概念的学习和理解是学习数学的第一步,然而概念课学生往往不善于预习,或者预习仅仅是流于形式。对着教材草草看一遍,圈下黑体字,对基本概念不能形成知识网络,更不能够比较深刻地了解概念之间的联系。借助于思维导图,可以使学生进一步理解概念之间的联系,在头脑中形成条理化的认知结构。
例如《直线与圆的位置关系》第一课时,要求学生预习书本后完成思维导图。通过预习、整理思维导图,学生找到了点与圆的位置关系与直线与圆的位置关系的联系:从图形上观察或者从数量关系上来比较判断,从而真正起到了自主学习的作用。
复习课的预习:复习课是数学教学中的一个重要环节,具有容量大、时间紧、密度高的特点。单元复习或期末复习时,学生头脑中的知识比较杂乱,教师要及时引导学生借助于思维导图建立知识网络,及时查漏补缺,从而大大减轻学生负担,提高学习效率。
例如《一次函数》复习课,学生在认真制作思维导图的过程中,对一次函数进行了整体复习,理清了内容脉络。在此基础上完成前置作业:在平面直角坐标系中,A、B点坐标分别为(-2,0),(0,4),结合所学知识,你能设计哪些问题?
作为一道开放型问题,学生根据本章节知识点设计了一系列不同梯度的问题:
(1)线段AB长度,函数解析式,直线AB所在象限,增减性,该直线与坐标轴围成图形的面积。
(2)x轴上是否存在点C,使得△ABC为等腰三角形?
(3)点D与A、B、O围成平行四边形,求D点坐标。
(4)直线AB上到坐标轴距离为1的点坐标。
二、思维导图在课堂探究中的作用
在《一次函数复习(面积问题)》的课堂探究中设计了两个例题并配上相应的练习,研究面积问题的解题策略、思想方法。
已知解析式求面积符合学生,正向认知,学生处理起来比较顺利。在求四边形面积时方法很多:将四边形割成一个直角梯形和一个直角三角形;连接OM分割成两个三角形,还有将四边形看作两个三角形面积之差处理的等等,通过转化的方法求不规则图形的面积。
例2 已知一次函数的图像过点Q(-2,0),若该图像与y轴的交点为P,且△POQ面积为4。(1)求P点坐标。(2)求该一次函数解析式。
已知面积求解析式问题要求学生运用逆向思维,实际操作情况并不理想。主要原因是两方面:①学生不会规范地书写过程;②出现了漏解情况。由线段OP=4,很多学生只得到P(0,4),而没有考虑到P点在y轴负半轴的情况。关键环节在于由线段长转化到点坐标时没有考虑全面。
针对上述两个课堂探究的内容,引导学习小组合作完成本节课的思维导图:
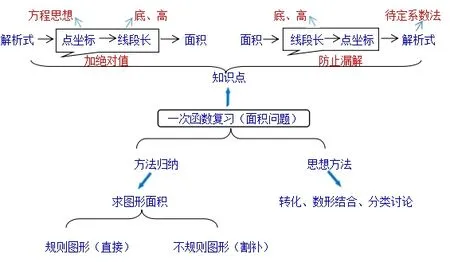
课堂上运用思维导图进行小组合作学习,可以在很大程度上改变传统合作学习流于表面的尴尬情况,真正起到优化课堂教学的作用。在课时总结环节,先让每个小组成员依据自己的水平与能力,运用思维导图进行知识点、解题策略、思想方法的总结,然后在组长的组织下有序讨论,组员分享各自的思维导图雏形,再借助于展示环节进行交流、对比、优化,制作出完整的思维导图,使合作学习真正落到实处。
三、思维导图在课后复习中的作用
课后复习是巩固知识,提高运用知识分析问题、解决问题能力的重要环节。借助于思维导图构建知识网络,除了按章节复习之外,还可以按照知识分类复习。如方程(组)与不等式(组)部分:分为一元一次方程,二元一次方程组,不等式与不等式组,一元二次方程,分式方程这五个主要分支,每个主要分支再细分为概念、解法、应用等。学生理清了知识框架,复习也就起到了事半功倍的效果。
“双结构”模式教学要求教师对“教材知识”和“方法程序”的概括化、结构化。在教学中,教师吃深、吃透,学生悟深、悟透。借助于思维导图的神助攻,形成知识体系,提高逻辑思维能力。让我们学生的学习化被动为主动,积极思考、参与,让我们的课堂真正成为生本的课堂、灵动的课堂!

