一种预测特高含水期开发指标的联解法
张继成,范佳乐,匡 力,张 军,吕冰玉
东北石油大学石油工程学院,黑龙江大庆 163318
水驱或边水驱油田进入特高含水期后,用于预测开发指标的水驱特征曲线会发生向上偏折,从而导致预测的含水率等开发指标低于实际值,不利于油田后期的生产指导及开发调整[1-2].于波等[3-5]研究发现, ln(Kro/Krw)-Sw曲线(Kro为油相相对渗透率;Krw为水相相对渗透率;Sw为含水饱和度)在特高含水期在半对数坐标上偏离原来的直线关系,转而向下弯折,是导致水驱特征曲线在特高含水期发生上翘的根本原因.
为正确地预测特高含水期的开发指标,需要重新对渗流特征方程进行拟合,刘世华等[6-7]从油水相对渗透率比曲线特征出发来改进现有的渗流特征方程,使曲线出现了下弯,并根据新的渗流特征方程推导出了一种新型的水驱特征曲线.朱圣举等[8-10]对基于Arps提出的指数递减、双曲递减和调和递减3种经典类型进行深入研究,并应用于实际的油田开发中.陈元千等[11-12]将Arps中的t改为t-t0后得到了适用于无峰、单峰、双峰和均峰等不同开发模式广义的指数递减、双曲递减和调和递减型.姚建等[13-14]对Arps递减规律和甲型水驱曲线的相关性进行了研究.王俊魁等[15-16]将广义翁氏模型、Hubbert模型与水驱曲线分别进行了联立求解,建立了含水率与时间的关系.崔传智等[17-19]将水驱特征曲线与Arps递减规律巧妙地结合,得到了产量递减以后的开发指标预测模型,该模型能够预测产量递减后不同开发时间对应的含水率、产油量和采出程度等指标,为油田开发的决策提供了极大的便利.
本研究基于高丽等[20-22]提出的二段直线法,将其与Arps递减规律相结合,得到第2段水驱特征曲线对应的含水率模型及采出程度模型,该模型能够预测不同开发时间对应的含水率及采出程度指标,并且模型的参数容易被求解,得到的模型能够直线外推,实用性较强.
1 甲型水驱特征曲线第2直线段方程
根据实际的相渗曲线,计算不同含水饱和度对应的相对渗透率比值,将其绘制在半对数坐标上,首先拟合出曲线上第1直线段的方程,得到其斜率b1和截距a1; 然后标定第1直线段发生偏折的点M的坐标,即第2直线段的起点;对高含水期的弯曲段数据进行线性拟合,得到第2段直线的方程,从而得到该直线的斜率b2与截距a2. 具体过程见图1.其中,Kro为油相相对渗透率;Krw为水相相对渗透率;Sw为含水饱和度;Swe为出口端含水饱和度;a1为第1直线段延长线在纵轴上的截距;b1为第1直线段的斜率;a2为第2直线段延长线在纵轴上的截距;b2为第1直线段的斜率.
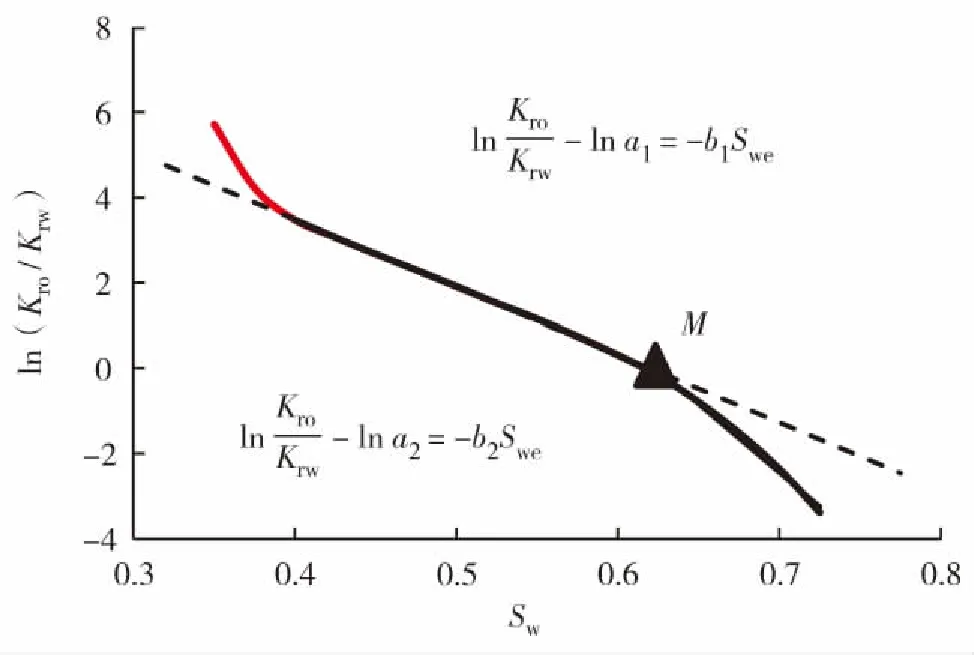
图1 ln(Kro/Krw)-Sw曲线Fig.1 (Color online) The relationship curve of ln(Kro/Krw)-Sw
将M点的坐标(Swe,Kro/Krw)代入分流量方程中,可以求得转折点对应的含水率fw.
将油井的累积产油量与累积产水量的对数绘制在坐标上,拟合出甲型水驱特征曲线的第1直线段的方程为
lgWp=A1+B1Np
(1)
其中,Wp为累积产水量;Np为累积产油量;A1为甲型水驱特征曲线第1直线段截距;B1为甲型水驱特征曲线第1直线段斜率.
将式(1)适当变形并两边同时对Np求导,得
(2)
其中,Rwo为水油体积比;fw为含水率(体积分数).
根据水油比的定义,将式(2)进一步变形,得
(3)
将式(3)的变量和自变量互换,可得

(4)
根据二段直线法的理论基础,油水相渗比值的对数与含水饱和度的关系式的转折点M, 对应图2所示的水驱特征曲线的转折点M′.
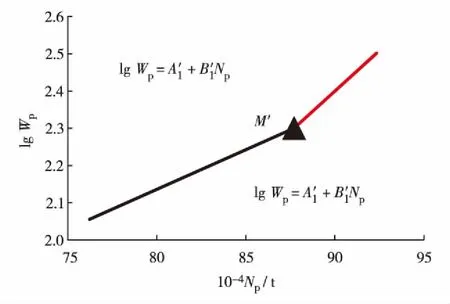
图2 甲型水驱规律曲线Fig.2 (Color online) Water flooding characteristic curve of A-type
将油水相渗比值的对数与含水饱和度的关系式的转折点M的含水率代入式(4),可以求得水驱特征曲线转折点M′点的横坐标Np, 再将该Np的值代入水驱特征曲线的第1直线段,可计算出水驱特征曲线的转折点的纵坐标Wp.
由甲型水驱特征曲线的推导过程可知,第1与第2直线段斜率的计算表达式中含有相同的因子,故将两者相比,约去公因子,根据已得到的第1直线段的斜率,求得第2直线段斜率为
(5)
其中,B2为甲型水驱特征曲线第2直线段斜率.
转折点M′既是第1直线段的终点,又是第2直线段的起点,因此其坐标同时满足两直线段,将转折点M′的坐标以及甲型水驱特征曲线第2直线段的斜率代入第2段直线方程中,即可求得第2直线段的截距A2为
A2=lgWp-B2Np
(6)
其中,A2为甲型水驱特征曲线第2直线段截距.
从而得水驱特征曲线第2直线段的方程为
lgWp=A2+B2Np
(7)
2 折线法检验
本研究预测水驱特征曲线第2直线段时,用到了折线法.该方法成立的基础是油水相渗比值的对数与含水饱和度的曲线转折点与水驱特征曲线的转折点存在对应关系.
折线法首先利用油水相渗比值的对数与含水饱和度的关系式的转折点对应的含水率,结合水驱特征曲线第1直线段的方程,预测水驱特征曲线发生转折的坐标,然后根据油水相渗比值的对数与含水饱和度关系式两段直线的斜率,以及水驱曲线第1直线段的斜率,得到水驱曲线第2直线段的斜率,从而结合转折点的坐标,得到水驱特征曲线第2直线段的方程.
为验证折线法的正确性,首先利用大庆油田10口油井的累积产油量与累积产水量对数的关系曲线,做出各自相应的水驱特征曲线,然后找出其上翘点对应的含水率,结果如表1.

表1 水驱特征曲线的上翘点对应含水率Table 1 The upward point of water drive characteristic corresponding water content %
由表1可见,这10口井的水驱特征曲线上翘点对应的含水率分布在90.58%~96.49%,平均值为93.49%.然后根据这10口井的相对渗透率数据,绘制油水相渗比值的对数与含水饱和度的关系曲线,再由该曲线找到转折点对应的含水率为93.37%.可以看出,油水相渗比值的对数与含水饱和度的关系曲线转折点对应的含水率与水驱特征曲线对应的含水率相差无几,从而验证了折线法的正确性.
3 Arps产量递减规律
油田开发过程中,随着地下能量的变化和可采储量的减小,产油量总是要下降的,通常用递减率表示产量的递减速度,产量递减率D为
(8)
其中,q为产量;t为递减时间;n为递减指数, 0≤n≤1;k为比例常数.
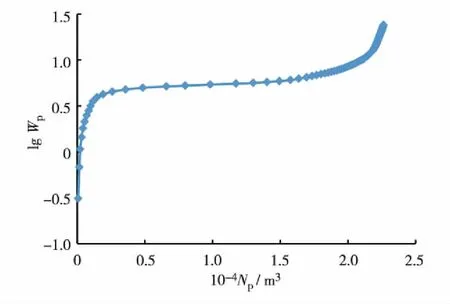
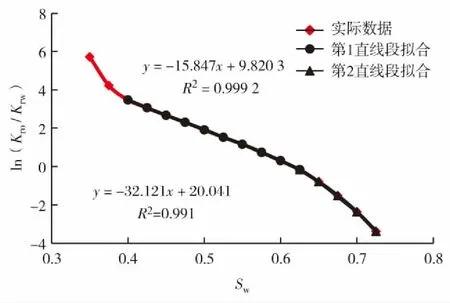
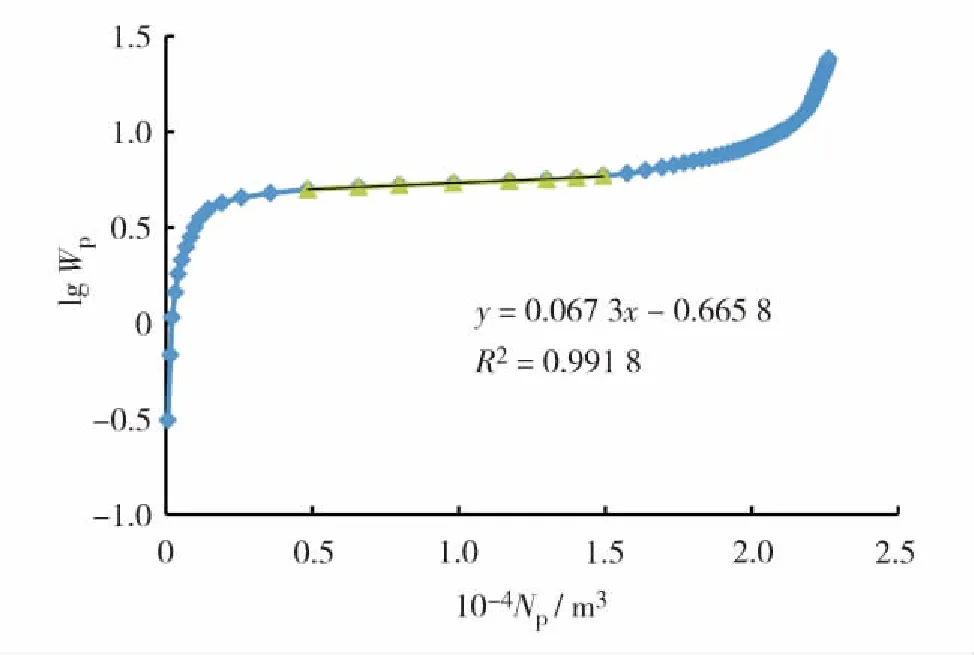
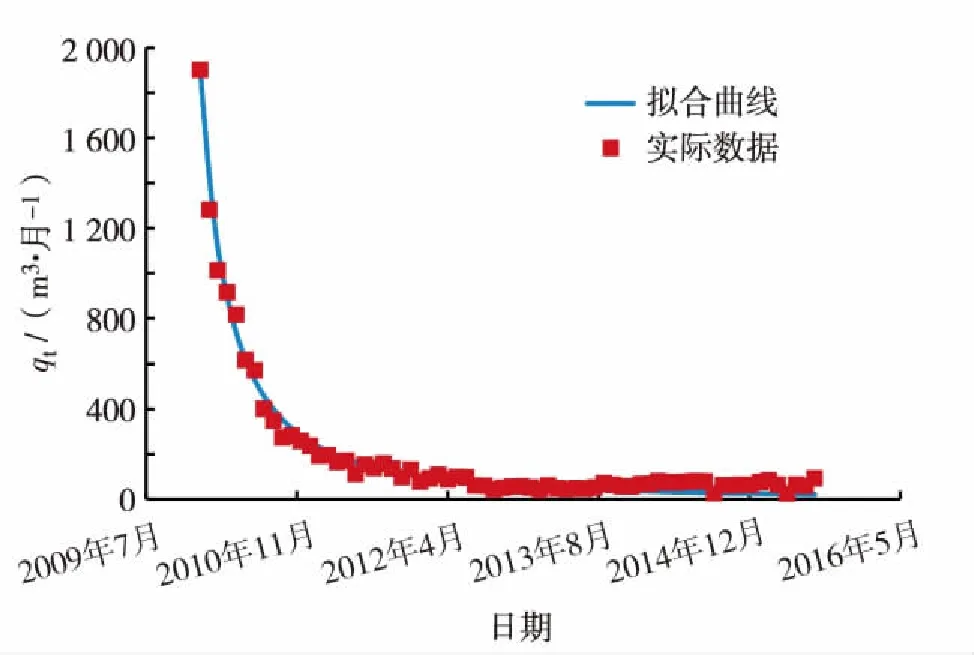
当0 (9) 其中,qi为递减初始产量;qt为递减后t时刻产量. 由式(8)可知 (10) 其中,Di为初始递减率. 将式(10)代入式(9),变形后可得如式(11)所示的双曲线型递减曲线的产量随时间变化关系. (11) 对式(11)两端进行t积分,得递减期间累积产油量为 (12) 通常情况下,水驱特征曲线发生向上偏折对应的含水率均在95%以上,而产量递减时的含水率达不到如此高的数值,且后期含水率的上升速度逐渐变慢,故可以认为产量递减的发生时间早于水驱特征曲线发生向上偏折的时间,因此,水驱特征曲线的第2直线段完全处于产量递减期. 基于上述推论,可得到不同开发时间对应的累积产量为 (13) 其中,Np0为递减初始累积产量;t0为递减初始时间. 以上是Arps递减规律的双曲线递减曲线对应的产量及累积产量公式的推导过程.实际运用时,可根据产油量曲线,找出产量递减的起始时间,然后结合线性试差法,对递减期间的产量公式进行拟合,得到产量和累积产量中的参数:递减指数n, 初始递减率Di的值,再代入式(13)中,得到累积产量公式. 含水率可根据分流方程求得,分流量方程为 (14) 其中,μw为水相黏度;μo为油相黏度. 第1段直线方程代入式(14),可得 (15) 将式(15)变形可得 (16) 对式(14)两端出口端含水饱和度求导,可得 (17) Welge方程[23]如下 (18) (19) 根据采出程度的定义,有 (20) 其中,R为采出程度;Swi为原始含水饱和度. 将式(19)代入式(20),可得水驱特征曲线第1直线段对应的采出程度与含水率之间的函数关系为 R= (21) 首先,给出一个比水驱特征曲线转折点M′对应的累积产量小的累积产量值,代入式(3)求得对应的含水率.然后,将该含水率fw代入式(21)中,求得对应的采出程度.此时,同一个点对应的采出程度和累积产量均已求出,根据式(22),能够校准地质储量N. (22) 根据式(1)至式(3)方法,得到水驱特征曲线第2直线段对应的含水率与累积产量的表达式为 (23) 将式(13)代入式(23),得到含水率与开发时间的关系为 fw=1- (24) 将式(22)代入式(13),得到采出程度与开发时间的关系为 (25) 以大庆油田某油井为例,为判断该油井是否需要用折线法推导其水驱特征曲线第2直线段,根据大庆油田某油井的累积产油量与累积产水量的对数对应关系,得到如图3所示的甲型水驱特征曲线.由图3可知,该油井对应的水驱特征曲线已经出现了第2直线段,因此不需要用折线法对第2直线段进行预测,直接拟合即可. 图3 大庆油田某口油井的甲型水驱特征曲线Fig.3 (Color online) A-type water flooding characteristic curve of a well in Daqing Oilfield 图4 水驱特征曲线第2直线段拟合Fig.4 (Color online) Fitting of the second straight line of the water flooding characteristic curve 图5 油水相渗比值的对数与含水饱和度关系曲线拟合Fig.5 (Color online) The fitting of the curve between the logarithm of oil water relative permeability ratio and water saturation 为校准地质储量,首先需要得到油水相渗比值的对数与含水饱和度的关系式的第1直线段斜率和截距,拟合的油水相渗比值的对数与含水饱和度的关系曲线如图5.根据拟合结果,得到油水相渗比值的对数与含水饱和度的曲线第1直线段和第2直线段相关参数,其中,第2直线段的相关系数为0.991,符合拟合精度要求,第1段直线的相关参数a1=18 403.57;b1=15.847;Swi=0.318 8;μw/μo=0.083. 为求得水驱特征曲线第1直线段上不同的点对应的含水率,需要拟合出第1直线段的方程,拟合曲线如图6. 图6 水驱特征曲线第1直线段拟合Fig.6 (Color online) Fitting of the first straight line of the water-flooding curve 选取井史数据中累积产油量为0.982 6×104m3的数据点,根据式(3)求得该点对应的含水率为45.50%,将该含水率代入式(21)中可得采出程度为19.44%,根据累产油量和采出程度的计算结果,可得到校准的地质储量为5.053 6×104m3. 为了得到该井的产量递减规律,首先利用线性试差法与最小二乘法,对该井的产量递减期间的产油量曲线进行拟合,得到的拟合曲线如图7. 图7 产量递减期间产量拟合Fig.7 (Color online) Production fitting during declining production 根据拟合结果,得到产量递减拟合曲线相关参数n=0.57;Di=0.314 4;qi=0.190 2;Np 0=0.982 6. 将上述计算结果代入式(24)和式(25),得预测含水率与采出程度的模型为 (26) R=0.194 443 196-0.278 423 157×[(1+0.179 2×(t-t0))-0.754 385 965-1] (27) 由于甲型水驱特征曲线第2直线段拟合的最后数据点为2013年3月,因此,从2013年4月开始,用式(26)和式(27)所示的含水率与采出程度计算模型,计算不同开发时间对应的开发指标,得到的结果为该模型的预测值.通过将含水率预测值与实际值进行对比计算后,得到其含水率的平均误差值为1.306%,由此可见,其含水率的预测精度很高,预测值和实际值的差值较小.通过将采出程度预测值与实际值进行对比并计算后,采出程度的平均误差值为4.950%,采出程度的预测精度较高,预测值和实际值的差值较小. 综上研究可知: 1)本研究首先利用折线法推导出了甲型水驱第2直线段的方程,并通过实际数据验证了折线法的正确性,之后结合Arps递减规律得到了特高含水期开发指标的计算模型,并且用该模型对开发指标进行预测,含水率月平均误差为1.306%,采出程度月平均误差为4.950%,总体精度较高. 2)水驱特征曲线发生向上偏折对应的含水率均在95%以上,而产量递减时的含水率达不到如此高的数值,且后期含水率的上升速度逐渐变慢,可以认为,产量递减的发生时间早于水驱特征曲线发生向上偏折的时间,可见水驱特征曲线的第2直线段完全处于产量递减期,本研究通过利用线性试差法与最小二乘法拟合得到了递减阶段的拟合曲线. 3)通过水驱特征曲线得到上翘点对应的含水率为90.58%~96.49%,平均值为93.49%,折线法得到的转折点的含水率为93.37%,这与水驱特征曲线法得到转折点的含水率相差无几,从而验证了折线法的正确性.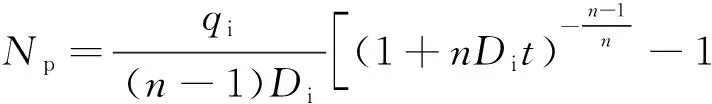
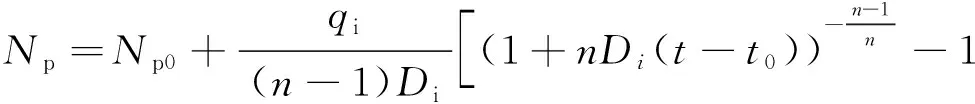
4 特高含水期指标预测模型
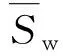
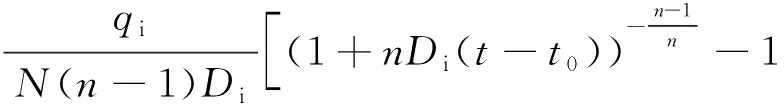
5 特高含水期开发指标计算算例



6 结 论

