预测水平井携液临界气流速的新模型
刘永辉,艾先婷,罗程程,刘丰伟,吴朋勃
1)西南石油大学石油与天然气工程学院,四川成都 610500;2)中石油玉门油田勘探开发研究院,甘肃玉门 735200
积液是气井生产中后期普遍遇到的问题.在气藏开发过程中,地层压力不断下降,气井产量逐渐降低.当气井产量降低到某一值时,气体不能将液体从井筒中带出导致液体在井筒中累积,造成积液,影响生产[1-4].因此,准确预测气井积液对于保证气井正常生产具有重要意义.
目前,中国各大气田中应用最广泛的携液临界气流速预测模型是TURNER等[5]基于圆球形液滴提出的液滴反转模型,出于安全考虑,其安全系数取1.2.COLEMAN等[6]对现场积液气井研究后发现,对于油压低于3.5 MPa的气井,不加安全系数,模型精度更高.李闽等[7]认为液滴受力后会变形,从而基于椭球体液滴建立了新的携液临界气流速模型,其计算值仅为TURNER模型的1/3.此外,许多学者也基于液滴受力分析开展了广泛的研究[8-14].尽管液滴模型应用广泛,其携液机理却缺乏验证.WESTENDE等[15]的实验证明液滴尺寸远小于模型假设值;ALAMU[16]研究表明,环状流/搅动流转变时,液滴夹带率小于5%,液体大部分以液膜形式向上携带.此外,液滴在倾斜段中难以长时间运移.因此液膜反转模型能够更加准确解释气井积液[17-18].然而,目前基于液膜反转的携液气流速模型较少.BELFROID等[19]对液膜反转时气井积液机理进行研究,提出了倾斜角修正公式,但其模型仍采用TURNER模型的形式;LUO等[20]基于BARNEA[21]所提出的液膜模型建立了水平井携液临界气流速模型,但模型复杂,现场难以运用.为此,本研究开展了基于液膜反转的携液临界气流速测试实验,分别研究了油管与水平夹角(θ,以下简称角度)、 油管内径(D)和液体表观流速对携液临界气流速的影响规律,并提出了基于液膜反转的携液临界气流速经验公式.
1 实验装置及方法
1.1 实验装置
为深入研究水平井临界携液规律,本研究研制了一套可视化的气水两相流动模拟实验装置,用以开展不同角度下气液流动实验.实验系统由进气系统、进水系统、管路系统和测控系统4部分组成,流程如图1.实验管段主体长5 m,采用透明有机玻璃管组成,管段主体可拆卸组装不同管径玻璃管;且可通过改变支架的倾角来改变倾斜管的角度,从而模拟水平井中不同的角度下气液流动情况.实验介质为空气和水,测量不同倾角下气井的携液临界气流速.
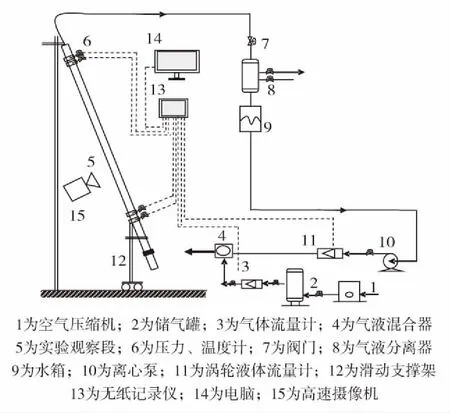
图1 实验流程图Fig.1 Schematic of the experimental flow loop
1.2 液膜反转确定
本研究以液膜反转作为积液起始点.实验时,液膜反转采用高速摄像仪追踪液膜中紧贴管壁所夹带的气泡运动轨迹进行判断.在D=30 mm的油管中,液体表观流速vsl=0.03 m/s,当气体表观流速vsg=14.50 m/s时,液膜中夹带的气泡流动方向发生改变,出现回流现象(图2),即可认定液膜发生反转,与之对应的气流速可认为携液临界气流速.

图2 液膜反转图(vsl=0.03 m/s, vsg=14.50 m/s)Fig.2 (Color online) Liquid film reversal(vsl=0.03 m/s, vsg=14.50 m/s)
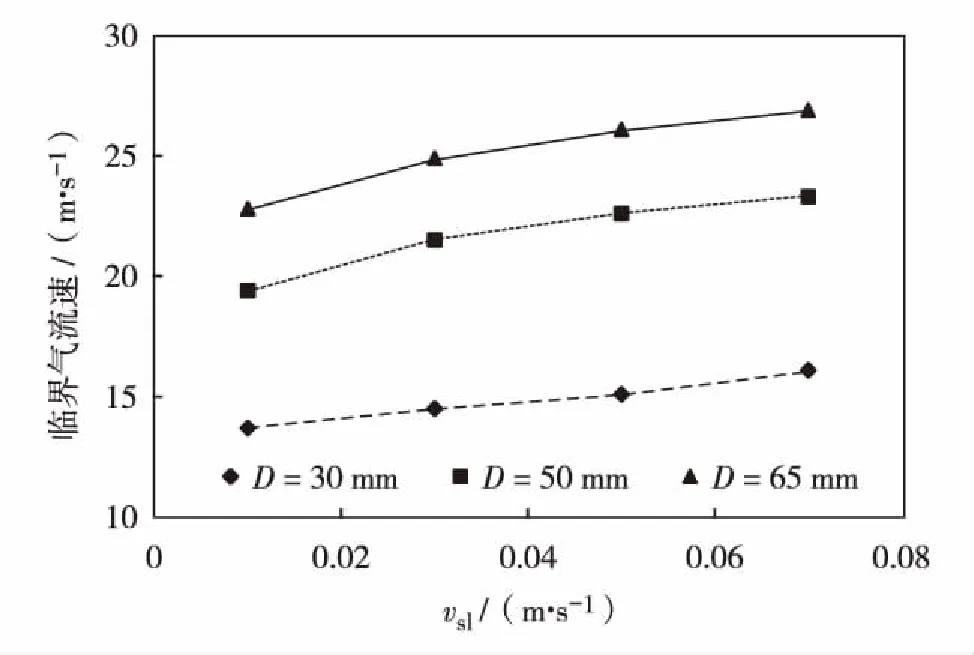
图3 不同管径下携液临界气流速随液体表观流速变化曲线(θ=90°)Fig.3 The curve of critical gas velocity with apparent liquid velocity under different pipe diameters (θ=90°)
2 实验结果与分析
图3为垂直管(θ=90°)中,不同管径(D)下携液临界气流速随液体表观速度的变化关系.随着液体表观速度的增加,井筒液膜厚度增大,导致维持液膜向上而不反转的气量增加,即携液临界气流速增大.不同管径下,携液临界气流速与液体表观流速近似呈线性关系.而从携液临界气流速随油管内径的变化关系(图4)来看,油管内径越大,携液临界气流速越大.由WALLIS[23]提出的气-液内剪切力公式可知,管径与内摩擦力成反比,管径越大则内摩擦力越小,气体对液膜的曳力越小;相同液膜厚度下,管径越大所需携液临界气流速则更大.

图4 不同液流速下携液临界气流速随油管尺寸变化曲线(θ=90°)Fig.4 The curve of critical gas velocity with tubing size under different liquid velocities(θ=90°)
图5为液体表现流速vsl=0.01 m/s时,不同管径下临界气流速随角度变化曲线.由图5可知,随着角度增加,临界气流速先增后减,在θ≈55°时携液临界气流速最大,这与BELFROID所提出的角度修正项变化趋势一致.随后,基于垂直段所得到携液临界气流速,采用BELFROID角度修正项对D=30 mm的油管在不同角度时的携液临界流速进行计算,并与实验值对比,结果如图6.实验值与BELFROID角度修正项计算值吻合度非常高,误差仅为2.09%.因此,在已知垂直段携液临界气流速时,可通过BELFROID角度修正项对不同角度携液临界气流速进行计算.
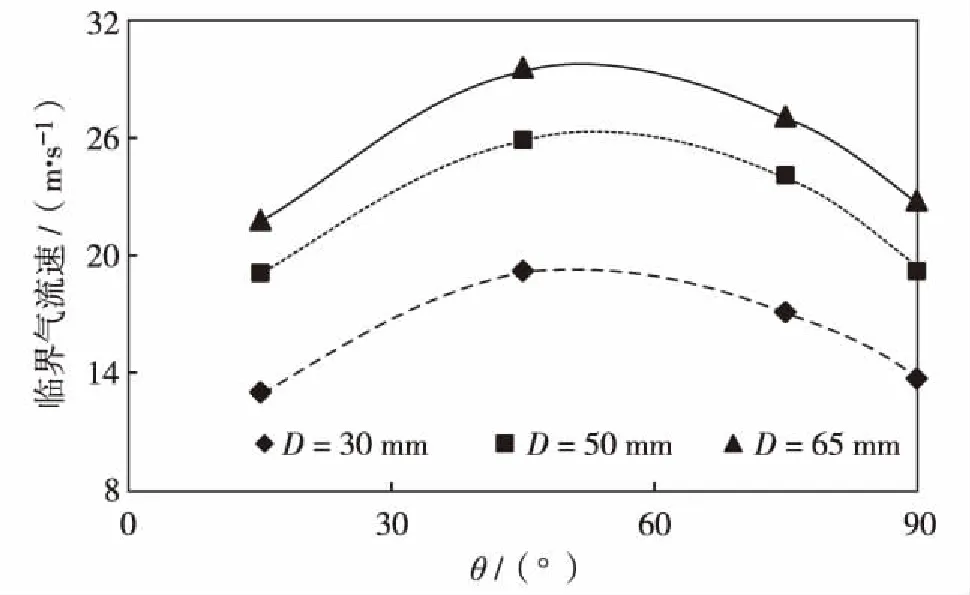
图5 不同管径下携液临界气流速随角度变化曲线(vsl=0.01 m/s)Fig.5 The curve of critical gas velocity with angle under different pipe diameters (vsl=0.01 m/s)
携液临界气流速随角度的增加而先增后减,这主要是由于当液膜开始反转时,管壁对液膜的摩擦力为0,液膜重力轴向分量完全由气芯所提供曳力支撑.气体对液膜的曳力如式(1)所示.在实验过程中,可观察到随着角度增加,液膜沿着管道内壁周向分布更加均匀,管道内壁周向底部液膜则更薄(图7).其中,τw为气液界面剪切力;G为管壁底部液膜重力.这与GERACIA等[22]的实验结果一致(表1).
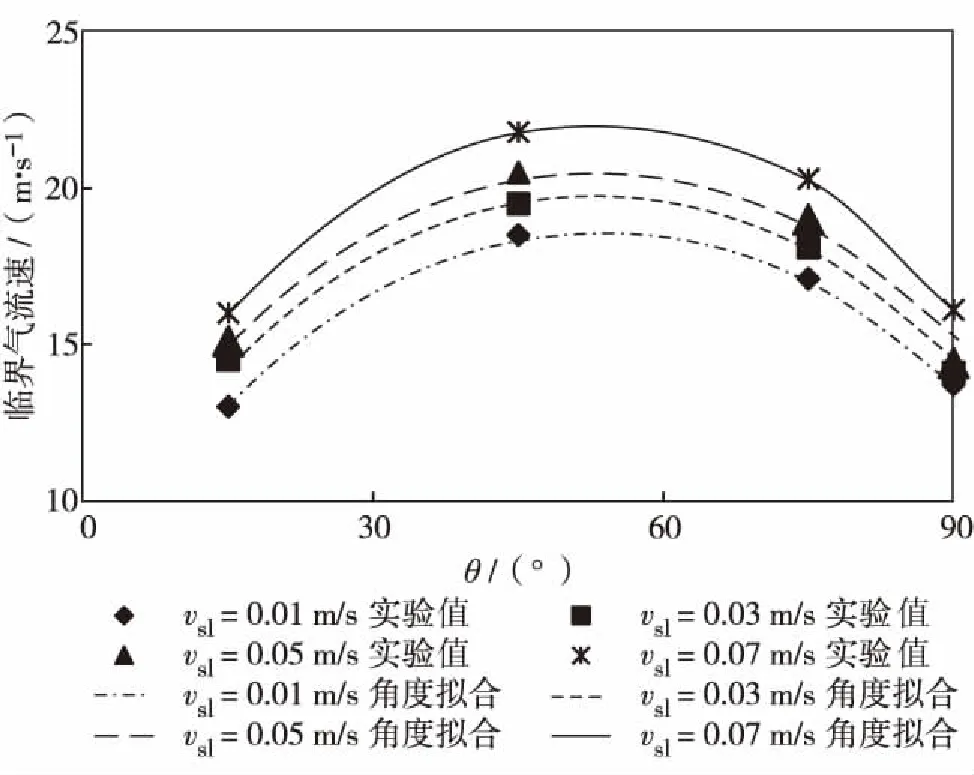
图6 实验值与BELFROID角度修正项计算值对比(D=30 mm)Fig.6 Comparison between the measured and the predicted critical gas velocities(D=30 mm)
Fg=Gsinθ
(1)
其中,Fg为气体对液膜的曳力;G为液膜重力.
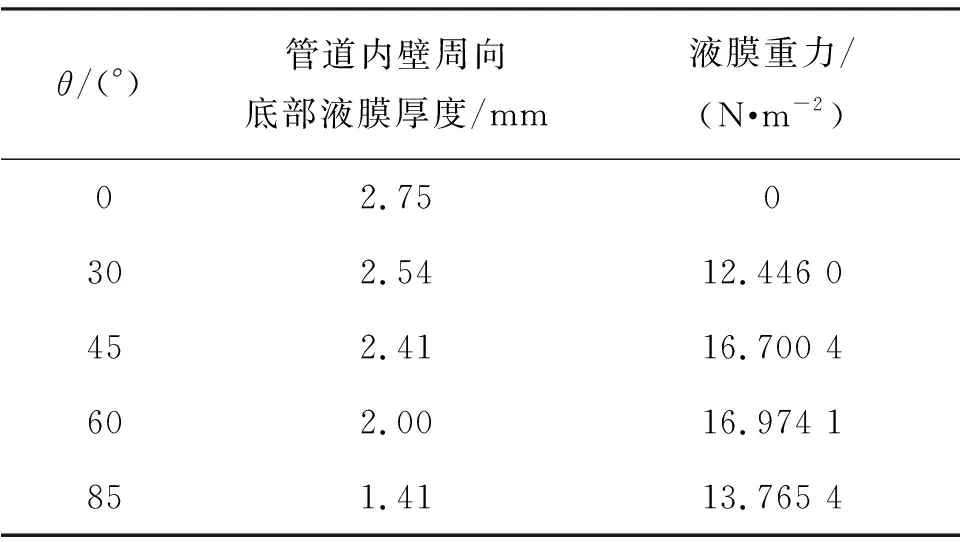
表1 不同角度下的液膜厚度与单位面积管道内壁周向液膜重力1)Table 1 Liquid film thickness and gravity at different angles
1)D=38.1 mm,vsl=0.011 m/s,vsg=21.500 m/s
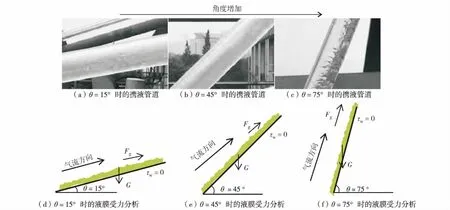
图7 不同角度下液膜受力分析Fig.7 (Color online) Schematic of the force balance on the liquid film at the bottom of an inclined pipe
图8展现了液膜受力与角度关系.其中,正弦值为式(1)中的sinθ,表示液膜重力沿管道轴向的分量.由图8可知, 随着角度的增加, 液膜重力的轴向分量先增大后减小.因此,当θ≈55°时气体所需曳力最大.
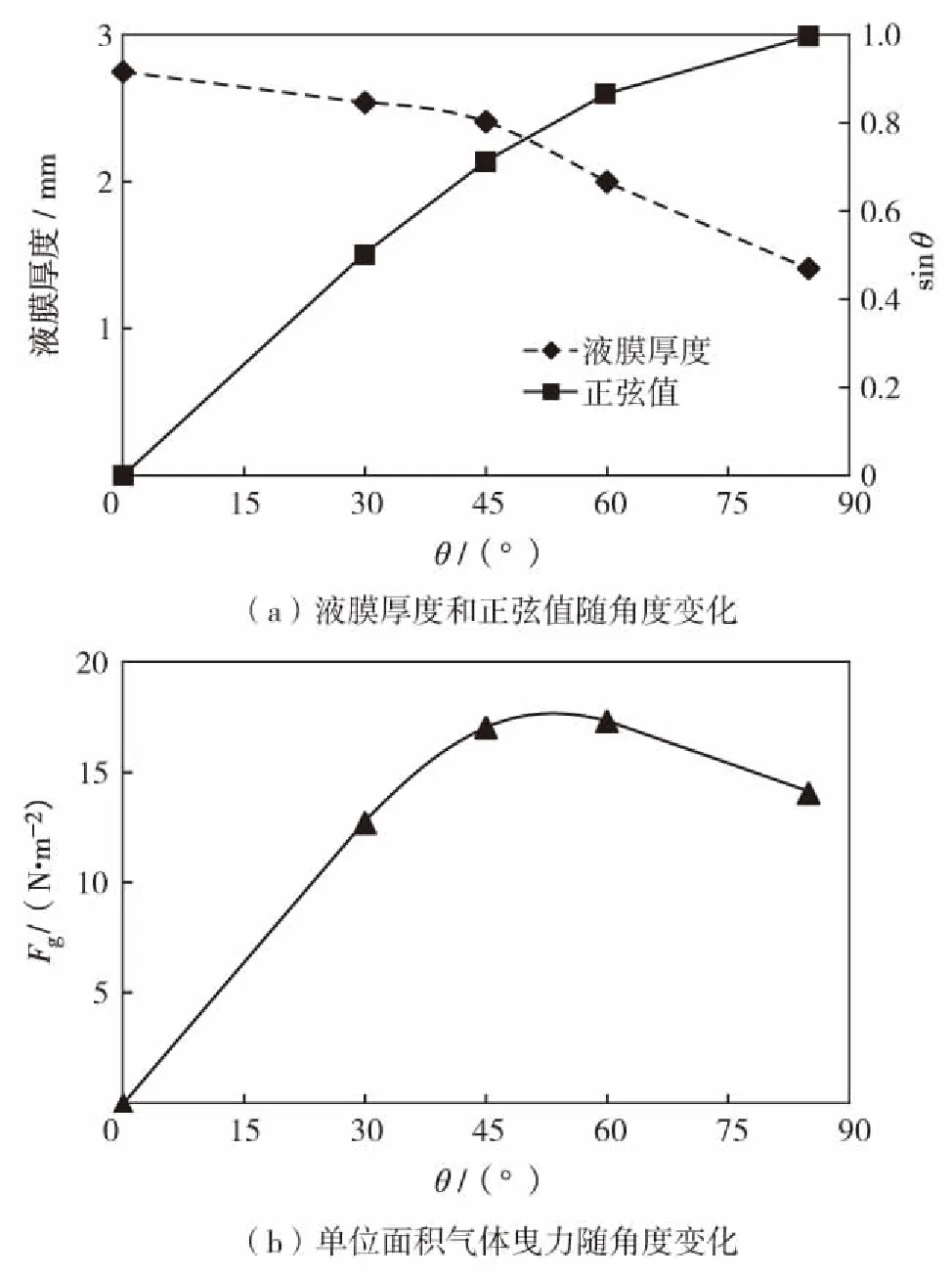
图8 不同角度下液膜受力变化情况Fig.8 The curve of liquid film at different angles
3 新模型的建立及验证
本研究基于实验实测数据,考虑了油管内径和液量的影响,结合角度修正关系拟合了新的携液临界计气流速计算公式,并利用文献数据对新模型进行了验证.
3.1 模型建立
1969年,WALLIS等[23]提出如式(2)的液泛经验公式,可用作液膜反转界限判定.
(2)
其中,vsg为气体表观流速;ρL为液体密度;ρg为气体密度;m为变量参数;vsl为液体表观流速;g为重力加速度,本研究设g=9.81 m/s2;C为常数.
由于气井日产液量较小,液体表观流速极小,通常可忽略液体流速对液膜反转的影响,因此式(2)可简化为
(3)
图3结果表明,θ=90°时,携液临界气流速与液体表观流速近似呈线性关系.为此,增加液体表观流速的影响,在式(3)中添加液相影响项可得
(4)
其中,a为变量参数.
倾斜管不同角度下的临界携液气流速可根据相同管径和液体表观流速下垂直段所对应携液临界气流速进行BELFROID角度修正项获得,即水平井携液临界气流速计算模型

[sin(1.7θ)]0.38/0.74
(5)
结合实验数据,使用1stOpt软件对式(5)中的参数进行迭代拟合,得到水平井携液临界气流速计算公式为
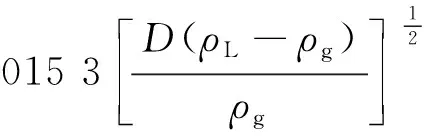
(1+3.103 8vsl)[sin(1.7θ)]0.38
(6)
利用新模型对实验数据进行评价,结果如图9.由图9可知,模型计算值与实验值吻合度高达94.96%.
3.2 模型验证
基于文献[24]公布的44口垂直井数据(请扫描论文末页右下角二维码查看表1),分别采用本研究建立的新模型和TURNER模型预测积液情况,得到如图10的对比结果.该44口井均为积液井,因此计算结果应全部落在积液区域.由图10可知,TURNER模型预测准确率为52.27%,有21口井落在未积液区域,而新模型计算准确度为95.45%,只有2口井落在未积液区域.

图10 COLEMAN数据下不同模型计算结果对比图Fig.10 (Color online) Comparison of calculated gas velocity by different models with field data of COLEMAN
基于文献[25]公布的67口积液水平井基础数据(请扫描论文末页右下角二维码查看表2),分别采用本研究建立的新模型和BELFROID模型预测积液情况,得到如图11的对比结果.由图11可知,BELFROID模型预测准确率仅为17.91%,而新模型的预测准确率达80.59%,仅13口井落在未积液区域,预测准确率较BELFROID模提高了62.68%
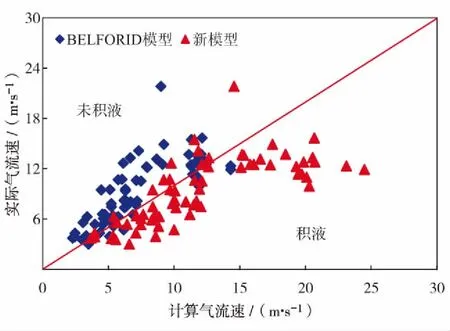
图11 VEEKEN数据下不同模型计算结果对比图Fig.11 (Color online) Comparison of calculated gas velocity by different models with field data of VEEKEN
表4为垂直井与水平井预测结果比较.统计结果表明,新模型对垂直井和水平井的临界携液气流速预测准确率均高于工程常用模型.
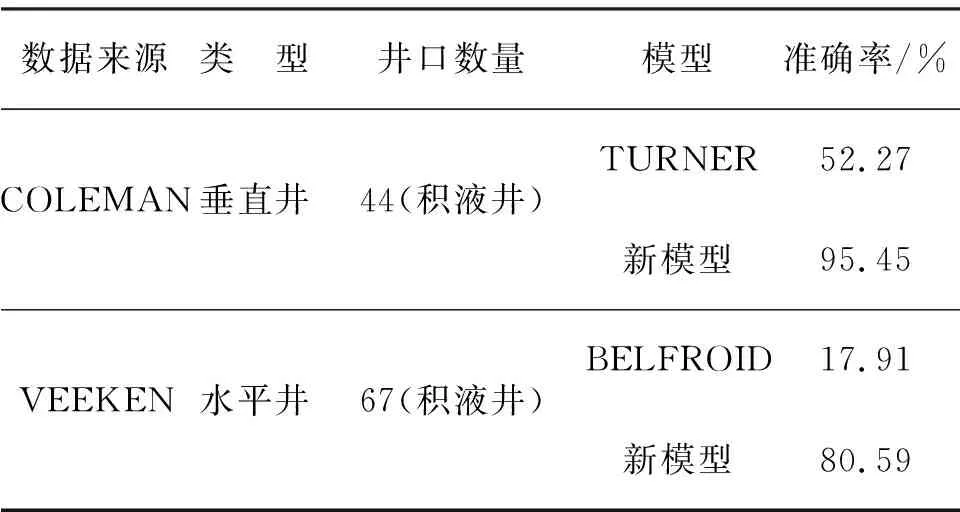
表4 模型预测结果比较Table 4 Comparison of model prediction results
4 结 论
1)携液临界气流速随着液体表观流速增加而增大,其变化趋势近似呈线性关系;携液临界气流速随着油管内径增加而增大;
2)基于垂直管携液临界气流速测试数据,BELFROID角度修正关系可用于计算不同倾角下的临界携液值,与实验误差仅为2.09%;
3)建立了一种计算水平井携液临界气流新模型,模型验证结果表明,新模型预测COLEMAN发表的44口积液直井准确率为95.45%,VEEKEN发表的67口积液水平井准确率为80.59%.

