基于波前编码技术的眼底成像系统

金易弢, 张 薇

(上海理工大学 光电信息与计算机工程学院, 上海 200093)

引 言

视网膜作为一层结构非常复杂的薄膜,是人眼结构中十分重要的组成成分,在眼球中起到的作用相当于光学系统中的图像接收面。在医学上,对眼底的血管网络进行观测,可以用于诊断出相关眼部疾病,另外,还可以作为全身疾病的早期诊断依据,如冠心病、糖尿病、高血压等。

在眼底成像系统的设计中,需要考虑人眼的光学结构对成像质量的影响,因此需要通过校正人眼像差获得高分辨率的眼底图像。为了解决人眼像差对眼底成像的影响,文献[1]引入自适应光学系统,在该系统中使用波前检测器来检测眼睛的像差,然后用一个与眼睛像差相反的相位板来补偿像差。然而自适应光学系统需要对不同的人眼系统进行不同的波前像差检测和校正,系统复杂而且昂贵,从而限制了该系统的可用性。

1995年,Dowski等在解决红外成像系统随温度变化产生的图像离焦问题时,采用模糊函数和静态稳像法,并基于傅里叶光学理论提出了波前编码[2],该技术通过改造成像系统的光瞳,在不降低系统截止频率的同时,使得系统的光学传递函数(OTF)/点扩散函数(PSF)在一定的离焦范围内保持非常高的一致。和传统的光学系统对比,该成像系统的不同频率的信息分量的对比度会由于在光瞳位置添加的相位掩膜板而降低[3-4],所以波前编码系统会得到模糊的中间像,通过数字解码复原,将该模糊图像解码恢复为清晰图像。Arines等把波前编码技术引入到眼底成像系统中[5],他们通过在光学系统的出瞳位置添加一块面型为Ar3cos(3θ)的相位板对眼底图像进行编码,然后用维纳滤波解码算法复原得到清晰的眼底图像,该成果表明了波前编码技术可以补偿人眼的离焦像差,但是该面型的相位板对像散、彗差等其他人眼像差的作用有限,得到的眼底图像仍然有形变。

本文提出并设计了一款采用波前编码技术补偿人眼像差的便携式眼底成像系统。在该系统中成像光路和照明光路共享一块物镜,并在成像系统的出瞳位置放置一块三次型Z=α·(x3+y3)相位掩膜板[6],这种结构可以减少传统眼底相机中为补偿眼底像差而设计的光学元件,从而提高眼底相机的可便携性。通过理论分析和实验仿真,证明了该相位板能使眼底成像对人眼的离焦和其他高阶像差不敏感,并通过维纳滤波复原得到高分辨率的眼底图像。

1 基于三次相位板的波前编码成像系统

波前编码技术使用特定的光学元件或者光学系统作为编码元件,该元件可以使系统的光学传递函数不受与离焦相关的像差影响[8-9]。 波前编码系统包括一个记录编码图像的过程和一个图像解码的后处理步骤,图1为波前编码技术的处理过程。

图1 波前编码技术的处理过程Fig.1 Wave-front coding processing

当成像物体偏离对准平面,或者成像传感器偏离景象平面,都会产生离焦现象。系统中产生严重的离焦时,成像图像会产生严重的退化和模糊,其中系统离焦的程度可以用离焦量来定量表示[10],即

(1)

式中:ψ为离焦量,以弧度π为单位;f为成像系统的焦距;d0和d1分别为物距和像距;D为透镜孔径直径;λ为光波长;W20为离焦产生的最大波像差。

广义光瞳函数可以表示系统所具有的像差,此处离焦像差为

(2)

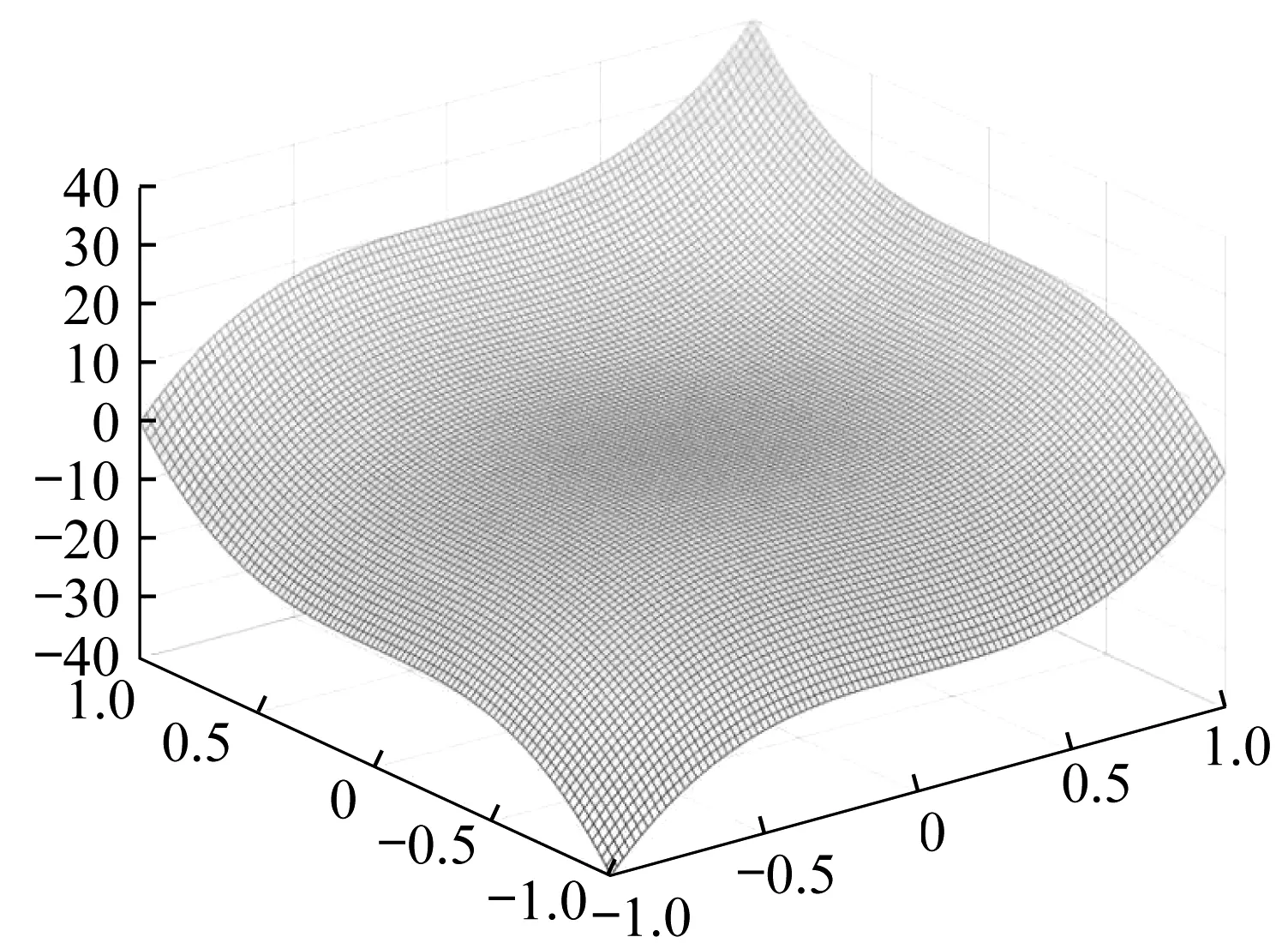
图2 三次相位板结构图Fig.2 Cubic phase plate structure

对于三次相位板系统(如图2),其孔径函数可以表示为

(3)

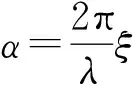
当系统孔径平面中引入式(3)表示的三次相位掩膜板后,此时的广义光瞳函数可以表示为

(4)

光学传递函数(OTF)可以表示成像质量的好坏,其表达式为

(5)

式中:u是归一化的空间频率;x是孔径平面水平方向归一化坐标;*表示复共轭。将式(4)代入式(5),并进行化简可以得到引入三次相位板后系统的离焦OTF为

(6)

利用稳相法对式(6)进行近似求解,得到

(7)

由式(7)可以得到引入三次相位板系统的离焦调制传递函数(MTF)为

(8)

由式(8)可知,引入三次相位掩膜板的波前编码系统的离焦MTF与离焦波像差W20无关,这说明通过引入三次相位板可以有效改变光学系统的OTF使得其对离焦量不敏感。

2 图像反卷积及维纳滤波算法

设计了一个具有波前编码功能的光学成像系统后,物体通过该编码系统在图像探测器上会得到一张模糊的图像。为了获得大景深的清晰图像,还需要对模糊图像进行解码操作,即图像的反卷积复原。

从傅里叶变换域的角度分析,系统对物平面的退化过程实质上是一个低通滤波的操作,反卷积操作的目的就是通过研究点扩散函数(PSF)的规律以及观测图像,找到成像过程中丢失的高频部分从而提高图像的清晰度,但由于成像过程中存在噪声的影响,所以图像复原问题也就是在反卷积和噪声放大之间寻求最优解的问题。在解决反卷积图像复原问题中,维纳滤波是一个最经典的处理办法[11],其基本的思想如图3所示。

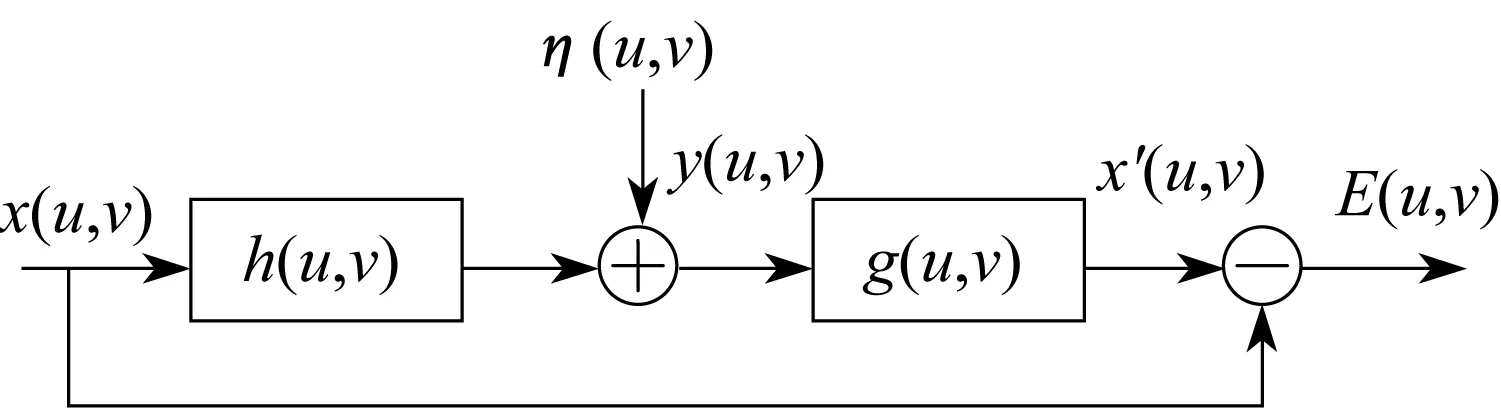
图3 维纳滤波器原理图Fig.3 Wiener filter schematic

对于一个离散化的二维卷积过程,可以表示为

y(u,v)=x(u,v)*h(u,v)+η(u,v)

(9)

式中:*表示二维卷积操作;x(u,v)表示输入图像;h(u,v)表示卷积核;η(u,v)表示噪声;y(u,v)表示输出图像。

维纳滤波算法试图找到一个滤波器g(u,v),当由式(9)得到的卷积输出图像y(u,v)输入该滤波器后,系统的输出为

(10)

滤波器g(u,v)由统计误差函数的数学期望取最小值时得到

g(u,v)=argminE[|x(u,v)-x′(u,v)|2]

(11)

求解该最小值问题,得到滤波器g(u,v)的离散傅里叶变换G(ω,ξ)为

(12)

式中:H*(ω,ξ)为退化函数h(u,v)的离散傅里叶变换的复共轭;Sη(ω,ξ)为噪声的自功率谱;Sx(ω,ξ)为输入信号的自功率谱。

根据维纳滤波器G(ω,ξ)可以得到复原图像表示为

(13)

式中:F-1表示傅里叶逆变换;Y(ω,ξ)为退化图像y(u,v)的傅里叶变换。

3 人眼像差分析和泽尼克多项式表示

人眼可以看做一个结构复杂的光学系统,如图4所示,光学现象及定律在人眼中同样适用。人眼屈光在不同部位存在不同程度的缺陷导致点光源在视网膜上形成弥散斑,不能完全聚焦于一点,因此会出现不同程度的人眼波前像差。波阵面的位置会对波前像差的大小产生影响,并且它们之间存在某一函数关系。本文依据目前常用的由美国光学学会(OSA)提出的坐标系统[12],如图5所示。

图4 眼球结构图Fig.4 Eye structure

图5 人眼坐标系统Fig.5 Human eye coordinate system

(14)

使用前三阶像差进行人眼波前像差的计算,对于四阶及以上的像差忽略不计,得到用于眼底成像的波前编码光学系统的广义光瞳函数为

(15)

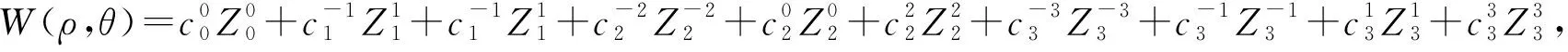
表1 人眼波前像差对应的Zernike多项式系数Tab.1 The Zernike polynomial coefficient corresponding to human echoes

4 基于波前编码技术的眼底成像结构设计及其图像处理

在视网膜成像系统的出瞳位置添加一块相位分布为Z=α·(x3+y3)的三次相位板,对眼底的图像进行编码,并在后期使用反卷积解码算法获取清晰视网膜图像。该系统可以大大简化传统眼底相机系统的复杂光学结构,同时也具有修正人眼的高阶像差的作用。

整个眼底相机系统是基于间接眼检镜结构而设计,前物镜位于距眼球5～50 mm的工作距离处,该镜头具有同时传递照明光线到眼底、收集眼底的反射光以及提供一个放大的眼底观测视角的作用。本文设计了一个基于这种成像原理的眼底仿真成像模型,该模型由眼底成像光路和眼底照明光路组成,其结构如图6所示。

在设计的仿真成像模型中,三次相位板的面型为Z=α·(x3+y3)(α=90.109 6)[17-18],并位于系统的出瞳位置,可以改变整个系统的出瞳函数。眼底相机使用LED作为系统的照明光源,该照明光束通过一个不透光的环形掩膜后形成环形照明图案,然后通过聚光镜汇聚入射到分光镜,经过分光镜反射通过物镜聚焦到眼球角膜表面。这种近朗伯照明模式,可以减少角膜的反射,获得适合光照的眼底图像视野。由视网膜反射发出的成像光路由CCD照相机收集,其中在眼球和出瞳位置之间设计了一组4f信息处理系统,L1、L2分别是4f系统的第一、第二傅里叶变换透镜,P为频谱面,在频谱面中设置不同相位板模拟不同个体的眼球像差。

图6 眼底相机系统结构示意图Fig.6 Fundus camera system

在基于波前编码技术的眼底仿真成像模型中,系统的PSF根据系统的出瞳函数Q(x,y,W(ρ,θ))计算得到

h(x′,y′)=κ{F[Q(x,y,W(ρ,θ))]}{F*[Q(x,y,W(ρ,θ))]}

(16)

式中:W(ρ,θ)表示人眼像差;*表示复共轭;F是傅里叶变换;κ是归一化参数。

在4f信息处理系统的频谱面P处引入人眼波前像差W(ρ,θ),出瞳位置添加三次相位板改变出瞳相位,由式(15)计算眼底成像系统的出瞳函数Q(x,y,W(ρ,θ)),代入式(16)得到由人眼像差和相位板共同组成的系统PSF,用MATLAB软件仿真模拟得到基于三次相位板的眼底成像模型的PSF如图7所示。

图7 点扩散函数Fig.7 Point spread function

人眼像差中除了离焦外还有彗差、像散、球差等初级像差,其PSF呈两条不规则圆弧形向外扩散(图7(a)、图7(d)),使用三次相位板改变波像差后的波前编码PSF(图7(c)、图7(f))仍保持了三次相位板PSF的基本直角三角形状(图7(b)、图7(e)),因此可以用来对人眼像差进行校正。

视网膜曲面通过光学系统的成像过程可以用离散二维卷积加上噪声的模型模拟表示,其计算过程为

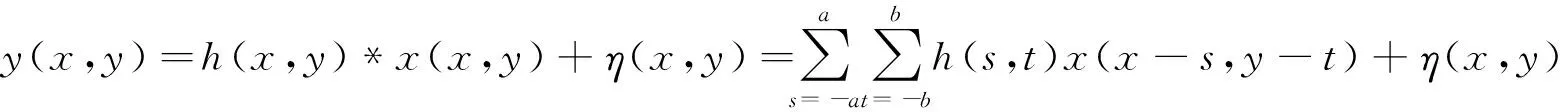
(17)

式中:*表示卷积计算;y(x,y)表示像面图像;x(x,y)表示物平面上的点;h(x,y)表示成像系统的点扩散函数(PSF);η(x,y)表示成像过程中引入的噪声;a和b表示点扩散函数的尺度大小。

利用DRIVE数据集[19]作为测试图片验证基于三次相位板的眼底成像模型,图像尺寸为584×565像素,成像过程中的PSF由式(16)计算得到,且选取中心21×21像素作为卷积核,同时引入信噪比为50 dB的高斯白噪声模拟成像过程中噪声的干扰。在得到由相位板编码的眼底模糊中间图像后,通过相位板已知的点扩散函数形式,设置估计的信噪比参数为0.1,利用维纳滤波算法可以得到清晰的眼底图像,结果如图8所示。

图8 基于三次相位板的眼底成像Fig.8 The fundus images based on the cubic phase plate

图8(a)为眼底原图像,图8(b)为经过三次相位板编码以及加入噪声后的模拟成像结果,图8(c)为经过反卷积复原的高对比度清晰眼底图像。结果表明本系统不用测量和补偿人眼像差,只需在成像系统的出瞳位置添加一块三次面型的相位板对图像进行编码,并在后期利用相位板的点扩散函数进行反卷积复原,就能得到高对比度的眼底图像。

不同的个体由于瞳孔直径、屈光能力等因素的差异,眼球的像差也会有不同幅度的变化,因此,为了评估基于波前编码技术的眼底成像系统对不同个体的眼底成像质量,对模型中表示眼球像差的Zernike多项式引入均值为0,标准差为0.1的高斯随机变量,则不同个体的人眼像差在原像差式(14)的基础上增加高斯随机变量后,得到

(18)

式中Gaussian(μ,σ2)表示均值为μ,标准差为σ的高斯随机分布变量。

不同个体成像时的系统PSF和眼底图像仿真结果如图9和图10所示。

图9 不同人眼像差情况下的点扩散函数Fig.9 Point spread functions with different eye’s aberrations

由图9可以发现,不同个体的人眼像差PSF存在差异,而在出瞳位置添加三次相位板的系统PSF则基本保持一致,这也说明了三次相位板对不同个体的人眼像差的补偿和校正具有较好的鲁棒性。图10(a)是不同个体的眼底成像仿真实验原图,将图9(b)表示的由三次相位板校正后的不同个体人眼像差PSF带入眼底成像模型式(17)中,同时引入50 dB的噪声,可以得到如图10(b)所示的中间模糊图像。使用维纳滤波算法对中间模糊图像复原,算法中的估计PSF选取单独的三次相位板PSF(如图7(b)所示),估计信噪比参数取值为0.1,最终得到如图10(c)所示的清晰眼底图像。图10的仿真成像结果表明本文设计的三次相位板眼底成像系统针对不同个体的人眼像差,采用三次相位板编码后,用维纳滤波均能复原出清晰的眼底图像。

图10 不同个体像差的眼底成像仿真图像Fig.10 Simulation images of different individual aberrations fundus

5 结 论

本文分析并验证了波前编码技术在眼底成像系统应用的可行性。在眼底成像系统中引入具有波前编码功能的特定相位板,可以对眼底图像进行编码,使图像对像差不敏感,再通过后期的反卷积复原,得到具有高分辨率的眼底图像。通过实验仿真,验证了采用三次相位板实现图像编码,并通过经典维纳滤波算法进行图像反卷积,可以获得高对比度的眼底图像。实验结果表明,将三次相位板应用于眼底成像系统,可以在眼底成像过程避免对人眼像差的检测和补偿,从而有效降低系统的复杂性和成本。