中国地方政府债务风险指数研究

闫 衍 王新策 袁海霞

内容提要：随着2014年新《预算法》、国发43号文等相关地方债务风险防范政策的出台，我国地方债务管理机制的不断完善，地方政府显性债务风险总体可控，但隐性债务剧增以及部分地区负债水平过高带来的结构性风险和区域性风险仍需关注。在这种背景下，有必要构建债务风险指数对全国地方债务风险情况和风险变化趋势进行监测，以起到风险预警的作用。本文首先就各种风险评价方法进行了分析和比较，在此基础上选择AHP方法来构造我国地方债务风险指数模型。再对AHP方法进行了梳理和优化，得到基于AHP方法的风险指数模型。最后用该模型分别对2016年我国省级地方政府和重庆市区县地方政府债务风险指数进行估算。从结果来看，该模型能够客观地反映各级地方政府债务风险情况，并验证了由于隐性债务剧增导致整体风险显著增加的结果。

引 言

1994年分税制改革后，中央收回了部分财权，但地方政府承担着大量经济建设等事权，财权与事权不匹配加剧了地方财政收支矛盾。另一方面，受到《预算法》的约束，地方政府无法通过自主发债进行融资。在此背景下，“融资平台”应运而生。地方政府成立各类城市投资公司作为融资平台，以此代替地方政府进行直接或间接融资，以弥补资金缺口。与此同时，以GDP为主导的绩效考核机制与政府竞争模式，促使地方政府发展重规模轻质量的投资模式，粗放型的财政支出行为导致了地方融资平台的快速生长。2008年金融危机后，在“四万亿”政策的推动下，截至2010年底，债务余额达到4.97万亿，债务风险初步显现。2011年后，地方融资平台依托影子银行，债务规模进一步扩张。截至2013年6月底，债务余额达到6.79万亿，急剧攀升的地方政府债务也为金融体系带来了潜在隐患。2014年，政府通过颁布新《预算法》与《国务院关于加强地方政府债务管理的意见》（简称43号文），对地方债务进行规范化的监督和管理。

自我国经济进入新常态以来，经济增速稳中趋缓，以“防风险”为基础的“促改革”持续推进。中央经济工作会议提出将防范化解重大风险列为2018年三大攻坚战之首。4月2日，中央财经委员会第一次会议首次提出“结构性去杠杆”，为“打好防范化解重大风险攻坚战”划定基本思路。2018年一季度以来，财政部及相关部门围绕防范地方债务风险密集出台多项政策，一方面延续了《预算法》与43号文的“开前门，堵后门”的监管框架，另一方面做好进一步纵深细化工作，对各类违法违规举债行为“围追堵截”，明确未来地方债务管理及改革思路，也体现了中央对地方债务问题的重视和监管决心。随着相关防范政策密集出台和管理机制不断完善，地方政府显性债务增幅有所趋缓。据中诚信测算，2017年我国地方政府显性债务规模约为16.47万亿①根据全国各省份财政决算报告及中诚信国际测算。，风险总体可控，负债率为36.2%，低于欧盟60%的警戒线；但隐性债务持续恶化，地方政府通过PPP项目、政府购买服务、资管计划、明股实债等方式变相举债造成的隐性债务风险问题尤其突出。2017年我国地方政府整体隐性债务规模在26.5万亿-35.9万亿之间，约为显性债务的1.6-2.2倍，考虑隐性债务的负债率直接上升至68%-80%，高于欧盟60%警戒线。其中，区域性债务风险分化严重，负债率超过60%警戒线的省市自治区依次为贵州、北京、青海、天津等；债务率方面，除海南、西藏以外，其余29个省市自治区均超过100%警戒线。根据上述测算，我国地方政府债务风险总体可控，但隐性债务剧增以及部分地区负债水平过高带来的结构性风险和区域性风险仍需关注。因此，构造地方政府债务区域风险指数十分必要，通过该指数准确监测全国各地区地方政府债务风险情况和风险变化趋势，以便在危机初期及时采取防范措施控制债务风险的加剧和扩散。

一、方法综述与研究

自20世纪80年代以来，随着全球各国政府债务积累的日益严重，国外学者开始研究政府债务风险问题。早期研究主要以地方政府财政和债务的数据为基础，构造系统的指标体系③Ma J.，Monitoring Fiscal Risks of Subnational Governments：Selected Country Experiences，Oxford：Oxford University Press，2003.③Charle S.，Measuring and Forecasting Debt Capacity State of Oregon Experience.Government Finance Review，2008（12）：44-74.，用于检测债务风险的变化趋势。预警指标包括债务负担率、偿债率、逾期率、债务依存度、担保债务比重等。在借鉴国外研究成果的基础上，结合我国特有的政治体制、历史背景，国内学者建立了符合我国国情的地方政府债务风险模型，包括基于新增债务的动态风险预警模型④刘尚希、赵全厚：《政府债务：风险状况的初步分析》，《管理世界》，2002（5）：22-32。，合成指数与层次分析法相结合的风险预警模型⑤裴育、欧阳华生：《我国地方政府债务风险预警理论分析》，《中国软科学》，2007（3）：110-114。等线性组合方法。最近几年，随着大数据、云计算和智能算法的普及，国内专家学者也开始通过数学统计模型和机器学习算法实现地方政府债务风险的测算和预警，并取得了丰硕的成果，其中包括基于因子分析法的风险评估预警系统、粗糙集理论与BP神经网络结合的风险预警系统、基于改进后的模糊评价分析法、灰色关联法与BP神经网络相结合的风险指数模型，以及基于KMV模型的风险预警指数等。

地方政府债务风险指数模型的构造思路是结合地方政府的宏观经济、财政实力和债务水平等情况给出地方政府债务一个定量的风险综合评价值，模型的核心是评价方法。综合上述已有研究成果和一些经典的评价方法，根据各评价方法所依据的理论，将它们分为五大类：

（一）指标评价方法

指标评价法，是出现较早的一种评价方法，它根据专家分析和历史经验选择与风险最相关的单指标（或多指标的简单线性组合）来评价风险。

（二）数学模型评价方法

层次分析法（Analytic Hierarchy Process，AHP），是由T.L.Saaty①T.L.Saaty，The Analytical Hierarchy Process.McGraw-Hill，1980.提出，一种定性与定量分析相结合的多层次结构模型。它是一种系统性的分析评价方法，通过分解、判断和综合的思维过程处理决策问题，既包含了主观的逻辑判断和分析（定性），又依靠客观的精确计算和推演（定量）。

模糊综合评判法（Fuzzy Comprehensive Evaluation，FCE），是由 L.A.Zadeh②L.A.Zadeh，Fuzzy Sets，Information and Control，1965，8：338-353.提出，它是以模糊数学为基础，应用模糊关系合成的原理，将一些边界不清、不易定量的因素定量化的一种综合评价方法。

数据包络分析法（Data Envelopment Analysis，DEA），是由 A.Charnes和 W.W.Coope③A.Charnes，W.W.Cooper and E.Rhodes，Measuring the Efficiency of Decision-Making Units，European Journal of Operational Research，1978，2：429-444.等人提出，是以“相对效率”概念为基础，根据多项投入指标和多项产出指标，利用线性规划的方法，对具有可比性的同类型单位进行相对有效性评价的一种数量分析方法。

（三）基于统计的评价方法

TOPSIS法（Technique for Order Preference by Similarity to an Ideal Solution），是由 C.L.Hwang和 K.Yoon④C.L.Hwang and K.Yoon，Multiple Attributes Decision Making Methods and Applications，Springer，Berlin，1981.提出，根据有限个评价对象与理想化目标的接近程度进行排序的方法，是在现有的对象中进行相对优劣的评价。

主成分分析法（Principal Components Analysis，PCA），是由 Karl Pearson⑤Pearson K.，On Lines and Planes of Closest Fit to Systems of Points in Space，Philosophical Magazine，1901，2（11）：559-572.提出，利用降维的思想，把多指标转化为少数几个综合指标（即主成分），其中每个主成分都能够反映原始变量的大部分信息，且所含信息互不重复，用来解决数据多重共线性问题。

（四）机器学习等新型评价方法

人工神经网络（Artificial Neural Network，ANN），是模拟生物神经网络进行信息处理的一种数学模型，通过模拟大脑的学习机制实现对数据的预测或分类。所谓“学习”就是神经网络系统受到外界刺激下调节自身系统以适应新环境的一个过程。从数学模型而言，就是通过不断的训练样本（学习），调节模型参数使系统输出更接近样本输出（误差更小）的过程。

灰色综合评价法（Grey Comprehensive Evaluation，GCE），是由邓聚龙⑥JL Deng，Control Problems of Grey Systems，Syst Control Lett，1982，1：288-294.提出，一种以灰色关联分析理论为指导，基于专家评判的综合性评价方法。

（五）组合评价方法

组合方法是将上述几种方法组合使用的情况。每种方法都有自身的优点和缺点，其适用场合也并不完全相同，通过将具有同种性质的综合评价方法组合在一起，就能够使各种方法的缺点得到弥补，同时又具有各方法的优点。

二、模型方法选择

本文将通过比较上述综合评价方法的主要优点、主要缺点和可行性前提，来选择合适的方法建立地方政府债务风险指数模型（见表1）。首先，地方政府债务风险指数是综合了地方政府经济、财政和债务等多维度指标的一个综合性评价值，简单的指标评价法无法实现这样的效果。其次，地方政府债务风险指数除了用来量化债务的风险程度，还能从中挖掘风险成因，从而指导对债务风险的控制。PCA法对原数据进行降维，降维后的主成分指标是没有可解释意义的，该方法不能用于对债务风险成因的解释。此外，当前比较流行的人工神经网络等机器学习算法，其优秀的精确度是建立在大量的历史数据和反复迭代训练基础上的。而本次风险指数的估算并不属于第二次迭代过程，所以不适用。另外，DEA法无法解决数值为负的问题，而GDP增速等指标可能为负，因此该方法也无法适用。同时，组合方法是建立在多种评价方法的基础上，应该在多种评价模型完成后再考虑。最后，剩下的AHP、FCE、TOPSIS和GCE四种评价方法中，FCE、TOPSIS和GCE的可行性前提是事先给出权重，而AHP，通过元素间相互比较和定性转定量的方式给出权重，很好地解决了这一问题。换句话说，AHP是另外三种评价方法的基础，也是组合方法的基础。因此，应该优先考虑AHP来构造地方政府债务风险指数模型。

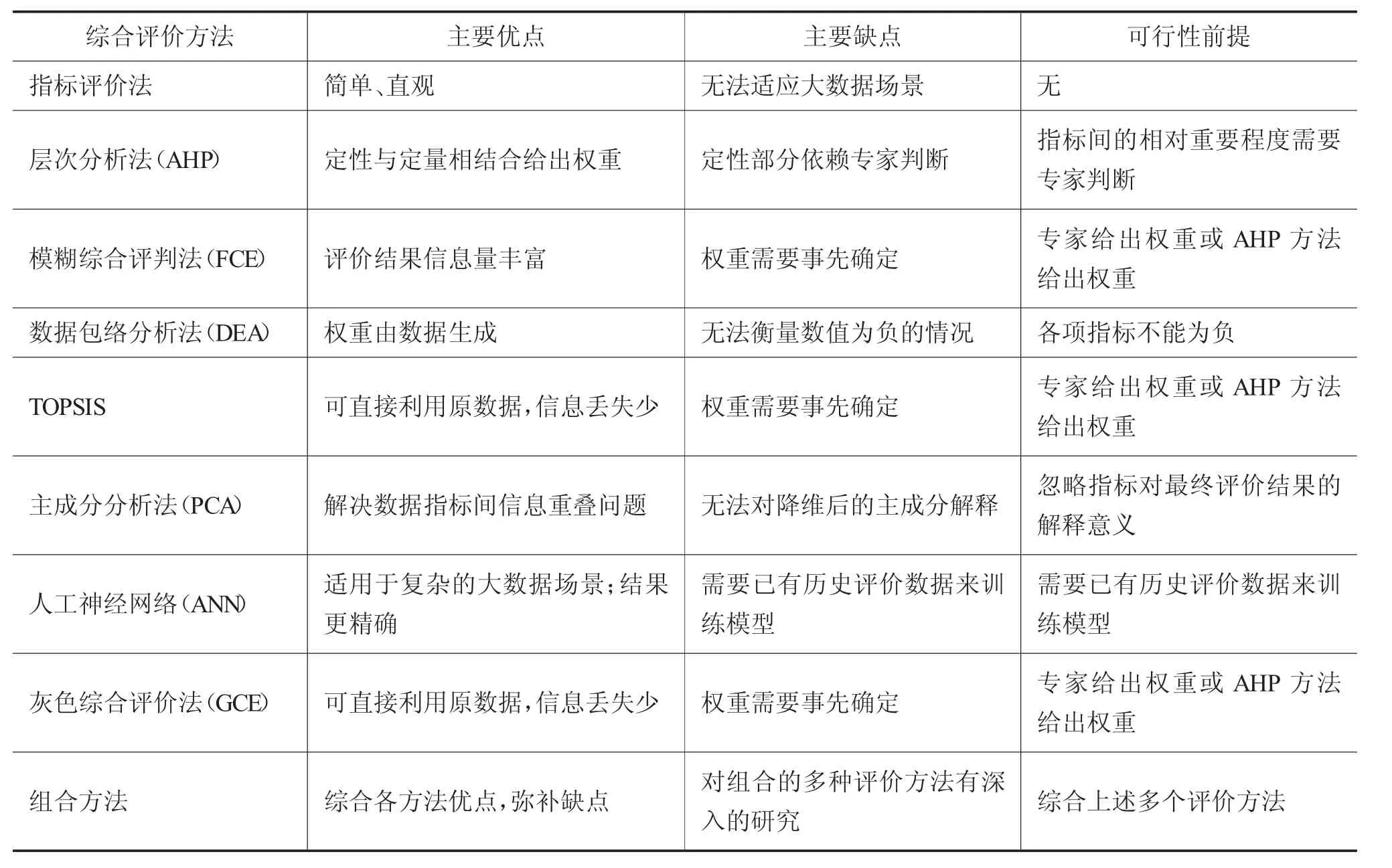
表1 综合评价方法比较

另外，由于AHP在处理各种复杂决策问题方面的实用性和有效性，在各个领域都受到了重视。它的应用遍及经济计划和管理、能源政策和分配、行为科学、军事指挥、运输、农业、教育、人才、医疗和环境等领域。该方法的学术研究也涉及核反应堆的选择、如何减少全球变暖的冲击、大学专业选择、检验软件系统的质量、海外制造工厂地点的选择和评估跨国石油管道经营风险等研究课题。总结上述AHP法适用的各类决策问题类型，地方政府债务风险指数所属的类型是相对排名问题（见表2）。AHP方法在该领域已经有许多成熟的应用，类似问题包括大学专业选择、高校排名等。因此，AHP方法构造地方政府债务风险指数模型具备适用性和可行性。

表2 AHP适用的决策问题类型

三、AHP方法基本原理与优化

AHP方法是一种定性和定量相结合的、系统化、层次化的分析方法。对于复杂的决策问题，AHP把总目标分为多个子目标，按总目标到各层子目标的逻辑顺序将整个决策系统自上而下分解成一个树状结构，从而形成一个有序的递阶层次系统；通过指标间相对比较关系进行模糊定性量化，构造判断矩阵，求得每一层各个指标对上一层目标的权重向量；最后对所有子目标问题进行汇总，采用加权和的方法逐阶层归并获得总目标的最终权重向量，得到最底层每个指标对于最上层总目标的影响权重，并计算出总目标的最终评价结果。下面仅以三层结构模型为例解释AHP方法的基本原理。

步骤一：建立层次结构模型

AHP方法处理系统的决策问题，首先要确定总目标和影响总目标的所有元素，再给出其结构模型。其层次结构如图1，根据其性质可以分为三类：最高层（目标层），是决策问题的总目标，只包含一个元素O；中间层（准则层，可以包含多个准则层），是为了实现总目标所涉及的各子目标，有子目标 C1…Cn；最底层（方案层），是实现各决策目标的方案，即影响元素，P1…Pm。

步骤二：构造各层次的判断矩阵

图1 三层递阶层次结构

接下来需要确定每一层元素对于上一层作用关系元素的影响程度，即对于每个目标元素，其支配下层的元素应该分配多少权重，这里将通过判断矩阵来计算具体权重。判断矩阵通过该层所有元素之间两两相对重要程度比较来获得，具体采用1-9标度方法（见表3）。

表3 AHP方法1-9相对标度

最高层与中间层的判断矩阵，将元素C1…Cn进行两两相对比较，根据表3相对标度得到判断矩阵A。矩阵A对角线的元素为每个元素与自身相比较，结果为同样重要，标度值为1。

步骤三：计算各层次权重向量

通过求出矩阵A的最大特征根λmax以及其对应的特征向量W*，对W*归一化处理后就能获得权重向量W=（w1，w2，…，wn）T。比较普遍的近似解法有根法、和法和幂法。根法对判断矩阵每行几何平均数处理，归一化后得到权重向量；和法先对判断矩阵按列归一化，再按行求和，最后进行归一化得到权重向量；幂法是一种逐步迭代的方法，对任意一组初始向量用判断矩阵进行重复映射，直到结果满足一定的精确检验为止，最后构造出权重向量。三种方法相比较，幂法的迭代过程相对繁琐，根法相对和法的计算步骤简洁，因此我们选择了根法。

根法计算步骤：

（4）计算 λmax的值，

步骤四：一致性检验与调整

所谓一致性是指判断思维的逻辑一致性，如甲比丙重要得多，乙比丙稍微重要，则甲一定比乙重要。而对元素进行两两比较是一个主观过程，很容易产生逻辑一致性的矛盾，因此需要一致性检验。矩阵一致性的数学定义是：

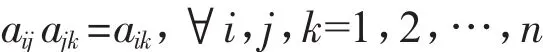
通过引入两个指标来检验判断矩阵的一致性程度，这两个指标分别是一致性指标CI（Consistency Index）和一致性比率 CR（Consistency Ratio）：

这里的平均随机一致性RI（Random Index）是多次重复进行随机判断矩阵特征值的计算后取算术平均数得到的。在一致性检验中，CI越大矩阵A的不一致程度越严重，CI=0矩阵A完全一致。CR是用来检验可靠性的一致性检验指标，当CR＜0.1，认为判断矩阵一致性可以接受；否则需要调整判断矩阵中的值直到通过一致性检验为止。

步骤五：加权汇总结果

对第一层与第二层的权重W=（w1，w2，…，wn）T和第二层所有子目标Ci与其支配的第三层元素的权重为 Vi=（vi1，vi2，…，vim）T，i=1，2，…，n 进行线性加总，得到最终总目标 O 的评价估值：

底层元素（P1，P2，…，Pm）T对于总目标 O 所分配的最终权重为（u1，u2，…，um）T，这里（P1，P2，…，Pm）T的值是经过归一化处理后的值。

优化步骤：消除多重共线性

事实上，无论是AHP还是FCE、TOPSIS和GCE，都无法解决变量多重共线性问题。虽然PCA能很好地解决这一问题，但其降维后的主成分指标不能给具有实际意义的解释（主成分空有信息而无实际含义），这样就无法从风险指数中挖掘其债务风险的成因。为了解决AHP法多重共线性问题，我们先采用皮尔逊相关系数来测算数据指标间的相关系数矩阵，再根据结果和一定筛除原则对其中高线性相关指标进行剔除。

对于两个连续变量（x1，x2，…，xn）和（y1，y2，…，yn）其 Pearson 相关系数计算公式为：

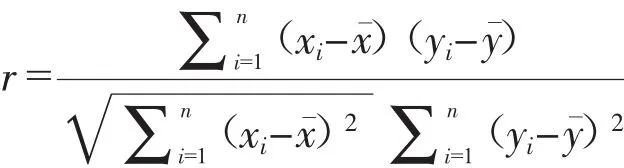
相关系数r的取值范围表示存在不同程度线性关系：

具体的优化过程，首先计算所有底层元素（P1，P2，…，Pm）T相关系数矩阵r（iji，j=1，2，…，m）。对计算结果中高度线性相关的指标集｛0.8＜rij＜1｝进行分析和筛选，以消除指标间信息重叠问题。筛除原则：（1）优先考虑支配更多高度线性相关指标的子目标Cx，删除该子目标Cx支配下高度线性相关指标中与其他指标系数相对值高的指标（例如高度线性相关指标i，j属于Cs，k属于Ct，则先删除（2）对于不同子目标下的高度线性相关指标，综合数值和分属子目标的实际意义进行删减。

优化版AHP方法的步骤流程图（见图2）。

图2 优化版AHP逻辑流程

四、中国地方政府债务风险指数实证分析

按照图2优化版AHP逻辑流程的思路，构建地方政府债务风险指数模型。

（一）样本指标提取与筛选（消除指标多重共线性）

本次模型提取的样本指标：GDP、GDP增长率、人均GDP、税收收入占比、财政平衡率、综合财力、财政收入、政府债务余额、债务率和负债率。

为了对指标进行多重共性的测算和筛除，下面给出四组结果包括省级地方政府（不含隐性）债务指标、省级地方政府（含隐性）债务指标、重庆区县（不含隐性）债务指标和重庆区县（含隐性）债务指标。

图3-1 省级地方债务（不含隐性）指标相关系数矩阵

图3-2 省级地方债务（含隐性）指标相关系数矩阵

图3-1与图3-2中的GDP、财政收入和综合财力之间的相关系数都超过0.9；图3-3中的GDP、综合财力、一般公共预算收入和显性债务之间的相关系数超过0.8，其中GDP与一般公共预算收入的相关系数甚至超过0.9；图3-4中的GDP、综合财力、一般公共预算收入之间的相关系数超过0.8，其中GDP与一般公共预算收入的相关系数甚至超过0.9。显然，在这几个高度显性相关指标中，GDP与其余几个指标的相关系数最高，可以剔除。

（二）建立层次结构

下面构造省级地方政府债务（不含隐性）风险指数模型。对指标进行分类，可以得到宏观经济、财政实力和债务水平三类指标，从而得到递阶层次结构（见图4）。

（三）判断矩阵与权重计算

根据中诚信国际研究院团队的分析，完成了对图4中所有判断矩阵的估算。再运用Python和R对上述判断矩阵进行近似解法（根法）求得权重向量并通过一致性检验，结果如表4所示。

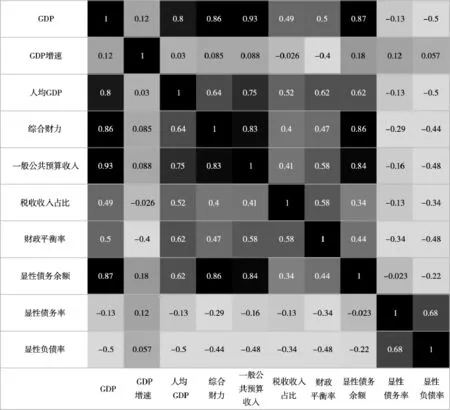
图3-3 重庆区县地方债务（不含隐性）指标相关系数矩阵

（四）加权汇总

根据表4结果汇总得风险指数公式：

其中，Z是风险指数，（X1，X2，…，X9）分别是GDP增长率等9个指标归一化的指标值。由于宏观经济和财政实力对债务风险指标起正面作用，而债务水平指标对债务风险起负面影响，因此，宏观经济和财政实力前面符号为正，债务水平的为负。

风险指数Z取值范围为［-0.258，0.742］，区间的左端点表示风险最大边界，其含义是，没有任何经济和财政收入能力但债务水平最高；区间的右端点表示风险最小值的边界，其含义是，经济和财政情况最好而且没有任何债务。为了实现风险指数越大债务风险越大的实际含义，通过映射函数Z′=-Z+0.742得到最终风险指数公式：

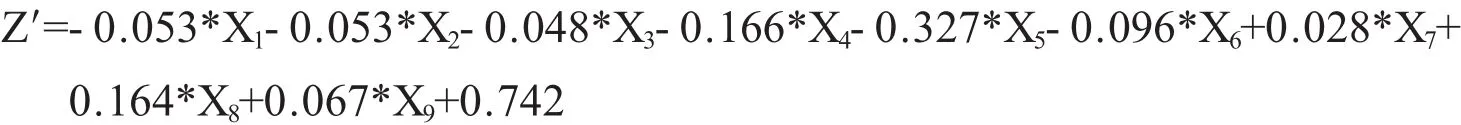
图3-4 重庆区县地方债务（含隐性）指标相关系数矩阵

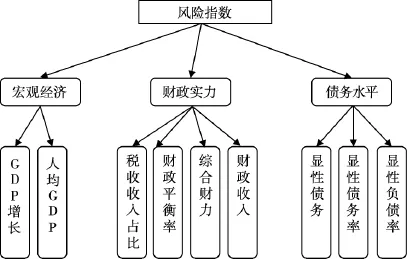
图4 省级地方政府债务（不含隐性）层次结构

表4 权重向量与一致性检验结果

实例结果与分析

2016年我国省级地方政府债务风险指数结果如下：

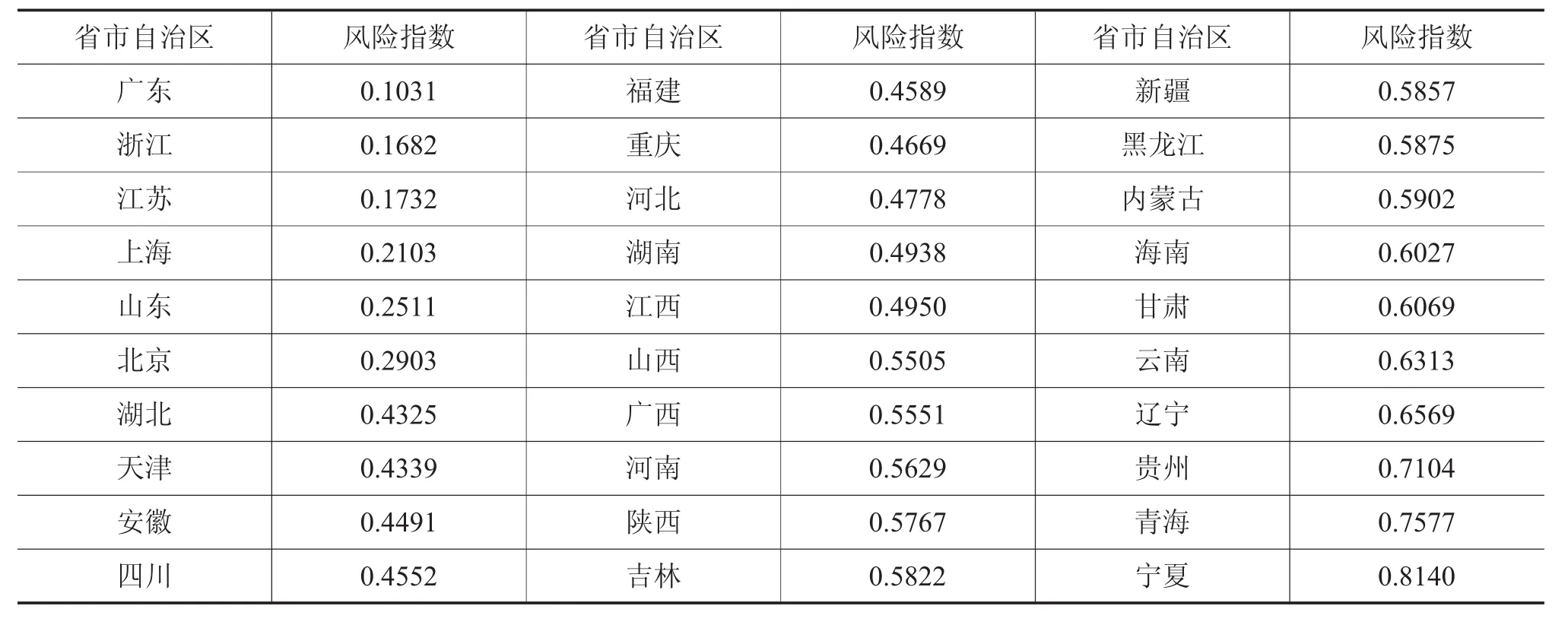
表5-1 2016年省级地方政府债务（不含隐性）风险指数

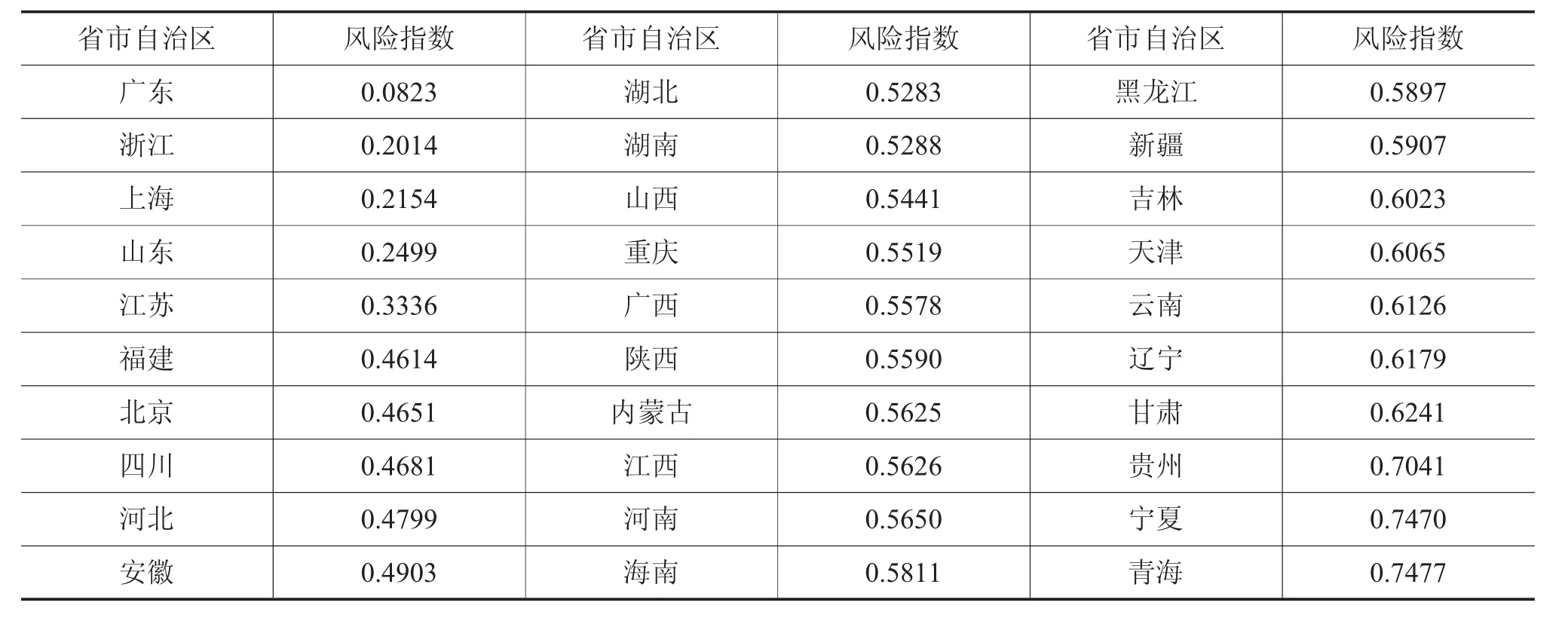
表5-2 2016年省级地方政府债务（含隐性）风险指数

从表5-1和表5-2的结果来看，债务风险指数高低的整体分布和地区的财政实力有关。风险指数最低的前几个省份是财政实力最强的广东、浙江、江苏、上海、山东和北京，而风险指数最高的是中西部财政实力较弱的省份。整体而言，依次从长三角、珠三角等东部沿海省份到中西部、东北三省，债务风险指数逐步上升。具体来看，综合财力的正面影响效应最大，财政收入和人均GDP次之。我国各省份的GDP增速、税收收入占比和财政平衡率的数值差异性较小，这些指标对最终指数结果影响不大。此外，债务规模对经济较差的省份负面影响较大。例如，负债率最高的贵州、青海、云南、辽宁和宁夏刚好也是风险指数最高的几个省份。债务率对经济较差的省份也有负面放大效应。债务余额方面，该指标与地区的经济发展程度高度正相关，即经济发展程度和负债规模是成正比的。但贵州和辽宁有着与它们经济能力不匹配的债务余额，导致它们处于重度债务风险区间。

比较不含隐性债务与含隐性债务的指数结果，其中变化最大的依次是北京、天津、江苏、湖北和重庆。具体来看，债务率（隐性）和负债率（隐性）最高的省份同为北京、天津和江苏，它们的隐性债务是显性债务的3倍以上，远远高于其他省份。隐性债务剧增导致天津跌入风险重灾区，而北京和江苏的风险指数因此有明显变化，分别增长了58%和94%。湖北和重庆的情况也不容乐观，隐性债务比显性债务增加了2倍左右，排名也明显下降。

最后，整体比较不含隐性债务和含隐性债务风险指数分布结果，计算两个结果风险指数的平均值和方差，前者的为0.45和0.31，后者的为0.51和0.24，隐性债务使各省份整体平均风险指数明显增加，同时各省的风险差异性变小。从图5可观察到增加隐性债务后的风险指数分布明显后移，并有向中间聚集的趋势。表明整体的风险明显上升，同时风险分布向中间集中。

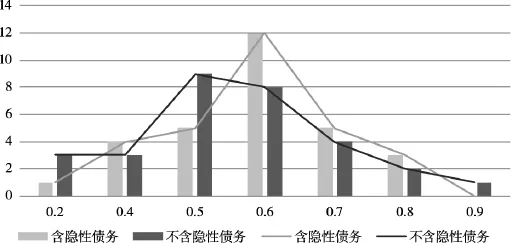
图5 2016年省级地方政府债务风险指数分布

2016年重庆市区县地方政府债务风险指数结果见表6-1、表6-2。

从表6-1和表6-2来分析2016年重庆市区县地方政府债务风险指数，其结果和省级地方政府风险指数结果一致，综合财力、人均GDP和财政收入几乎决定了该风险指数的整体分布。GDP增长率、税收收入占比和财政平衡率因为数值差异较小对结果影响不大。此外，负债率和债务率对经济较差地区的负面效应有放大效果。地区的债务余额如果和经济实力不匹配则会加大其债务风险。

隐性债务方面，增加隐性债务后几乎所有区县的债务率将近翻了一番。其中最严重的是沙坪坝区，债务率由0.6直接增长到6.1，其风险指数排名从第六直接降到中游位置，类似情况的还包括合川区和重庆经济技术开发区。

最后，整体比较不含隐性债务和含隐性债务风险指数分布结果，从图6可观察到增加隐性债务后的重庆市各区县的整体风险明显上升了，风险指数的平均值从0.49增至0.53。

表6-1 2016年重庆市区县地方政府债务（不含隐性）风险指数

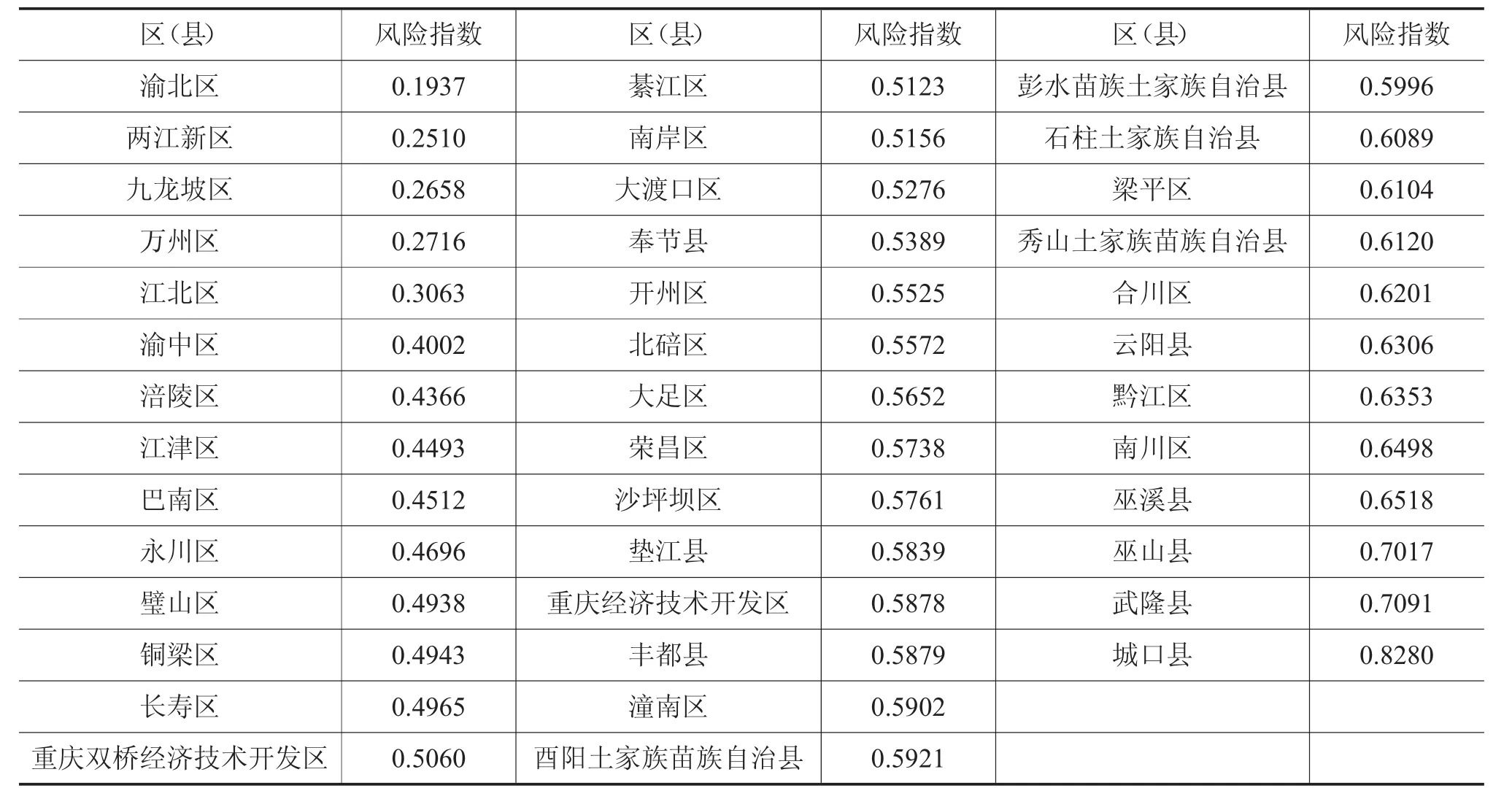
表6-2 重庆市区县政府债务（含隐性）风险指数

五、结 论

本文通过学习研究各种综合评价方法，比较并评估它们之间的优缺点、可行性前提和适用性场景，最后选择AHP方法来构造我国地方政府债务风险指数模型。通过梳理AHP方法的理论，结合风险指数的实际应用情况，对该方法进行了一定的优化。最后在此基础上，对2016年我国省级地方政府和重庆区县的地方政府债务风险指数进行估算。结论如下：

图6 2016年重庆区县地方政府债务风险指数分布

（1）地区的财政实力几乎决定其风险指数的分布位置。具体而言，综合财力对最终结果具有最强正相关性，财政收入和人均GDP次之，GDP增长率、财政平衡率和税收收入占比因数值的区分度不高对最终结果影响甚微。债务规模指标方面，负债率和债务率对经济较差地区的负面效应有放大效果。这和指标的构造有关，负债率和债务率的分母是GDP和综合财力，而经济较差地区的GDP和综合财力一般较差，导致这两个指标值较大。债务余额一般与地区的经济有一定相关性，如果地区的债务余额不能与其经济发展相匹配，则会加大该地区的债务风险。

（2）无论是省级地方政府债务还是重庆区县地方政府债务，隐性债务导致风险加剧的问题十分明显。加上隐性债务后，各地方政府整体的债务风险指数明显增加。省级地方政府债务风险指数的平均值从0.45增至0.51，重庆方面的平均值则从0.49增至0.53。局部情况则分化更加显著，省级地方政府方面，情况最严重是北京、天津和江苏，其隐性债务是显性债务的3倍以上，直接导致它们的风险指数增长了50%-90%，排名显著下滑。情况次之的湖北和重庆排名也明显下降。重庆区县方面，情况最严重的是沙坪坝区，债务率增长了10倍，风险指数增长65%，排名从第六跌至中游。类似的情况还有合川区和重庆经济技术开发区。

（3）基于AHP方法的地方政府债务风险指数能够很好地反映我国省级和市区县级地方政府债务风险情况，具有很好的参考价值。同时，通过该风险指数排名次序，我们能够从数据指标层面对风险成因进行进一步的深度挖掘分析，具有一定的研究价值。另外，优化方案把GDP指标剔除了，该指标反映的是地区的综合经济发展程度。在实例分析中发现，该指标与综合财力、财政收入和债务余额有一定的信息重叠，可以互相解释。因此，优化方案具有良好的实用价值。最后，该方法也为以后通过FCE、DEA和TOPSIS等综合评价方法构建地方债务风险指数模型提供了可行性前提。