基于NTSM的伺服电机模糊滑模控制策略研究*

黄 皓，涂群章，潘 明，蒋成明，薛金红，李 沛

(陆军工程大学 野战工程学院，江苏 南京210007)

0 引言

永磁同步电机(Permanent Magnet Synchronous Motor，PMSM)以其空间布置方便、输出功率大、控制精度较高等优点被广泛运用于智能机器人、新能源汽车和工业化无人机等领域。由于PMSM为非线性、多变量、强耦合性的复杂对象[1-3]，工业中一般采用常规的PID控制算法进行实时控制，常规的PID控制策略在控制过程中一般会存在启动速度慢、调节能力弱、抗干扰性差等缺点。为了实现永磁同步电机高效率、高精密度的控制，国内外学者针对不同的电机控制系统提出了诸如神经网络控制[4]、弱磁控制[5]、自适应控制[6-7]、滑模变结构控制(Sliding Mode Variable Structure Control，SMC)[8-10]等控制策略。其中SMC控制策略[11]由于具有对模型的参数变化不敏感、抗干扰性较好、鲁棒性强等优点被国内外学者予以重视。文献[12]提出了基于滑动模态的自适应扰动补偿器的设计，解决了小惯量永磁同步电机的高精度调速控制问题。文献[13]通过在变结构控制的基础上设计了速度观测反馈系统，减少了速度观测误差。文献[14]通过提出一种积分型SMC控制策略，有效地提升了电机控制系统的控制精度。文献[15]在传统SMC控制策略的基础上，设计了负载转矩观测器，较大程度减少了由于负载扰动造成的误差。文献[16]提出了一种自适应滑模控制策略，有效地提升了控制系统的动态性能。文献[17]设计了一种基于滑模变结构的永磁同步电机弱磁矢量控制策略，有效地提升了永磁同步电机在高速运转时的稳定性。

以上控制策略都有效地提高了电机控制系统的控制精度，但在控制过程中存在以下两点不足：第一，采用的都是线性滑模面，滑模系统的跟踪误差无法在有限时间内收敛为0；第二，传统SMC控制策略会产生较为严重的抖振现象，以上控制策略都没有针对减弱抖振采取有效措施。针对以上两点不足，本文设计了一种基于非线性Terminal系统的永磁同步电机Fuzzy-SMC控制算法。通过非线性Terminal滑模面代替传统SMC控制策略中的线性滑模面，解决跟踪误差收敛过慢问题。以削弱抖振现象为目的制定模糊规则，通过模糊控制器实时调整滑模控制增益实现削弱抖振现象。通过MATLAB/Simulink仿真和永磁同步电机台架测试试验验证了本文提出控制策略的有效性。

1 非线性Terminal滑模面设计

1.1 线性滑模面

在传统滑模控制中，国内外学者普遍采用线性滑模面进行控制，当控制系统中的运动点趋近滑模区域时，使得跟踪误差逐渐削减到零[18]，跟踪误差的收敛速度通过调整滑模面的控制参数来改变。线性滑模面控制式如下:

s=cx1+x2

(1)

式中，c>0，x1为跟踪误差，x2为跟踪误差对时间求导。

然而传统线性滑模面存在两点不足之处：第一，当运动点在滑模面上趋近滑模区域时，跟踪误差会不断削减，但无法在有限的时间内削减到0，这将影响永磁同步电机实现高精度的控制；第二，传统线性滑模面采用的为等速趋近率，等速趋近率自身存在缺点，即切换带为带状，当系统在切换带运动时，最后不能趋近于原点，而是原点产生抖振带，这种抖动可能激励系统中存在未建模高频成分，并可能增加控制器的负担[19-20]。

1.2 非奇异Terminal滑模面

非奇异终端滑模面(Nonsingular Terminal Sliding Mode，NTSM)在终端滑模(Terminal Sliding Mode,TSM)[21-22]的基础上发展而来，可以解决终端滑模面上由于控制输入无穷大时产生的奇异现象。针对二阶非线性系统：

(2)

其中x(t)=[x2(t),x2(t)]T；d(t)≤D(t)为外部扰动，D(t)为已知函数，f(x,t)为动力学方程，x2(t)为参考点位置。

参照文献[18]，采用TSM控制策略，则设计控制器为:

(F(x,t)+D(t)+η)sgn(s))

(3)

式中:β、α为控制参数且大于0，sgn(s)为符号函数，F(x,t)为动力学方程f(x,t)的积分，λ为设计参数且λ>0,η为设计常数且η>0。

由等式(3)可得，控制策略中包含x1α/β-1x2，当x2≠0,x1=0时存在奇异区域，会使得设计控制器的值u(t)趋向+∞，此时控制器的设计没意义。

NTSM为解决奇异性问题，滑模面设计为：

(4)

根据等式(4),此时的控制器输出为

(5)

由式(5)可以看出，当x2≠0,x1=0，采用NTSM控制策略时，控制器输出不会趋于+∞，可以有效解决该二阶系统采用TSM控制策略时出现的奇异现象。

1.3 二阶离散系统例证

为了验证本文提出的NTSM控制策略的有效性，通过一个典型二阶离散系统基于MATLAB/Simulink进行仿真验证，该二阶离散系统如下式：

(6)

分析图1(a)和图2(a)可得，在两种滑模面的控制下本文所设计的典型二阶离散系统都具有较平稳的滑模运动相轨迹，控制过程中无明显的抖动，体现了SMC控制策略在控制过程中具有较好的平稳性。分析图1(b)和图2(b)可得，采用线性滑模面时，控制系统到达平衡点的趋近时间约为0.61 s，而采用NTSM滑模面控制时的趋近时间约为0.16 s，趋近速度提升了70%以上，同时图2(b)也可证明本文提出控制策略趋近过程中系统收敛性优良。分析图1(c)和图2(c)可得，采用线性滑模面进行控制时，控制器输出u到达平衡点所用时间约为1.28 s，而采用NTSM滑模面对二阶离散系统进行控制时所用时间约为0.78 s，由此可见本文设计的NTSM滑模面相较传统线性滑模面达到稳态的速度更快。分析图(d)和图2(d)，采用线性滑模面进行控制时完成阶跃响应所用时长约为1.58 s，而采用NTSM滑模面进行控制完成阶跃响应所用时长为1.18 s，由此可见，通过采用本文的NTSM滑模面对二阶离散系统进行实时控制时可比传统线性滑模面提升20%以上的响应速度。

图1 基于线性滑模面系统仿真曲线

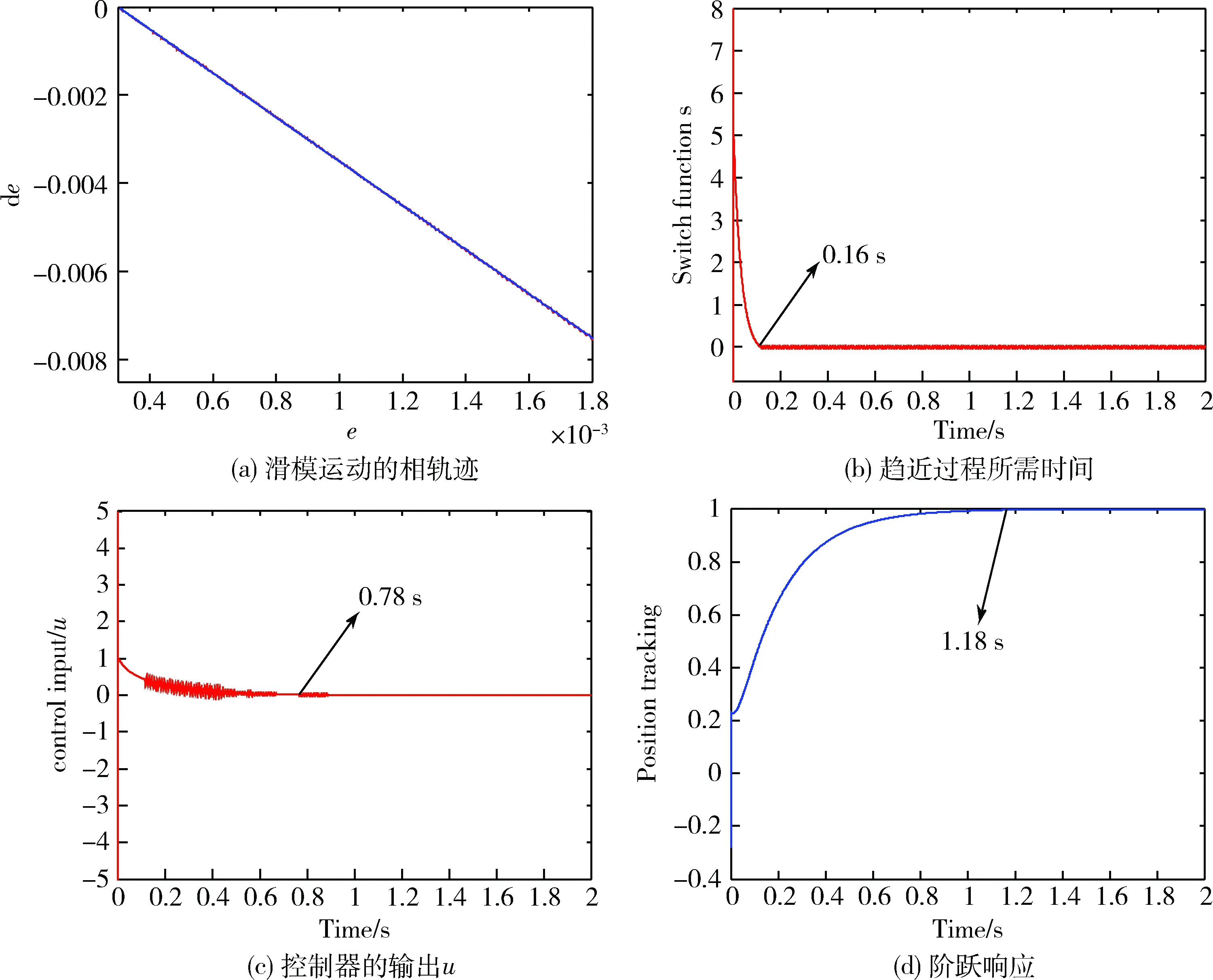
图2 基于NTSM系统仿真曲线

综上，本文通过一个典型二阶系统分别对传统线性滑模面和NTSM滑模面进行了基于MATLAB/Simulink的仿真，通过对比两种不同滑模面的仿真结果，可以得出本文设计的NTSM滑模面相较传统线性滑模面具有更快的趋近速度和响应速度。由于PMSM也为二阶离散系统，可将此NTSM滑模面应用于PMSM控制系统中，提升PMSM的控制精度和响应速度。

2 PMSM非奇异SMC控制策略

2.1 PMSM数学模型的搭建

本文采用id=0的表贴式永磁同步电机转子磁场定向控制，建立d-q坐标系下的数学模型，电压方程为：

(7)

式中：ud、uq分别为d、q轴的电压；id、iq分别为d、q两轴的电流；Ld、Lq分别为d、q轴的电感；R为定子电阻；ω为电角速度。

PMSM的运动方程为：

(8)

式中：Te为PMSM的转矩；TL为负载转矩；J为转动惯量。

永磁同步电机的转矩方程为:

(9)

式中：Te为永磁同步电机的转矩；p为电机极对数；ψ为永磁体和定子的交磁磁链。

针对本文设计的PMSM为目前应用最为广泛的表贴式PMSM，该电机d轴磁感Ld与q轴磁感Lq大小相等，故有:

(10)

2.2 非奇异Terminal滑模面的设计

根据SMC控制策略，令PMSM状态变量为:

(11)

结合式(9)和式(11)，分别对x1和x2微分可得：

(12)

采用本文所设计的NTSM滑模面，可得滑模面s为:

(13)

对s微分可得:

(14)

本文参考文献[20]的最优参数选取，取NTSM设计参数α=3，β=5，λ=1。

为了提高速度趋近运动阶段的动态品质，采用运用较为广泛的等速趋近率，表达式为：

(15)

等速趋近率在实际控制过程中，趋近速度受到符号函数sgn(s)影响较大，可能会激发控制系统中未建模的高频成分，产生较严重的抖振现象[21-22]。为了解决指数趋近率中的存在的问题，本文采用饱和函数sat(s,θ)代替等速趋近率中的符号函数sgn(s),则趋近率为：

(16)

其中sat(s,θ)表达式为:

(17)

结合式(12)、式(14)、式(16)可得控制系统中的电流表达式为:

(18)

3 模糊控制器的设计

由于滑模变结构控制过程中控制系统的控制力是有限的，导致只能施予滑模上运动点有限的加速度，而滑模上的运动点受系统惯性的影响，在控制开关切换前后会出现滞后现象，从而造成抖振[23]。抖振现象在滑模运动中是必定存在的，它会在原本光滑的滑模面上叠加一个锯齿形轨迹，如图3所示，会较大程度上影响到系统的控制精度。针对抖振现象，以降低抖振为目标设计模糊规则，通过设计模糊控制器，实现降低抖振目的。

图3 抖振现象示意图

由上述模糊规则，可定义模糊控制器中的输入模糊集和输出模糊集：

(19)

Δε={NBNMZOPMPB}

(20)

式中，NB为负大，NM为负中，ZO为零，PM为正中，PB为正大。

可得模糊控制器的隶属函数如图4所示。

图4 模糊控制器隶属函数

输入与输出对应的模糊规则为：

(21)

将其带入式(21)中，可得电流方程为:

(22)

其中加入模糊控制器的NTSM控制框如图5所示。

图5 模糊滑模变结构控制框图

4 仿真和实验验证

为了验证本文提出的基于NTSM模糊滑模控制策略的有效性，基于MATLAB/Simulink搭建了电机控制系统仿真模型，并基于芯片TMS320F28335搭建了电机性能测试平台，其中图6为电机控制系统仿真模型控制框图，图7为电机性能测试台架。

图6 电机控制系统仿真模型控制框图

电机控制系统在PID控制策略、普通SMC控制策略、基于NTSM模糊滑模控制策略三种控制策略下的启动响应如图8所示，启动过程中仿真系统收到的转速指令为800 r/min，图9为仿真系统于0.3 s收到15 N·m的突增负载指令时的转速响应，图10为仿真系统于0.5 s时收到-15 N·m的突卸指令时的转速响应。图11(a)、(b)分别为PID控制策略、基于NTSM模糊滑模控制策略仿真系统负载转矩追踪曲线。

图7 电机性能测试台架

图8 起动过程转速仿真曲线

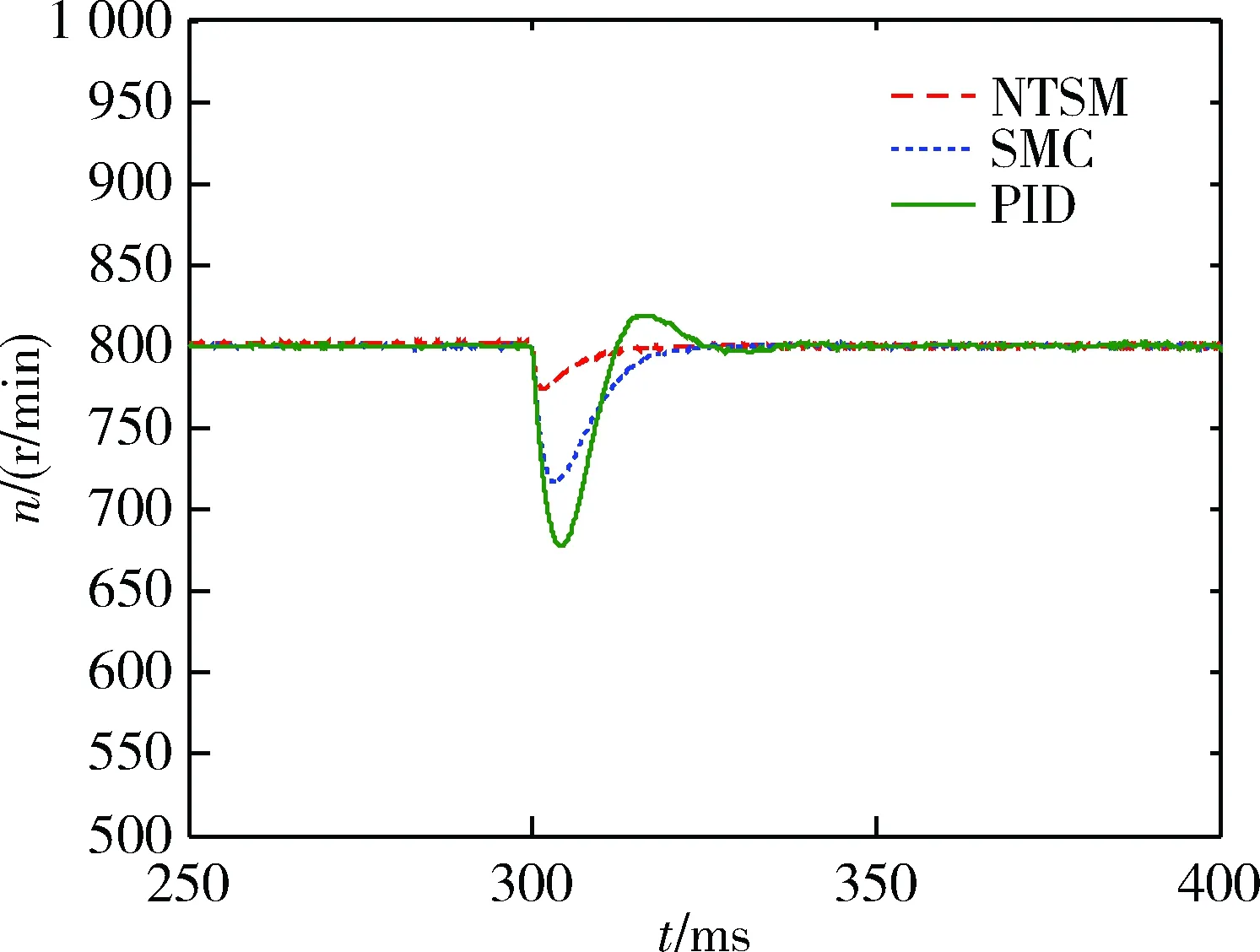
图9 突增负载转速仿真曲线

图10 突增负载转速仿真曲线

图11 负载转矩追踪仿真曲线

分析和对比上述仿真结果可知，当电机控制仿真系统收到800 r/min的启动指令时，如图8所示，PID控制策略启动过程中达到稳态时的响应时间约为46 ms，且存在明显的超调现象，转速最大波动达到300 r/min，启动过程十分不稳定；传统SMC控制策略启动过程中达到稳态时的响应时间约为31 ms，且启动过程中无超调现象，启动性能优于PID控制策略；本文提出的基于NTSM模糊滑模控制策略启动过程中达到稳态时的响应时间约为17 ms，与PID控制策略和传统SMC控制策略相比，启动响应速度分别提升了63%和45%。

当电机控制仿真系统于0.3 s收到15 N·m的突增负载指令时，如图9所示，PID控制策略达到稳态所用时间约为40 ms，最大转速波动约为140 r/min，且在转速调节过程中具有超调现象；传统SMC控制策略达到稳态时所用时间约为28 ms，最大转速波动约为88 r/min，转速调节过程中无超调现象；本文提出的控制策略达到稳态时所用时间约为24 ms，相较PID控制策略和传统SMC控制策略，调节速度分别提升了40%和25%。最大转速波动约为28 r/min，相较PID控制策略和传统SMC控制策略，最大转速波动分别削减了81%和56%。

电机控制仿真系统于0.5 s收到-15 N·m指令时，如图10所示，PID控制策略突卸负载时达到稳定转速的调节时间约为48 ms，最大转速波动大约为135 r/min；传统SMC控制策略达到稳定转速的调节时间约为25 ms，最大转速波动约为91 r/min；本文控制策略达到稳态时的调节时间为22 ms，最大转速波动约为25 r/min。对比图9、图10可得，电机控制仿真系统突卸负载时转速响应曲线与突增负载时转速响应曲线结果相似，进一步验证了本文提出控制策略具有较好的动态性能和抗干扰性。

电机控制系统的负载转矩追踪仿真曲线如图11所示，当系统在0.3 s受到20 N·m的突增负载指令时和-20 N·m突卸负载指令时，PID控制的转矩波动约为5 N·m，转矩达到稳定的调节时间约为35 ms；相较PID控制策略，ISMC控制策略达到转矩稳态的过程中几乎无超调，且转矩能瞬时到达给定转矩指令值，转矩达到稳定时较PID控制策略波动较小，具有较好的稳态性能。

电机测试台架在起动过程时PID控制策略和本文控制策略的试验波形如图12所示,突增负载时的试验波形如图13所示，突卸负载时的试验波形如图14所示，三相电流波形如图15所示。

图12 起动转速响应试验波形

图13 突增负载转速响应试验波形

图14 突卸负载转速响应试验波形

图15 三相电流响应试验波形

由上述仿真试验结果可以得出：

(1)启动过程中，如图8和图12所示，PID控制策略启动速度较慢，且在调节过程中存在超调现象，普通SMC控制无超调现象，启动速度相较PID控制策略有明显提升。本文提出的基于NTSM滑模面的模糊滑模控制策略达到稳态时与前两种控制策略相比，响应速度分别提升了63%和45%，具有较好的启动响应性能。

(2)突增和突卸负载时，如图9、图10、图13、图14所示，PID控制策略达到稳态的调节速度较慢，且调节过程存在较明显的超调现象。传统SMC控制策略在调节过程中无超调现象，但受到SMC控制中抖振现象的影响，转速波动较大。本文控制策略通过设计模糊控制器，使得转速波动较小，这也是本文控制策略中有效抑制抖振现象的体现，且通过NTSM代替传统滑模面，使得调节速度较SMC控制策略有明显提升，展现出了较好的动态性能和鲁棒性。

(3)控制过程中的三相电流响应，如图15(a)(b)所示。本文控制策略的三相电流响应较PID控制更加平稳，达到稳态时电流波动较小，说明本文设计的基于NTSM模糊滑模控制器具有较好的抗干扰性和稳态性能。

综上分析，本文设计的NTSM模糊滑模控制策略，通过采用NTSM代替传统SMC控制策略中的线性滑模面，有效地提升了电机控制系统的响应速度和调节速度。通过以降低抖振为目的设定模糊规则，通过模糊控制器不断调整控制增益使得电机控制系统受到外界负载干扰时转速波动明显减少，体现出了较好的动态性能和稳态性能。

5 结论

本文针对PMSM现有控制策略收敛时间长的问题，在传统SMC控制策略的基础上，提出采用NTSM代替线性滑模面进行控制，以加快系统收敛速度；针对SMC控制上普遍存在的抖振现象，设计模糊控制器进行有效削减。通过MATLAB/Simulink仿真和电机性能测试台架试验，结果表明：本文提出的NTSM模糊控制策略能有效加快系统收敛速度，提高响应性能；能有效抑制抖振现象，提高动态性能和稳态性能。本文提出的策略为实现PMSM高精度、高效率的控制提供一种有效的新方法。