无线Ad Hoc网络MAC层中针对FD中继的高效空间复用机制

宋 宇，齐望东，赵卫伟

(1. 陆军工程大学 指挥控制工程学院，江苏 南京 210007; 2. 国防科技大学 试验训练基地，陕西 西安 710106)

0 引言

在无线自组织网络(Wireless Ad Hoc Networks,下简称网络)中，当一个节点所发送数据帧的目的节点超出了其传输范围(Transmission Ranges，TR)时，它需要经过中继节点转发。近年来，随着模拟域、数字域自干扰(Self-Interference，SI)消除技术的进步，节点可以实现同时同频全双工(Full-Duplex，FD)通信[1]。当中继节点以该模式工作时，其两侧的链路可以同时工作。但是，中继节点以FD模式工作也带来了新的干扰样式。为此，有必要在媒体访问控制层(Media Access Control，MAC)设计新的机制。

基于载波侦听多路访问(Carrier Sensing Multiple Access，CSMA)机制[2]广泛应用于半双工(Half-Duplex，HD)网络的MAC层[3-4]，在发送端发送信号期间，位于其载波侦听范围(Carrier Sensing Range，CSR)内的节点都会侦听到信道忙，不会发送信号[5]。为了避免隐蔽终端问题，典型的方法是要求位于接收端干扰范围(Interference Range，IR)内的节点在它接收帧期间始终能侦听到发送端的发送信号。该方法同样适用于FD网络。但是需要解决以下几个新问题。

发送端的CSR大小由其发送功率决定。假设链路速率固定，网络容量大小取决于每条链路的有效吞吐率和网络中可同时工作的链路数量。以节点A、B、C建立的两跳路径为例。为了增加网络的空间复用，B不管是单纯地向A发送反向信号(B未产生有效吞吐)，还是作为A到C的帧传输中继(后续为表达方便，将这两种模式分别简称为FD模式1和FD模式2)，FD MAC机制都需要尽可能地减小各发送端的发送功率以减小它们的CSR。当B以FD模式1工作时，A只能将Data帧发送至B，B需要再次发起到C的Data帧传输。当B以FD模式2工作时，A可以直接将Data帧发送至C。如果不考虑控制帧开销，后者吞吐率是前者的两倍。但是，当B以FD模式1工作时隐蔽终端只在其周围存在。当B以FD模式2工作时隐蔽终端同时在B和C周围存在，为了避免传输干扰，可能需要两个发送端使用较大发送功率。

为此，FD MAC机制需要在吞吐增益和占用空间大小问题上权衡B的模式选择。具体地，分别建模和求解在FD模式1和2下两个发送端发送功率的优化模型。随后，通过对比在两种不同模式下两跳路径的吞吐率和占用空间大小以决定它们采用的通信模式。

1 系统模型

以节点A、B、C建立的两跳路径为例。将各发送端最大发送功率标记为Ptmax。将A的发送功率标记为PtA。DataA→B和TDataA→B分别标记由A发送至B的数据帧以及其传输时间。B接收来自A的信号强度以及信噪比分别以PrA→B和SINRrA→B标记。类似地，有PtB，DataB→C，TDataB→C，PrA→C，PrB→C以及SINRrB→C等标记。此外，B还可以向A发送反向信号，以PrB→A标记A接收来自B的信号强度。注意该信号对于当前路径没有产生有效吞吐。PrA→B由式(1)给定：

(1)

其中，DAB标记A和B之间的距离，c为常数。类似地，可以获得PrA→C和PrB→C的表达式。SINRrA→B由式(2)给定：

(2)

其中，PnB标记B所受到的总干扰功率，有：

(3)

Psthold代表节点侦听到信号的最小功率界。SINRthold代表最小节点成功接收信号的最小SINR界。将CSRA(PtA)标记为A的CSR。位于CSRA(PtA)内节点的接收信号需要满足Psthold约束。由CSRA(PtA)所围成的区域被认为是A发送信号占用的空间大小，将其大小标记为S(CSRA)。类似地，有CSRB(PtB)以及S(CSRB)。将CSRAB(PtA,PtB)标记为A和B同时发送信号所形成的CSR，将其大小标记为S(CSRAB)。IRB(FD)代表B以FD模式工作时的IR。由式(1)～(3)可得：

(4)

其中，c′由B以及与它最近且没有干扰到B接收的节点天线的高度和增益决定。尽管C是以HD模式接收帧，但是，它会受到来自A的发送信号干扰。以IRC(HD)标记C的IR，简写为IRC(HD)，其表达式如下：

(5)

为简化讨论，假设各发送端天线高度和增益相同，c′和c均为1。同时令Pn=0。

2 针对FD中继的MAC层高效空间复用机制

首先，分别针对B的两种FD模式，计算各发送端的最优发送功率。随后，分别求解在FD模式1和2下两跳路径所占用的空间大小。

2.1 针对B发送补充信号时的功率控制方法

在接收DataA→B帧期间，B可以发送补充信号，以避免其接收数据帧时的隐蔽终端问题[6]。此时，A和B之间的通信链路占用空间的大小由二者的发送信号共同决定。必须联合求解PtA和PtB。

在A、B同时发送信号期间，为确保B对DataA→B帧的接收不被干扰，不允许位于IRB(FD)内的节点发送信号。具体地，要求CSRAB(PtA,PtB)覆盖IRB(FD)。将CSRAB(PtA,PtB)和IRB(FD)在极坐标中建模，如图1所示。将A的位置作为原点(0,0)，向量AB的方向作为θ=0方向，Q是该方向上的一个位置。将B与Q的距离标记为DBQ。令DBQ=IRB(FD)。在某个θ方向上，假设M是可以侦听到A和B发送信号的最远位置。令：

DAM=rmax(θ)

(6)

图1 极坐标系中CSRAB(PtA,PtB)和IRB(FD)的示意图

由DAM和DAB，根据余弦定理，可得DBM。进一步地，由M位置的定义，根据Psthold定义，有式(7)成立：

(7)

若给定(PtA,PtB)值，结合DBM，可以通过启发式方法求解rmax(θ)。该rmax(θ)即为在某个θ方向上CSRAB(PtA,PtB)的值。

注意到求解PtA和PtB的目标是使得S(CSRAB)尽量小并且要求IRB(FD)必须被CSRAB(PtA,PtB)覆盖。首先，讨论PtA和PtB取值的可行域。由于IRB(FD)边界上的各个位置与B的距离相同而与A的距离不同，所以在这些位置上由B的发送信号产生的接收信号强度相同而由A的发送信号产生的接收信号强度不同。注意到IRB(FD)边界上的Q位置距离A最远，所以A的发送信号在该位置产生的接收信号强度最小。因此，给定(PtA,PtB)，如果有下面的条件成立：

rmax(θ)|θ=0≥DAB+IRB(FD)

(8)

即节点在Q位置上可以侦听到来自A和B的发送信号，则整个IRB(FD)可以被CSRAB(PtA,PtB)覆盖。此时，M位置也就一定位于IRB(FD)之外。进一步地，式(9)给出了PtA和PtB需要满足的约束：

(9)

满足式(9)的PtA和PtB取值即为二者的可行解。下面根据(PtA,PtB)解的可行域中二者具体取值利用积分的思想近似求解S(CSRAB)。在图1中，以Δθ标记θ的增量。假设N是在θ+Δθ方向上可以侦听到A和B发送信号的最远位置。令：

DAN=rmax(θ+Δθ)

(10)

给定PtA和PtB取值，同样采用启发式方法求解rmax(θ+Δθ)值。从M和N位置向AB垂线，令交点分别为M′和N′。DMM′、DNN′以及DM′N′的值可以由基本的三角函数关系获得。根据它们的值，可以得到由M、M′、N以及N′所围成的梯形区域面积，标记为SMM′N′N。

为了求解S(CSRAB)，可以将[0,π]划分为若干Δθ。随后，采用上述方法求解每个θ变化区间由A和B发送信号强度所围成的梯形面积。将它们累加起来乘以2即为S(CSRAB)的近似值。在PtA和PtB取值的可行域中，使得S(CSRAB)取得最小值的PtA和PtB组合即为该模式下的最优解。

2.2 针对B作为FD中继时的功率控制方法

在接收DataA→B帧期间，B可以以FD模式将该帧直接中继给C。在信号层面上，该模式下也是A和B同时发送信号。此时PtA和PtB除了需要确保B对DataA→B帧的接收不被干扰外，还需要避免当C接收信号时其周围可能存在的隐蔽终端问题。也就是说，在A和B同时发送帧期间，要求CSRAB(PtA,PtB)同时覆盖IRB(FD)和IRC(HD)。前一个覆盖条件与上一节讨论一致，下面主要讨论后一个覆盖条件。

当B作为A向C发送数据帧的中继节点时，尽管C是以HD模式接收来自B的数据帧，但是由式(5)，IRC(HD)与PtA、PtB、DBC以及DAC均相关。图2采用的极坐标系与图1一致。分别延着向量AC和BC方向作延长线，将二者与IRC(HD)边界的交点标记为P和Q。此外，IRC(HD)还分别与AC和BC(或者是二者反方向的延长线)相交。将这两个交点标记为A′和B′。图2所示为前一种的情况。下面讨论要求IRC(HD)必须被CSRAB(PtA,PtB)覆盖条件对PtA和PtB可行域的约束。

图2 极坐标系中CSRAB(PtA,PtB)和IRC(HD)的示意图

在PB′弧(该弧在IRC(HD)边界上)的各个位置上，P位置对于A和B来说都是最远的位置。所以，节点在该位置接收到的来自二者的发送信号强度最小。同理，在QA′弧的各个位置上，节点在Q位置接收到的来自A和B的发送信号强度最小。所以，在数据帧发送期间，为了让PB′弧和QA′弧上面的节点不发送信号，只需让处于P和Q位置的节点侦听到A和B的发送信号强度即可。当节点沿着PQ弧(或QP弧)移动时，节点与其中一个发送端的距离增大，而与另一个发送端的距离减小。此时，如果节点在端点P和Q位置上可以侦听到两个发送端的发送信号强度，则近似认为节点在位于PQ弧的各个位置也能侦听到。所以，将避免C接收帧被干扰的条件建模如下：

(11)

(12)

由余弦定理，可以获得DAQ和DBP的值。将B作为FD中继节点中继A到B数据帧传输，要求PtA和PtB必须满足这两个公式和上述公式(9)。在(PtA,PtB)所有可行解中使得S(CSRAB)取得最小值的解即为该问题的解。与上述方法一致，不再赘述。

以单位面积吞吐率测度判定B的FD模式在仿真分析中讨论。

3 仿真分析

分别取SIB=1×10-9以及5×10-9。给出B分别以FD模式1和2工作时S(CSRAB)的数值仿真及分析。在此基础上，讨论B应采用的FD模式。

3.1 B节点以FD模式1工作时S(CSRAB)的数值仿真及分析

该模式下B接收DataA→B帧期间仅发送反向信号。随着DAB和SIB的变化，S(CSRAB)如图3所示。

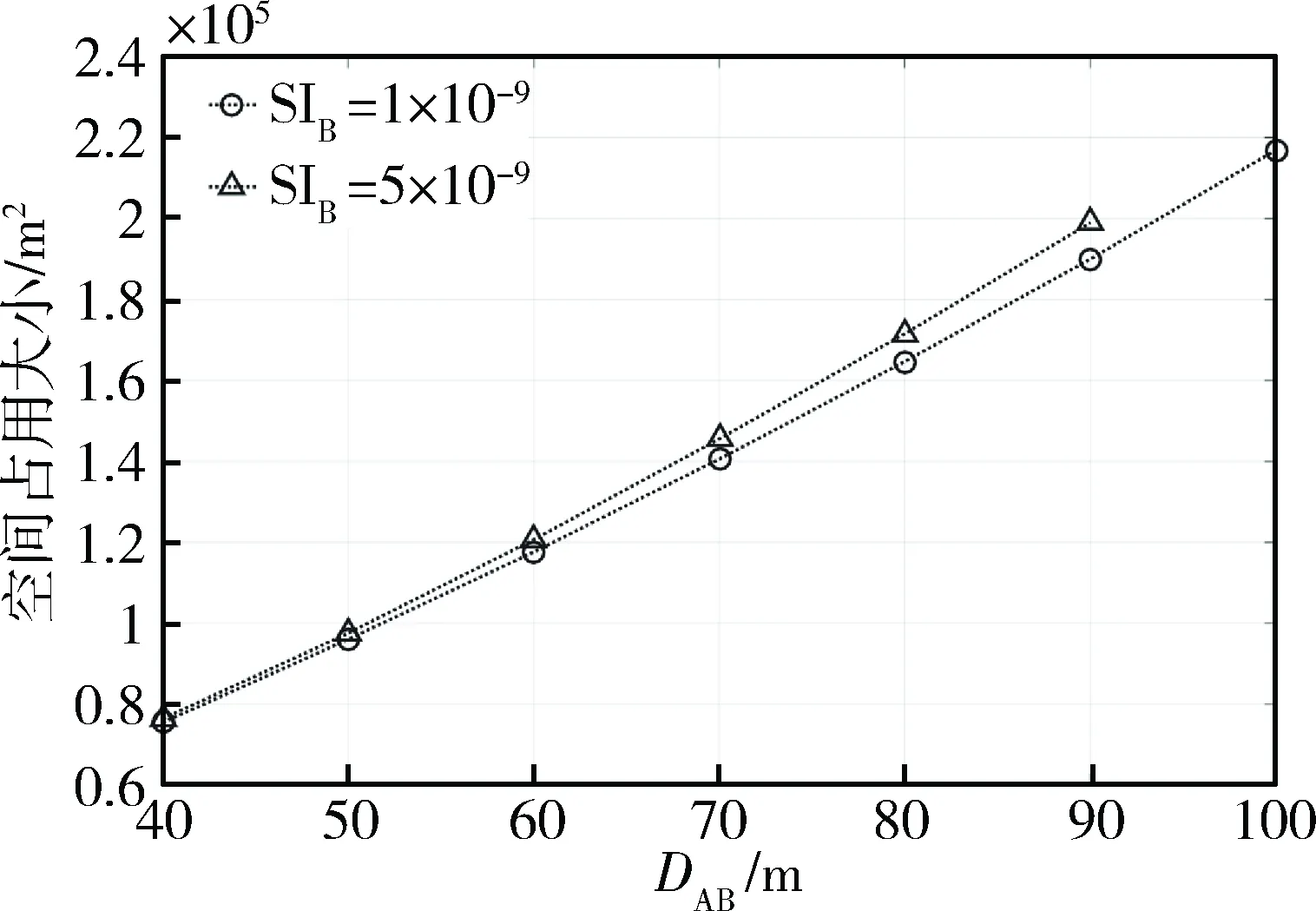
图3 根据DAB和SIB取值的不同S(CSRAB)的变化示意图

假设PtA不变，随着DAB增大，PrA→B会减弱。同时，由于SIB≠0，当B发送补充信号时它会有自干扰。这两个因素均会降低SINRA→B。所以，在SIB两种取值下，随着DAB增大，PtA均会增大。保持DAB不变，当SIB由1×10-9增大到5×10-9时，相同的PtB会产生更大的自干扰。为确保DataA→B帧的正确接收，PtA和PtB分别需要增大和减小。对应地，S(CSRAB)有略微增大，如图3所示。由于在该模式下其他节点并不需要接收B发送的信号，对PtB的约束只是让S(CSRAB)尽量小，所以，当PtA随着DAB增大时，有可能与该PtA只需要搭配一个较小的PtB值即可满足约束(9)。仿真中发现，随着DAB变化，PtB的变化并无明确的单调性。需要说明的是，当DAB=100 m时，PtA和PtB在SIB=1×10-9情况下有解(尽管此时PtB值很小)，而在SIB=5×10-9情况下无解。这是因为在该DAB和SIB取值下，即使是很小的PtB也需要足够大的PtA以确保DataA→B帧的正确接收，但是所要求的PtA值大于Ptmax。

3.2 B节点以FD模式2工作时S(CSRAB)的数值仿真及分析

该模式下B接收DataA→B帧的同时需要发送DataB→C帧。为简化讨论，仅选取DAB=40 m和60 m两种情况。假设图2中φ=5π/6，随着DAB、DBC、SIB的变化，S(CSRAB)分别如图4和5所示(针对SIB取值的两种情况分别展示)。

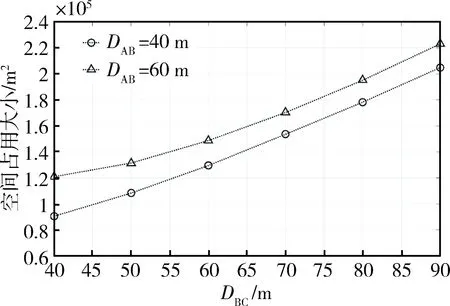
图4 当SIB=1×10-9时根据DAB和DBC取值的不同S(CSRAB)的变化

图5 当SIB=5×10-9时根据DAB和DBC取值的不同S(CSRAB)的变化

不论SIB=1×10-9还是5×10-9，若保持DAB和PtB不变，随着DBC增大，PrB→C会减弱。为确保DataB→C帧的正确接收，PtB会增大。类似地，保持DBC不变，随着DAB增大，为确保DataA→B帧的正确接收，PtA会增大。相应地，随着DAB和DBC增大，S(CSRAB)会增大，如图4和5所示。仿真中发现，当DBC取较大值时(图4中DBC取80 m或90 m，图5中DBC取60 m或70 m), 随着DAB增大，除了PtA增大外，PtB也会增大。这是因为PtA增大会扩大IRC(HD)，尽管PtA增大使得CSRAB(PtA,PtB)扩大，但是由于A距离C较远，该扩大的CSRAB(PtA,PtB)不足以覆盖扩大后的IRC(HD)，所以需要适当增大PtB。而当SIB=5×10-9时，PtB增大会产生较大的自干扰，为确保DataA→B帧的正确接收，PtA需要进一步增大。所以，当DAB增大到一定程度时，所要求的PtB大于Ptmax。比如，当DAB=60 m，DBC=60 m或90 m时，(PtA,PtB)无解。

3.3 节点之间通信模式的选择

当SIB=1×10-9时，对应DAB=40 m和60 m，当B以FD模式1工作时，S(CSRAB)分别为7.54×104m2和11.76×104m2。当B以FD模式2工作时，对应DAB=40 m，S(CSRAB)最小为9.05×104m2(当DBC=40 m时)，最大为20.48×104m2(当DBC=90 m时)。当S(CSRAB)大于两倍的7.54×104m2时(仿真中DBC>70 m)， B不适宜以FD模式2工作。否则，可以以该模式工作以增加单位面积的吞吐率。同样，对应DAB=60 m，S(CSRAB)最小为12.09×104m2(当DBC=40 m时)，最大为22.3×104m2(当DBC=90 m时)。与前面不同的是，该范围内所有S(CSRAB)均无法大于11.76×104m2的两倍。此时，B不宜以FD模式2工作。当SIB=5×10-9时，有类似讨论，不再赘述。

4 结束语

针对无线网络中的两跳路径，可以采用FD节点作为中继节点。针对该节点以FD工作的两种模式，以最小化两个发送端的发送信号占用的空间大小为目标，分别求解了它们的最小发送功率。并提出了单位面积吞吐率测度以让FD中继节点选择所采用的FD模式。给出的数值仿真验证了该机制的有效性。下一步，需要设计相关的控制帧以及协议交互过程，以将该机制融入具体的FD MAC协议。