典型安装架在随机振动下的优化设计*

陈以金，焦春旺，古智祥，张 杰

(中国电子科技集团公司第二十九研究所， 四川 成都 610036)

引 言

近年来，机载电子设备承受的环境条件越来越恶劣，整机单位对电子设备的要求也越来越苛刻。依据经验设计的电子设备产品在一定程度上能够满足要求，但是在恶劣振动环境中如何保证复杂电子设备结构具有较高刚、强度和低质量则面临巨大的挑战，结构优化设计可以解决此类问题[1-2]。随着计算机技术的发展，结构优化设计已经被广泛地应用于航空、航天和汽车等领域[3-6]。

对电子设备而言，设计之初引入结构优化设计方法可以缩短产品的研发周期，节约制造成本和提高产品的设计质量。文献[7]对框架结构(转笼)的模态进行了优化设计，并通过试验对优化结果进行了验证。文献[8]对舰载机柜的模态进行了优化设计，进而根据试验数据进行了再设计，使舰载机柜具有较强的抗冲击性能。文献[9]对某型雷达天线壳体在静载荷作用下进行了优化设计，在应力和变形满足要求的前提下减重19%。文献[10]对某机载碳纤维显控台进行了模态分析，依据分析结果对显控台结构进行了优化，成功降低了正弦激励条件下的位移响应幅值。

目前的优化设计主要致力于解决静力学、模态和频率响应条件下的优化问题，对于直接解决其他类型动力学问题的案例报道较少。当前市面上的绝大多数商业软件都不支持在随机振动条件下直接对结构进行等效应力(均方根)的优化设计。文中项目对某通用电子设备的典型安装架进行规划使用时，发现存在较大的风险。由于安装架及其负载在新研项目中主要承受随机振动载荷，因此本文将重点研究安装架在随机振动条件下的优化设计，探索利用优化软件解决部分产品在动力学环境下的结构优化设计的可行性问题。

1 原安装架力学仿真分析

1.1 研究对象

文中以机载平台某通用电子设备的典型安装架为研究对象，满足单位常用ATR分机(前紧定)及通过法兰进行安装的分机的安装要求。此安装架实物前期已经在某型号项目中配合多个分机交付使用，现场反馈实物运行良好。值得注意的是，安装架实物在前期使用中被置于带有减振器的机柜中，环境条件较好，因此不易出现问题。考虑到某新研项目可能会在无减振措施的环境中使用此安装架，且主要环境条件为随机振动，直接使用此安装架将存在较大的风险。因此本文将对原始安装架(包含分机)进行动力学仿真分析，考察原始安装架是否满足新研项目环境要求。新研项目规划的分机通过法兰进行连接，因此本文对原安装架用于ATR分机连接的安装孔位进行了简化处理，仅保留了分机法兰安装接口和对外安装接口。简化后的原始安装架和分机组装模型如图1(a)所示，包含分机、安装架和左右导向条，安装架的背面模型如图1(b)所示。

图1 原始安装架和分机的简化三维模型

1.2 仿真条件和基本设置

依据总体前期规划，分机对安装架的安装接口保持不变，最大质量不超过20 kg。安装架对分机接口和对外接口皆采用不锈钢螺钉进行刚性连接。考虑到实际分机重心可能有所偏移，仿真分析时假设分机质量为25 kg(通过施加集中质量予以实现)，但质心位于几何中心处。仿真分析采用了Altair公司的商业分析软件HyperWorks V14.0中的HyperMesh和OptiStruct模块。安装架材料为硬铝合金(2A12)，导向条和分机材料为防锈铝合金(5A06)，材料参数如表1所示，随机振动条件如表2所示。

表1 结构材料力学性能参数

表2 随机振动试验条件

注：总均方根值grms=13.7 m/s2；X、Y、Z每方向振动时间：60 min。

1.3 仿真结果

1.3.1 模态结果

模态分析主要用于获取结构的模态频率和对应的基本变形模式，可以用于评估系统的振动特性以及组件和其支撑结构的动态相互关系，其计算结果是随机振动分析的基础。分机和安装架前6阶的模态结果如表3所示。

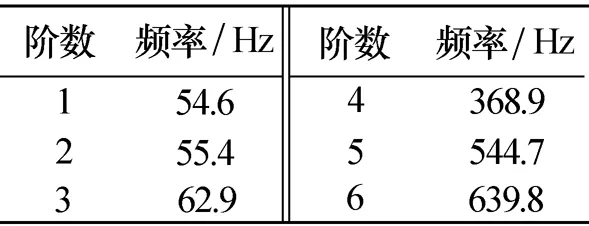
表3 原设计安装架及分机模态结果

1.3.2 应力和变形结果

本文重点关注安装架的应力和变形情况，因此下文仅给出安装架的应力和变形结果。考虑到篇幅原因，仅给出X方向激励下安装架的应力和变形云图(图2)，其余应力和变形结果统计如表4所示。

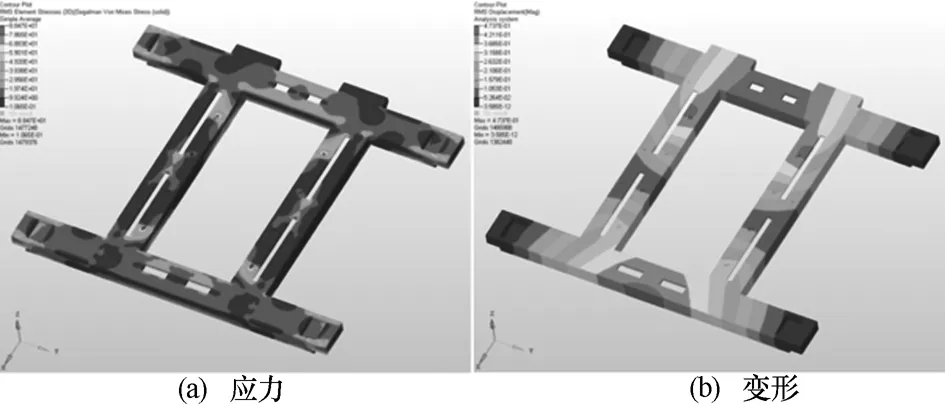
图2 X方向激励下的应力及变形云图

表4 原设计安装架随机振动分析结果

考虑到安装架与分机在实际连接时采用了螺钉和钢丝螺套的连接方式，而仿真时未考虑钢丝螺套，因此本文在给出仿真结果时已经去除钢丝螺套在安装架中所占空间的单元应力(即未考虑连接处局部应力的影响)。根据仿真结果可以看出，X向施加激励时等效应力最大，如果按照3σ原则进行强度判定，此方向激励时的3σ最大等效应力高达265.5 MPa。考虑到安装架材料屈服强度为275 MPa，安全裕度仅为275/265.5=1.04，不满足金属材料1.3倍安全裕度要求，因此本文将针对安装架模型进行优化设计。

2 安装架拓扑优化

2.1 优化设计思路

考虑到本文的目的是探索利用优化软件进行安装架在随机振动条件下的优化设计的可行性，因此暂不考虑多种参数变化对优化结果的影响，如分机的质量、质心、安装位置等，仅考虑一种在确定质量(最大25 kg)、质心(几何中心)、安装孔位条件下，法兰连接安装架的优化设计情况。以此为安装架优化设计经验进行推广，将优化方法延伸至其他不同应用场景之中。

本文最初优化设计思路是基于原安装架进行优化，后面在探索过程中发现原安装架由于其结构形式已经固化，再进行优化设计效果不甚明显。因此，本文重新调整策略，在考虑对内对外接口不变的前提下，基于减重前的安装架基础结构进行优化设计，在保证优化后质量与原设计模型相同的条件下，降低其最大等效应力和变形。考虑到本文研究的安装架模型承受的外载为基础激励，因此采用静力等效思路将随机振动载荷转化为静力载荷，具体操作方法如下：首先根据随机振动条件计算加速度均方根值，然后基于此进行加载，接着在此基础上调整静载量值，使结构在随机振动和静载下的最大变形值相同，后文中的拓扑优化将基于此静载进行仿真。值得注意的是，本文之所以选择变形值相同而不选择应力相同进行等效，主要是考虑到网格质量、加载方式等对应力量值的影响较大。此外，根据仿真结果可以看出，最大等效应力仅存在于局部位置，而最大变形值却出现在结构的大部分区域，因此选择变形值等效与结构实际受力情况更接近。

2.2 优化求解设置

概念设计是为后续设计提供一个定性的参考，且本文的最终目的是对安装架在随机振动条件下进行优化设计，因此这里不适合采用应力或者位移作为拓扑优化的约束条件。体积分数是全局响应，其取值范围为0～1，表示拓扑优化相对于初始设计空间的分数。加权柔度是在典型拓扑优化问题中使用的一种考虑多个子工况(载荷步、载荷工况)的方法，是每一子工况的柔度的加权和，也是定义在整个结构上的全局响应。因此，本文选择体积分数响应和加权柔度响应，设置体积分数为约束条件，最大值为0.4，优化目标的同时考虑3个方向静载下加权柔度最小(即刚度最大)。安装架基础结构有限元模型如图3所示，安装架中间区域为设计区域，中间螺纹孔和4个边缘分别为分机接口和对外接口，其尺寸有特定要求，在拓扑优化中不能改变。

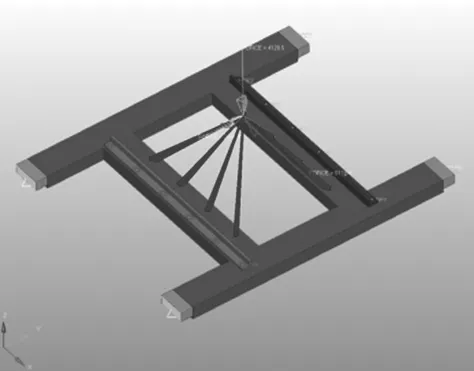
图3 安装架基础结构有限元模型

2.3 优化仿真结果

在综合考虑最小尺寸约束、棋盘格控制、离散度和工艺加工方向以后，最终得到的拓扑优化结果如图4所示。Y向横梁中间部分被优化掉，X向横梁分机中间安装孔周围区域被优化掉，仅留下部分加强筋。此优化结果为后续概念设计提供思路。

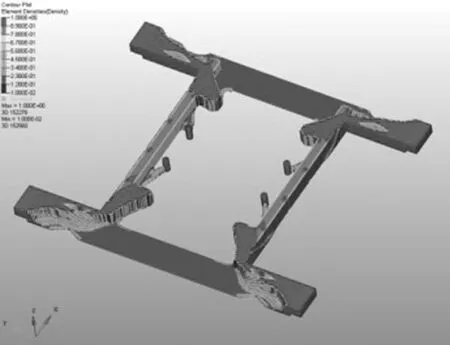
图4 拓扑优化结果示意图

3 优化设计模型和力学仿真分析

3.1 安装架优化模型

基于随机振动条件优化后得到的初始三维模型如图5(a)所示，通过观察可以发现，由于施加到安装架上的载荷和边界条件沿XZ平面呈现出明显的对称性，因此基于优化仿真得到的安装架模型也沿XZ平面呈现出明显的对称性。优化后的安装架中间部分沿Y方向刚度相对较弱，因为其中间部分没有载荷安装点，且不处于主要传力路径上。实际实验过程中安装架对外接口并非与仿真完全吻合，可能会出现4个约束部位加载不完全一致的情况，以及分机质心偏离几何中心的情况。根据设计经验，本文在初始优化得到的三维模型的基础上沿Y方向增加了2条加强筋，用以提高安装架本身的刚度，最终得到的三维模型如图5(b)所示。

图5 拓扑优化设计的初始和最终安装架模型

3.2 安装架仿真分析

3.2.1 模态分析

在保证优化后质量不高于初始设计模型的基础上(优化前1 000 g，优化后995 g)，优化前和优化后安装架及分机整体模型的模态比较情况如表5所示，本文主要截取了前6阶模态进行比较。观察发现，除了第5阶频率略微有所降低(仅1.6%)，其余5阶频率全部提升明显，最大提升量达60.8%，最小提升量也高于34.3%。综合考虑，由于低阶模态在本文研究结构中所起的作用更大，因此优化后安装架和分机整体刚度提升效果显著。

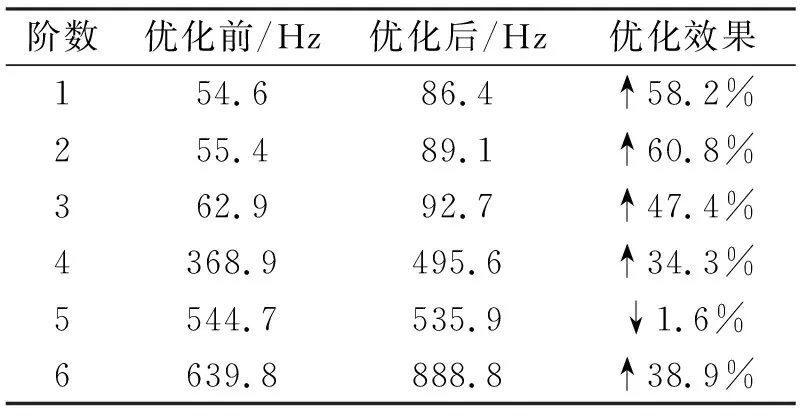
表5 优化前后安装架及分机模态比较

3.2.2 应力和变形结果分析

如上文所述，本文重点关注安装架的应力和变形情况，因此图6给出优化后安装架在X方向激励下的应力和变形结果，其他方向结果将在表6中进行统计。

图6 X方向激励下的应力及变形云图

基于仿真分析，表7给出了优化前后安装架在随机振动载荷下的应力和变形结果。通过观察可以发现，3个方向的最大等效应力和变形都有所改善。应力最佳优化效果可以达到53.6%，变形最佳优化效果可以达到56.5%。优化后安装架的应力分布更加均匀，表明材料利用率更高，构型更趋于合理。优化后最大等效应力出现在Z向激励时，3σ最大等效应力为156 MPa，考虑到安装架材料屈服强度为275 MPa，安全裕度为275/156=1.76。

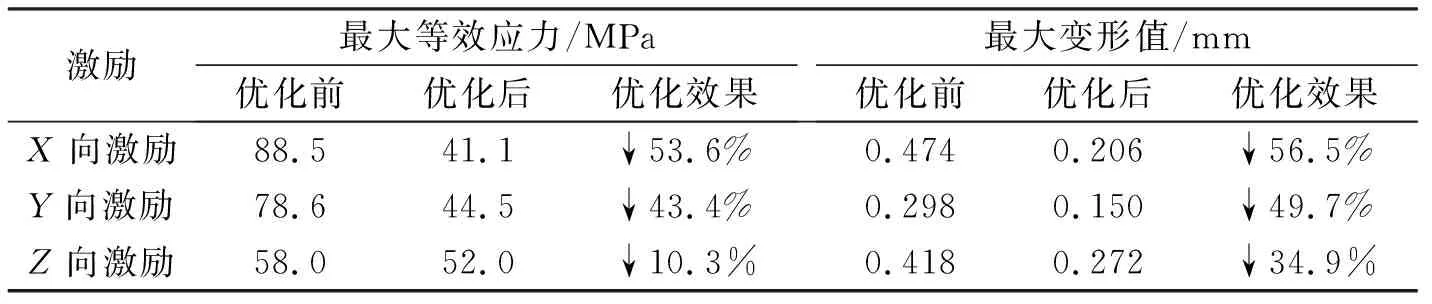
表6 优化前后安装架模型应力变形结果比较

4 试验验证

为了进一步验证基于优化仿真的安装架是否满足环境试验条件，本文制作了安装架实物模型和分机质量模拟件，按照表2所述的随机振动条件进行3个方向的振动试验(图7)，每个方向保持60 min。试验完毕检查安装架，无肉眼可见的损伤，且螺钉无明显松动现象，表明通过优化仿真得到的安装架能够满足常规机载设备环境试验要求，静力等效优化思路切实可行，满足工程项目要求。

图7 优化后安装架及分机随机振动试验

5 结束语

针对安装架在随机振动条件下的优化设计，本文采用静力等效思路将随机振动载荷转化为静载荷，对安装架在静力载荷下进行拓扑优化；接着基于拓扑优化结果进行模型设计和动力学仿真分析。分析结果表明，在保证优化后质量不高于原设计模型的条件下，优化后的安装架及分机整体1阶模态提高58.2%，安装架应力减小量值高达53.6%，变形量减小量值高达56.5%，且应力分布更加均匀，表明材料利用率更高，构型更趋于合理。在此基础上，本文还采用随机振动试验对优化后的安装架进行了验证。本文的研究思路和方法为电子设备安装架在动力学载荷下的优化设计提供了工程参考。