一种低成本测量材料杨氏模量的方法*

颜刚毅， 房 凯

(南京电子技术研究所, 江苏 南京 210039)

引 言

杨氏模量是一项极为重要的材料参数，在几何尺寸确定的情况下，材料的杨氏模量直接影响结构的刚度、固有频率等重要结构力学参数。

准确的杨氏模量有利于设计师在对结构进行有限元仿真时得出准确的共振频率、刚度等，有利于进行结构优化设计[1-2]。

杨氏模量的测量已有非常成熟的方法，比如拉伸法，弯曲法，共振法等。拉伸法需要将材料制成细丝状，利用光杠杆以观察测量微小的材料伸长量。而共振法通过测量某个结构的共振频率，利用振动力学公式反推出杨氏模量。这些方法一般都要用到较为复杂的设备及贵重的传感器[3-6]。

本文提出了一种低成本测量材料杨氏模量的方法，将待测材料制成悬臂梁结构，在悬臂梁上贴有压电片，让悬臂梁自由振动，通过压电材料的压电效应将机械振动转换为电信号，直接输出振动波形，通过测量悬臂梁自由振动频率反推出材料杨氏模量。这种方法优点在于试件制作简单，无需贵重的传感器就能实现材料杨氏模量的测量。这种低成本的测量方法在工程上有一定的实用价值。

1 原理

1.1 悬臂梁自由振动方程

根据振动力学计算，一端固定，一端自由的等截面梁的1阶固有频率为：

(1)

式中：E为杨氏模量；I为截面对中性轴的惯性矩；ρ为密度；A为梁截面积；l为梁的长度。

当梁截面为矩形，设宽度为b，厚度为h，则有：

A=bh

(2)

(3)

代入式(1)，可得：

(4)

将杨氏模量E作为待求解量，频率f作为已知量，可得：

(5)

悬臂梁的几何参数可以通过游标卡尺或螺旋测微器测量得到，密度也较容易通过体积质量测量得出，关键在于测量自由振动频率。

1.2 压电传感器

用激光位移传感器、电涡流传感器等都可以测量悬臂梁的自由振动频率，但是这些传感器成本较高，一般单位没有条件采购。本文用压电片作为传感器使用，压电片很容易购买，且成本非常低。

压电材料既能传感又能致动，在智能结构中有相当多的应用[7]。描述压电材料的状态变量有应力T、应变S、电位移D及电场E，四者关系可以用压电方程描述。压电方程根据自变量的不同，共有4 种，这4 种压电方程本质上是等价的。以应变S和电位移D为自变量时，称为h型压电方程：

T=cDS-htD
E=-hS+βSD

(6)

式中：h为压电应变常数；cD为电位移强度D恒定时的弹性模量；βS为应变S恒定时的介电诱导率；下标t表示转置。

当外界测量电阻极大，压电片相当于处于开路状态时，电位移D可认为保持不变，假设初始电荷为0 C，则D=0，这样E=-hS，产生的电场大小仅与应变有关，且成线性比例关系。简单来说，悬臂梁的应变带动压电片产生应变，压电片因压电效应输出电压。压电片的输出电压波形的周期就是悬臂梁振动的周期。

给悬臂梁一初始位移并松开，悬臂梁将处于自由振动状态。此时的频率即为1阶共振频率，将此频率代入式(5)即可得到材料杨氏模量。

2 实验设计与分析

2.1 压电片对悬臂梁固有频率的影响

在悬臂梁上贴压电片，理论上会提升悬臂梁的固有频率。显然，在尺寸一定的情况下，压电片越“软”，对悬臂梁影响越小，压电片越“刚”，影响越大。压电片本身的刚度不仅仅与所用的压电材料有关，也与压电片所处的电连接状态有关，因为压电材料的杨氏模量在开路状态和短路状态略有不同。开路状态时，受外力影响，压电片因压电效应产生的电荷没有回路，整体偏刚性，杨氏模量偏大。而短路状态时，压电片因压电效应产生的电荷可以自由移动，整体偏软，杨氏模量偏小。给压电片接入一定的电阻时，压电片便介于完全开路与完全短路两个状态之间，杨氏模量也处于开路杨氏模量与短路杨氏模量之间。测量压电片输出电压时，外部测量系统与压电片相连，相当于给压电片接入一定的负载，由于测量系统一般要求拥有较大的输入阻抗，所以分析压电片力学性学性能时，可按电学开路状态处理。

压电片的尺寸大小不同对悬臂梁固有频率的影响亦有不同。具体的影响程度需要通过仿真进行定量分析。以尺寸为49 mm × 4.4 mm × 0.39 mm的悬臂梁和尺寸为4 mm × 4 mm × 0.2 mm的压电片为例，压电片左端与梁的固定端距离d定为4 mm，以此为基准条件，仿真各参数变化对固有频率的影响。为了仿真出定量的结果，需暂定待测金属的杨氏模量为141 GPa，泊松比0.33，密度为7 840 kg/m3。

图1 仿真模型

将压电片左端距离梁固定端距离d作为变量，仿真出不同d时悬臂梁的1阶固有频率，并将此频率与无压电片时的固有频率(112.1 Hz)相比较，结果见表1。

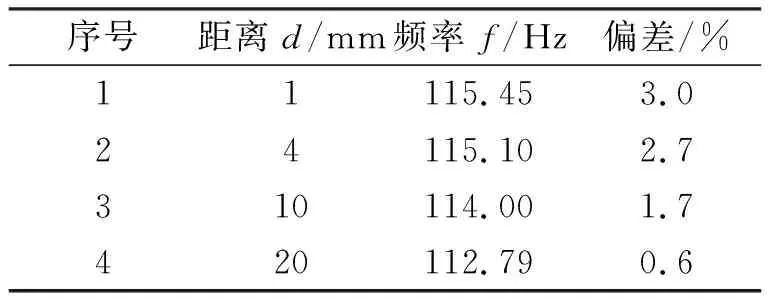
表1 压电片所贴位置的影响

可以看出压电片对悬臂梁频率影响较小，均在3%范围内，压电片越靠近根部，对悬臂梁频率影响越大。所以从力学角度，压电片最好远离根部，但从电学考虑，压电片越靠近根部，应变越大，输出电压也越大，越利于测量。这时，力学的影响与电学的影响需要平衡。

仍以之前的参数为基准，改变压电片的大小，结果见表2。

表2 压电片大小的影响

可见当压电片尺寸变大时，对悬臂梁影响越大，当压电片尺寸接近梁的尺寸时，会带来较大误差，所以压电片应尽量小。

改变压电片厚度，仿真结果见表3。

表3 压电片厚度的影响

可见压电片越薄，压电片对悬臂梁影响越小，但考虑成本问题，一般0.2 mm的压电陶瓷片较易购买，故可使用0.2 mm厚度。

显然压电片尺寸一定时，悬臂梁越厚、越宽、越长，则悬臂梁受压电片影响越小，但有额外因素需考虑：1)过厚的悬臂梁的自由振动频率过高，由于阻尼的存在，振幅衰减较快，不利于测量输出波形；2)从力学理论上讲，增加悬臂梁的长度，使之远大于压电片的尺寸是有利的，但由于压电片有漏电流，频率过低时(比如小于1 Hz)压电片输出电压会减小，不利于测量；3)宽度一般要远小于悬臂长度，否则悬臂梁自由振动时一些力学近似不成立，需按板来计算，增加复杂程度。

2.2 压电片输出电阻的影响

由于压电片的输出阻抗较大，故后续放大电路必须要有足够的输入阻抗，如果测量系统的输入阻抗较小，信号会大幅衰减，影响信噪比，无法观察到有用信号。一般可以用常见的运放芯片OP07或OP37外接电阻搭建成简单的同相运算放大电路，这样输入阻抗就是运放的输入电阻(与压电片电阻相比可认为是无穷大)，也可以采用仪用放大芯片INA116进行放大，电路都简单易实现。此实验中，由于压电片输出电压足够，且示波器表笔输入阻抗极大，故直接用示波器观察压电片的电压输出也没有太大问题，可以省去前置放大电路的设计。

2.3 实验装置及过程

将待测杨氏模量的材料制成一根悬臂梁作为测试件，本实验中，悬臂梁尺寸为59 mm × 4.4 mm × 0.39 mm。值得注意的是，由于悬臂梁端部需要固定，有一段长度将会用于夹持，所以在仿真及计算时，按悬臂梁实际露出的尺寸为准，这里为49 mm × 4.4 mm × 0.39 mm。该尺寸不需要严格限定，以实际加工为准，可适当调整，但要求厚度均匀。

使用夹具将悬臂梁端部进行固定。夹具应远重于悬臂梁，且具有足够的刚度，这样才能尽量减小夹具的影响。将一薄压电片贴于悬臂梁根部，压电片与悬臂梁压紧，使用环氧胶DP460进行粘接。压电片厚度0.2 mm，尺寸约为4 mm × 4 mm，位置离悬臂梁固定端约4 mm。压电片电极用极细的引线引出，引线直径约70 μm，引线越细，则引线的质量影响越小。引线连接到示波器表笔。整个实验装置如图2、图3所示。

图2 实验装置示意图

图3 实验装置实物图

给悬臂梁一个初始位移后放开，这时，悬臂梁处于自由振动状态。悬臂梁因振动产生形变，带动压电片产生形变，压电片因压电效应产生电压，此电压大小随着悬臂梁的振动而周期变化，在示波器上出现周期变化的电压波形。当然，由于阻尼的存在，悬臂梁振动幅度会慢慢变小。通过示波器的暂停功能可以冻结当前波形，并测量波形周期，可以多次测量取平均值以减小误差，或者利用示波器的采集功能，将采集的数据传入电脑进行多次拟合得到更准确的值。

测量出悬臂梁的自由振动周期后，就可以计算出自由振动频率，进而用于计算杨氏模量。

2.4 测量误差

实验测得频率f=112Hz，材料密度已事先测得，为7 840 kg/m3。代入式(5)求得杨氏模量为143 GPa。

杨氏模量的测量误差ΔE由密度误差Δρ、长度误差Δl、厚度误差Δh及频率误差Δf组成。

(7)

现假设密度、长度、厚度可以测量非常准确，误差主要来源于频率误差，则有：

(8)

将f=112Hz，ρ=7840kg/m3，l=0.049m，h=3.9×10-4m代入，并认为Δf=3 Hz，则ΔE=7.6 GPa。

若要提高测量精度，一方面要使频率测得更加准确，另一方面，要合理设计悬臂梁及压电片的尺寸，使得悬臂梁的自由振动频率受压电片的影响尽可能小。采用压电薄膜来替代压电片可以减小压电片对悬臂梁的影响，因为压电薄膜可以比压电片做得更薄。但压电薄膜没有压电片容易购买，这是它的缺点。目前一端固定的方式可能也会引入夹持装置的误差，如果夹持装置刚度不够的话，悬臂梁的共振频率会有所降低，应尽可能使用较为稳固的夹持装置。也可以考虑采用悬吊方式，这种方式可以去除夹持装置的影响，但是吊点需要合理选取，应尽量在振动节点处，最好在测量时能够调整，或者吊点能有一定自由移动的空间，这样当结构件振动起来后，吊点能自动移动到节点位置。然而，激励起来就没有像目前这样只需用手拨动方便，而需采用额外的压电片进行振动激励，并引入驱动电路设备。

3 结束语

本文提出了一种测量材料杨氏模量的方法，利用压电片输出悬臂梁共振时的波形得到振动周期，再通过力学公式反推出杨氏模量。此方法适用于大部分材料的测量，但存在的问题是所贴压电片始终会影响待测件的共振频率。通过合理设计尺寸，可以减小误差，但不可能完全去除该影响。通过类似的动态法测量材料杨氏模量目前已有大量学者进行了研究，包括固定方法、激振方法及从试件形状等方面来提升测量精度。然而，本文致力于实现测量的低成本、简单易行，并尽量不使用到昂贵仪器。本方法与一般的动态法测杨氏模量相比，避免了使用激振设备(包含功放、信号发生器等)、拾振器，悬吊装置等一系列设备。在工程上需要快速估计一种新材料的杨氏模量时，非常有效。有时，就连示波器这样的仪器对一些企业来说并不常备，故为了进一步降低测量门槛，可以考虑采购几片运放芯片及电阻搭建前置放大电路，并可以利用电脑麦克风采集并用软件处理振动信号，这些器件与设备比示波器更容易获取。

当然，若不考虑成本因素，仅考虑测量精度的话，可以采用以下方法：1)非接触式的传感器(如激光位移传感器)，可以去除压电片贴于结构带来的共振频率的改变；2)更高速率的数据采集卡，可以在后期更好地拟合波形，得到更精确的振动周期；3)使用激振设备，给结构以持续的激励，这样得到的波形就是稳定的振动波形，而非因阻尼存在而不断衰减的波形，调整激励信号的频率(通常使用信号发生器)，使振动信号达到最大，可以直接得到共振频率。