犹豫梯形模糊算子在多属性决策中的应用

于 倩，侯福均

1.重庆科技学院 工商管理学院，重庆 401331

2.北京理工大学 管理与经济学院，北京 100081

1 引言

近年来，随着社会的快速发展，以及环境的日益复杂，决策的不确定性大大增强，因此模糊多属性决策越来越受关注。自从Zadeh[1]于1965年提出模糊集的概念之后，其逐渐成为处理模糊信息的有效工具。之后，人们又相继提出了模糊集的几种广义形式，包括粗糙集[2]、2型模糊集[3]、区间模糊集[4]、直觉模糊集[5]、区间直觉模糊集[6]等。

在很多现实决策问题中，决策者在做决策时通常在几个可能值之间犹豫不决，并且不同的决策者给出的方案评价值通常是不同的。基于以上情况，Torra[7]给出了模糊集的另一种广义形式，即犹豫模糊集（Hesitant Fuzzy Set，HFS）。犹豫模糊集被提出后，即受到了学者的广泛关注[8-11]。Xu和Xia[12]定义了犹豫模糊信息的熵和交叉熵，并分析了熵、交叉熵和相似度之间的关系。Zhou等[13]根据Hamacher算子提出了犹豫模糊Hamacher加权平均（Hesitant Fuzzy Hamacher Weighted Average，HFHWA）算子、犹豫模糊Hamacher有序加权平均（Hesitant Fuzzy Hamacher Ordered Weighted Average，HFHOWA）算子和犹豫模糊Hamacher混合平均（Hesitant Fuzzy Hamacher Hybrid Average，HFHHA）算子等。针对属性间存在关联的犹豫模糊多属性决策问题，Zhu和Xu[14]将BM算子拓展到犹豫模糊集环境下，提出了犹豫模糊Bonferroni平均（Hesitant Fuzzy Bonferroni Mean，HFBM）算子和考虑元素权重的加权犹豫模糊Bonferroni平均（Weighted Hesitant Fuzzy Bonferroni Mean，WHFBM）算子。Zhu等[15]基于几何Bonferroni平均（Geometric Bonferroni Mean，GBM）和Choquet积分提出了犹豫模糊几何Bonferroni平均（Hesitant Fuzzy Geometric Bonferroni Mean，HFGBM）算子、犹豫模糊Choquet几何Bonferroni平均（Hesitant Fuzzy Choquet Geometric Bonferroni Mean，HFCGBM）算子、加权犹豫模糊几何Bonferroni平均（Weighted Hesitant Fuzzy Geometric Bonferroni Mean，WHFGBM）算子和加权犹豫模糊Choquet几何Bonferroni平均（Weighted Hesitant Fuzzy Choquet Geometric Bonferroni Mean，WHFCGBM）算子。

然而在现实的决策过程中，由于很多决策问题具有模糊性和复杂性，方案的评价值、属性权重以及专家对决策问题的认知等存在着不能完全确定或者难以用定量数值形式来表示的现象，因此基于梯形模糊数[3]和犹豫模糊集[7]，提出了犹豫梯形模糊集的定义。给出犹豫梯形模糊数的运算法则，进而定义犹豫梯形模糊加权平均（Hesitant Trapezoid Fuzzy Weighted Average，HTrFWA）算子和犹豫梯形模糊加权几何（Hesitant Trapezoid Fuzzy Weighted Geometric，HTrFWG）算子，构建犹豫梯形模糊数的得分函数，给出犹豫梯形模糊数的排序方法，并将其应用在多属性决策领域。

2 预备知识

定义1设X为一非空集合，则定义在集合上的犹豫梯形模糊集可用如下形式表示：

定义2 设是三个犹豫梯形模糊元素，且 λ＞0，则其运算规则如下：

定义3设一个犹豫梯形模糊元素为，则 s(h˜)=称为˜的得分函数，其中是˜中梯形模糊数的个数。是在区间[0,1]的梯形模糊数。对于两个犹豫梯形模糊元素和,如果则如果，则对于和的大小，可以用以上方法来进行比较。

基于犹豫梯形模糊集的运算规则，提出了一系列的犹豫梯形模糊集结算子。

定义4设为集合X上的一组犹豫梯形模糊元素，则犹豫梯形模糊加权平均（HTrFWA）算子定义为：

定理1（幂等性） 设为一组犹豫梯形模糊元素，如果任一都相等，如对于所有 j，有，且，则：

证明如果任意 j,h˜j=h˜，有：

定理2（有界性） 设为一组犹豫梯形模糊元素，令其中，则：

证明有则：

3 犹豫梯形模糊集结算子

定理3（单调性）设和n)为两组犹豫梯形模糊元素，如果对于所有的 j(j=1,2,…,n)，存在，则：

证明由于，可得：

然后

定义5设为集合X上的一组犹豫梯形模糊元素，则犹豫梯形模糊加权几何（HTrFWG）算子定义为：

定理4（幂等性） 设为一组犹豫梯形模糊元素，如果任一都相等，即对于所有的 j有˜，且，则：

证明如果任意，有：

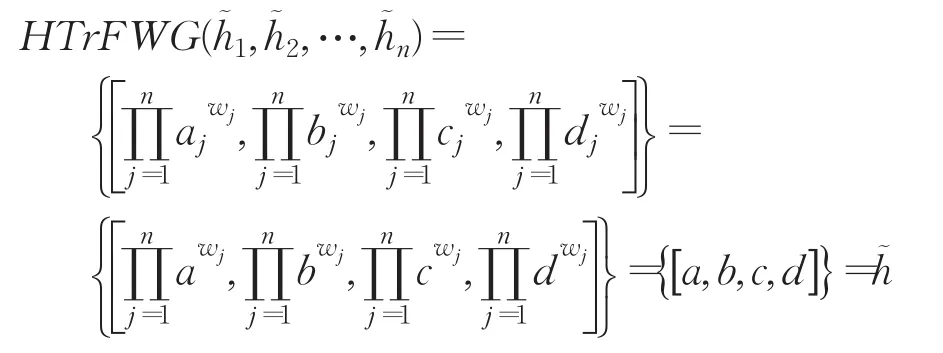
定理5（有界性） 设为一组犹豫梯形模糊元素，令其中a，则：

证明有则：

定理6（单调性） 设和n)为两组犹豫梯形模糊元素，如果对于所有的 j(j=1,2,…,n)，有，则：

证明由于可得：

然后

考虑到犹豫梯形模糊数的有序位置存在具有不同权重的情况，因此定义了犹豫梯形模糊有序加权平均（Hesitant Trapezoid Fuzzy Ordered Weighted Average，HTrFOWA）算子和犹豫梯形模糊有序加权几何（Hesitant Trapezoid Fuzzy Ordered Weighted Geometric，HTrFOWG）算子。

定义6设为集合X上的一组犹豫梯形模糊元素，则犹豫梯形模糊有序加权平均（HTrFOWA）算子定义为：

其中，(σ(1),σ(2),…,σ(n))是 (1,2,…,n)的置换，且对于所有的 j，满足；ω=(ω1,ω2,…,ωn)T是位置权重向量，且

定理7（幂等性）设为一组犹豫梯形模糊元素，如果任一都相等，即对于所有 j，存在˜且，则：

定理8（有界性）设为一组犹豫梯形模糊元素，令其中，，则：

定理9（单调性）设和,n)为两组犹豫梯形模糊元素，如果对于所有的 j(j=1,2,…,n)，有，则：

定义7设为集合X上的一组犹豫梯形模糊元素，则犹豫梯形模糊有序加权几何（HTrFOWG）算子定义为：

其中，(σ(1),σ(2),…,σ(n))是 (1,2,…,n)的置换，且对于所有的 j，满足；ω=(ω1,ω2,…,ωn)T是位置权重向量，且

定理10（幂等性）设为一组犹豫梯形模糊元素，如果任一都相等，即对于所有 j，有，则：

定理11（有界性）设为一组犹豫梯形模糊元素，令其中，则：

定理12（单调性）设和n)为两组犹豫梯形模糊元素，如果对于所有的 j(j=1,2,…,n)，有，则：

从以上定义可知，HTrFWA和HTrFWG算子考虑的是犹豫梯形模糊数本身的权重，而HTrFOWA和HTrFOWG算子考虑的是犹豫梯形模糊数有序位置的权重。这两种算子都没有综合考虑到上述两方面，为了解决这一缺点，定义了犹豫梯形模糊混合平均（HTrFHA）算子和犹豫梯形模糊混合几何（HTrFHG）算子。

定义8设为集合X上的一组犹豫梯形模糊元素，w=(w1,w2,…,wn)T为其权重向量，且则犹豫梯形模糊混合平均（HTrFHA）算子定义为：

定义9设为集合X上的一组犹豫梯形模糊元素，w=(w1,w2,…,wn)T为其权重向量，且是第 j大的加权犹豫梯形模糊元素，且则犹豫梯形模糊混合几何（HTrFHG）算子定义为：

其中，ω=(ω1,ω2,…,ωn)T为位置权重向量，且 ωj≥0，是第 j大的加权犹豫梯形模糊元素，且

4 基于HTr FWA和HTr FWG算子的犹豫梯形模糊多属性决策方法

下面介绍基于HTrFWA和HTrFWG算子的犹豫梯形模糊多属性决策方法的具体步骤。

步骤1.1利用给定的犹豫梯形模糊矩阵和HTrFWA算子，计算得出方案Ai的综合犹豫梯形模糊评价值h˜i(i=1,2,…,m)。

步骤1.2利用给定的犹豫梯形模糊矩阵和HTrFWG算子，计算得出方案Ai的综合犹豫梯形模糊评价值h˜i(i=1,2,…,m)。

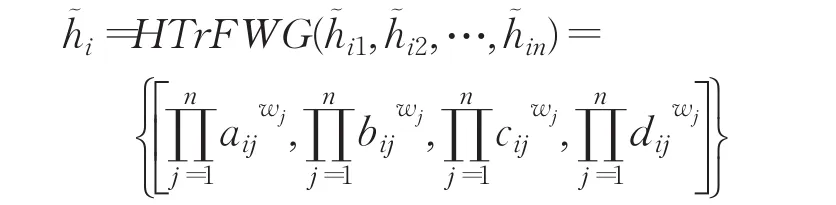
步骤2 计算的得分值

步骤3对进行排序。根据的排序大小，选择相应的最优方案。

5 算例分析

对于一个生产型企业选择绿色供应商问题，假设现有5个绿色供应商Ai(i=1,2,3,4,5)，分别从如下4个属性Cj(j=1,2,3,4)去评价：C1产品竞争力，C2合作与发展潜力，C3供应商竞争力，C4绿色绩效。w=(0.2,0.4,0.1,0.3)T是其权重向量。专家给出各个备选绿色供应商在上述4个属性下的评价值，以犹豫梯形模糊集的形式表示，各个属性评价值构成如下犹豫梯形模糊决策矩阵

为了选择最优供应商，利用犹豫梯形模糊加权平均（HTrFWA）算子和犹豫梯形模糊加权几何（HTrFWG）算子来解决基于犹豫梯形模糊集环境下的绿色供应商评价问题。具体步骤如下：

步骤1.1利用HTrFWA算子将所有的犹豫梯形模糊信息集结成综合犹豫梯形模糊值为例：

步骤2计算综合犹豫梯形模糊值的得分值

表1 犹豫梯形模糊矩阵

步骤3根据各个得分值的大小，对各个供应商进行排序，，因此最优的绿色供应商是A1。

接下来，利用HTrFWG算子来计算各方案的综合犹豫梯形模糊值，步骤如下：

步骤1.2利用HTrFWG算子来计算综合犹豫梯形模糊值以为例：

步骤2计算各综合犹豫梯形模糊值的得分值

步骤3根据各得分值的大小，对各绿色供应商Ai(i=1,2,3,4,5)进行排序，，因此最优供应商仍是A1。

通过以上分析可以看出，虽然利用这两种算子各供应商的最终排序有轻微不同，但绿色供应链中的最优供应商仍是A1。

基于不同算子的排序结果如表2所示。

表2 基于不同算子的排序结果

6 结束语

本文基于犹豫模糊集和梯形模糊数，定义了犹豫梯形模糊集。首先，给出犹豫梯形模糊数的运算法则，探讨犹豫梯形模糊加权平均（HTrFWA）算子和犹豫梯形模糊加权几何（HTrFWG）算子。考虑到犹豫梯形模糊数的有序位置存在具有不同权重的情况，定义了犹豫梯形模糊有序加权平均（HTrFOWA）算子和犹豫梯形模糊有序加权几何（HTrFOWG）算子，并讨论了其相应的运算定理。其次，构建犹豫梯形模糊数的得分函数，并给出犹豫梯形模糊数的排序方法。最后，提出了基于HTrFWA算子和HTrFWG算子的犹豫梯形模糊多属性决策方法，并通过实例进行验证。