基于半监督学习的克里金插值方法

卢月明，王 亮，仇阿根，张用川，2，赵阳阳

1.中国测绘科学研究院，北京 100830

2.武汉大学 资源与环境科学学院，武汉 430079

1 引言

克里金插值法是一种空间最优线性无偏估计方法，是基于空间属性在空间位置上的分布情况，利用半变异函数确定周围待插值点的权重以实现待插值点属性的估计[1]。该方法综合考虑了变量的空间结构性与随机性，通过模拟地理现象空间分布的相关性和变异性进行统计分析，因此，克里金插值方法被广泛应用于气象[2]、土壤[3]等领域。然而，李杰等的研究结果表明，无论哪种插值方法，都需要足够数量的样本数据才能保证插值结果准确可靠[4]。

半监督学习是介于监督学习与非监督学习之间的一种学习方式，其学习样本既包括标记样本，又包括未标记样本，既可以利用大量容易获得的未标记样本，减轻标记样本的工作量，又可以利用标记样本获得更高效的学习模型[5]。协同训练是一种半监督学习方法，它利用双视图训练两个分类器来互相标记样本以扩大训练集，以此借助未标记样本提升学习性能[6]。Yang等的实验结果说明半监督协同训练可利用未标记样本辅助训练，提升只有少量标记样本时模型的学习性能[7]。协同训练法在多视图数据上实验效果很好，已在理论上得到证明：当两个充分冗余视图满足条件独立时，通过协同训练可以利用未标记样本把弱分类器的精度提升到任意高[8]。Wang和Zhou证明了协同训练法的充分必要性定理，结果表明，协同训练只关心权值矩阵的性质，而并不在意权值矩阵是否通过多视图得到，这确认了基于分歧的学习方法并不需要多视图，仅要求分类器之间存在适当的分歧，其必要性条件是每个未标记样本在联合图中都与标记样本连通[9]。

近年来，对半监督学习方法的研究，主要聚焦于解决半监督学习中的分类问题，而对半监督学习中的回归问题的研究相对较少，一个主要原因是半监督学习中的聚类假设在回归问题上不成立，且在回归分析中标记置信度的计算也比较困难。对此，Zhou等提出一种协同回归计算方法（Co-training Regression，COREG），该方法基于不同的距离度量或不同的k值产生不同的k近邻回归模型，然后基于预测一致性来选择置信度高的未标记样本进行标记[10]；马蕾等利用SVM（Support Vector Machine，SVM）来建立回归器，实现了基于SVM的半监督回归训练方法[5]；赵阳阳等提出了一种基于半监督学习的地理加权回归方法（Semi-supervised Learning Geographic Weighted Regression，SSLGWR），并分别使用模拟数据与真实数据说明了SSLGWR的预测结果显著优于单纯的地理加权回归方法[11]；赵阳阳等基于协同训练，提出了协同GTWR方法，结果表明协同GTWR的性能相对于使用不同核函数的GTWR均有所提升[12]；马蕾等提出基于SVM协同训练的回归模型，该模型适用于处理大量有输出的输入情况，缓解了使用单一回归模型所造成的错误累加问题，提升了回归模型的泛化能力[5]。综合上述研究发现：半监督学习理论可有效提升模型的精度，广泛应用于样类分类、语音识别等领域，但随着训练的进行，自动标记中的噪音会不断地累积，其负作用不断增大。

在克里金方法建模过程中，标记样本数据量的多少直接关系到模型的精度，当标记样本较少时，通常难以构建可靠的模型。而在实际应用中，常常难以获取足够数量的标记样本，如PM2.5浓度观测数据。本文针对克里金模型在样本较少时模型精度低这一问题，提出基于半监督学习的克里金插值方法，即自训练克里金插值模型（Self-Training Kriging，STK）和协同训练克里金插值模型（Co-Training Kriging，CTK），并使用北京地区2017年4月和5月的PM2.5浓度数据进行实验。通过与普通克里金插值方法进行对比实验，以平均绝对误差（Mean Absolute Error，MAE）、均方根误差（Root Mean Square Error，RMSE）作为评价指标来说明模型的准确性。通过以上方法，可获得PM2.5在不同地点的浓度，并实现其属性值从点到面的转变，从而为PM2.5空间分布的预测及可视化提供一种手段。

2 研究方法

2.1 克里金插值

克里金插值作为地统计学的核心，用来估算未采样位置的属性值，其研究对象是区域化变量，是一种最优无偏估计方法。它通过变差函数来量化观测数据的空间相关性，建立函数关系，将标记样本代入函数关系，计算权重系数，从而建立插值模型，进行分析或预测。这里的标记样本是指含有自变量和因变量的样本数据，未标记样本指只含有自变量，不含有因变量的样本数据。

克里金插值法可表示为：

其中，λi为权重系数，表示各空间样本点xi处的观测值Z(xi)对其估计值Zˆ(x0)的贡献程度。克里金插值方法的关键在于求权重系数，权重系数的计算需要满足两个假设条件：

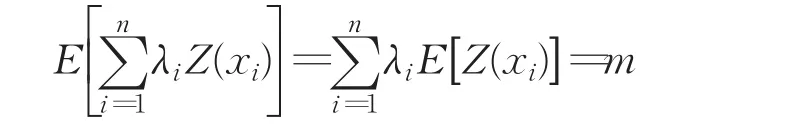
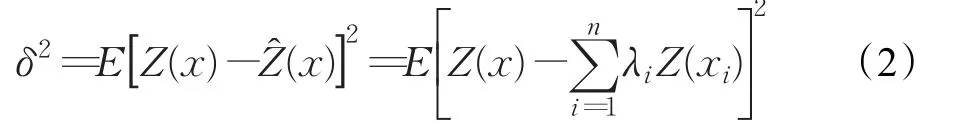
即

通过求解上述克里金方程组，求出权重系数和拉格朗日因子，代入式（1）、（2），即可求出估计值与估计方差。

2.2 半监督学习

2.2.1 自训练克里金模型

自训练方法最早由Fralick等[14]提出，自训练方法是一种半监督学习方法，在每一轮的训练过程中反复运用监督学习方法，将上一轮标记结果最优的样例和它的类标签一起加入到当前训练样本集中，用自己产生的结果不断训练自己[15]。本文将自训练理论应用于克里金插值模型，得到自训练克里金插值模型（STK）。

STK模型的算法流程图如图1所示。

步骤1确定标记样本集、未标记样本集，初始化克里金插值模型参数，该克里金插值模型采用高斯核函数。

步骤2 Kriging模型对未标记样本集进行插值估算。

步骤3从插值结果中选择置信度最高的未标记样本及其预测结果加入到插值模型的标记样本集中，并从未标记样本集中去除该样本。

步骤4重新训练克里金插值模型，直至训练一定数量的未标记样本为止。

2.2.2 协同训练克里金模型

协同训练是一种半监督学习方法，可以在少量有标记样本和大量未标记样本的基础上，通过不断迭代，使得不同学习器互相学习[10]。其原理是建立两个学习器，分别在这两个学习器上使用标记数据与未标记数据，利用学习器和标记数据来标记未标记数据，不断更新另一个学习器的标记数据，通过这样不断互相学习，得到未标记数据的标记，从而扩充标记数据的样本量，提升模型性能[12]。

本文基于COREG算法的理论基础[10]，将克里金插值模型与半监督学习协同训练理论相结合，得到基于半监督学习的协同训练克里金插值模型，即协同训练克里金插值模型（CTK）。协同训练克里金插值模型不仅集成了协同训练在小样本中的独特优势，弥补了样本少的不足，也集成了克里金插值模型在地理应用中的特点。

CTK模型的算法流程图如图2所示。

步骤1确定标记样本集、未标记样本集，初始化两个Kriging模型，两个模型分别为基于高斯核函数的kriging模型和基于指数核函数的Kriging模型。

步骤2每个插值模型对其未标记样本集进行插值估算，从插值结果中选择置信度最高的未标记样本及其插值结果加入到另一插值模型的标记样本集中，并从未标记样本集中去除该样本。

步骤3重复进行步骤2，直至训练一定数量的未标记样本为止。

步骤4最终插值结果为两个插值模型插值结果的平均值。

2.2.3 置信度计算方法

置信度用于从若干未标记样本中选取最优的训练结果，满足预测一致性原则，即具有真实标记的样本应能够体现出插值的内在规律。在模型学习过程中，每一轮选取的未标记样本都会对新插值模型的精度产生影响。基于预测一致性原则选取置信度高的结果，即置信度越高说明越接近真实值。因此，插值模型通过高置信度选择的样本应该是使插值模型与标记样本最一致的样本[16]。本文采用均方误差（Mean Square Error，MSE）作为置信度评判的指标，即如果在未标记样本中存在一条数据，当其加入标记样本集后，使得插值模型的均方误差变小且变小的幅度最大，则这条数据就为置信度最高的未标记样本[10]。置信度计算方法如下：

式中，yL为标记样本的真实值；yˆL为标记样本在原插值模型上的估计值；yˆ′L为标记样本在新插值模型上的估计值，新插值模型是指加入未标记样本后重新构建的插值模型。

当 ξXx∈μ＞0 时 ，令 N(x,u,ν)=arc max(ξXx∈μ) 。N(x,u,ν)即为置信度最高的未标记样本。 ξXx∈μ＞0说明未标记样本的加入使得插值模型性能有所提升。置信度最大说明插值模型性能提升幅度最大，即所选数据是参与训练的未标记样本中置信度最高的数据。

图1 自训练克里金插值模型的算法流程图

图2 协同训练克里金插值模型的算法流程图

3 插值实验

3.1 研究区概况

北京位于东经 115.7°～117.4°，北纬 39.4°～41.6°，中心位于北纬 39°54′20″，东经 116°25′29″，总面积达16 410.54 km2，全市常住人口达2 100多万人，是中国的首都、政治中心、文化中心、科技创新中心。近年来，以PM2.5和PM10为主的大气颗粒物浓度急剧升高，导致北京的雾霾天气频发，以致频频启动“重雾霾橙色预警”。

因此，开展大气污染的相关研究，对掌控空气质量分布状况，采取相关防控举措具有一定意义。

3.2 数据来源

本文选取2017年4月和5月北京地区35个监测站点每小时监测数据，包括 PM2.5、PM10、NO2、CO、SO2、O3等大气污染物的浓度数据，以及每个监测站点的经度与纬度，上述监测数据抓取自网站www.pm25.in。35个监测站点遍布北京城区及其郊县，其覆盖范围基本可以反映整个北京地区的空气质量状况。本文将监测站点按照1∶1的比例随机分成标记样本集（标记监测站点18个）与未标记样本集（未标记监测站点17个）。标记监测站点与未标记监测站点分布，如图3所示。

图3 北京地区空气质量监测站点分布图

3.3 数据处理与校验

首先对每个监测站点每天的24组PM2.5数据求平均得到PM2.5日均值，再由日均值计算出每个监测站点的月均值。然后对监测站点的PM2.5浓度值进行空间数据探索分析，来寻找数据内在的规律性，确定数据是否适合使用克里金插值法。对于不适宜的数据将通过数据变换，使原来不适合于插值的数据可以进行空间插值。由直方图分析得出4月的峰度为3.21，偏态为0.26；5月的峰度为3.04，偏态为-0.57。其中，峰度（Kurtosis）用来描述数据分布的高度，标准正态分布的峰度应为3，峰度值越接近3表示该数据越接近正态分布；偏态（Skewness）用来描述数据左右的对称性，标准正态分布的偏态值应为0，如果偏态值大于0，称正偏态或右偏态，此时大部分数据集中于左边，如果偏态值小于0，称负偏态或左偏态，此时大部分数据集中于右边。北京地区2017年4月、5月的PM2.5浓度Normal QQPlot图如图4、图5所示。

图4 4月PM 2.5的QQPlot图

图5 5月PM 2.5的QQPlot图

通过对监测站点的PM2.5浓度值进行直方图、正态QQPlot图以及半变异函数分析得出，数据很接近正态分布且数据的相关性较高，说明该数据进行空间插值有意义。

3.4 结果与分析

本文将35个监测站点随机等分为2组（标记监测站点集与未标记监测站点集），分别使用普通克里金插值法（Kriging）、自训练克里金插值法（STK）和协同训练克里金插值法（CTK）对未标记站点集进行空间插值分析。为验证模型的精度，通过平均绝对误差（MAE）、均方根误差（RMSE）[17]来对插值结果进行评估。其中平均绝对误差反映估计值可能的误差范围，均方根误差反映插值函数的反演灵敏度和极值效应，这两个指标均是越小代表模型精度越高。经计算，得到3种插值方法的插值精度与精度提升百分比如表1、表2所示。

表1 插值结果精度分析 μg/m3

表2 插值精度提升百分比 %

由表1、表2中的各项指标可知，基于自训练的克里金插值法（STK）相对于普通Kriging法性能没有提升反而有所下降，这种现象是由于早期加入标记样本集中未标记样本的误差在后期训练过程中不断累积放大的结果。基于协同训练的克里金插值方法（CTK）相对于普通Kriging法在4月、5月均有较大幅度的提升，CTK法相对于Kriging插值法（CTK-Kriging）平均绝对误差（MAE）提升程度在10%左右，均方根误差（RMSE）提升程度在11%左右，说明采用两个模型进行协同训练可以有效地削弱早期误差对后期训练的影响，通过合理地利用未标记样本提升了模型的性能。

克里金插值法、自训练克里金插值法、协同训练克里金插值法对北京2017年4月、5月PM2.5浓度的插值结果图如下所示。其中图6、图7和图8为分别使用克里金插值法、自训练克里金插值法和协同训练克里金插值法对北京市4月PM2.5浓度的插值结果图；图9、图10和图11为分别使用克里金插值法、自训练克里金插值法和协同训练克里金插值法对北京市5月PM2.5浓度的插值结果图。

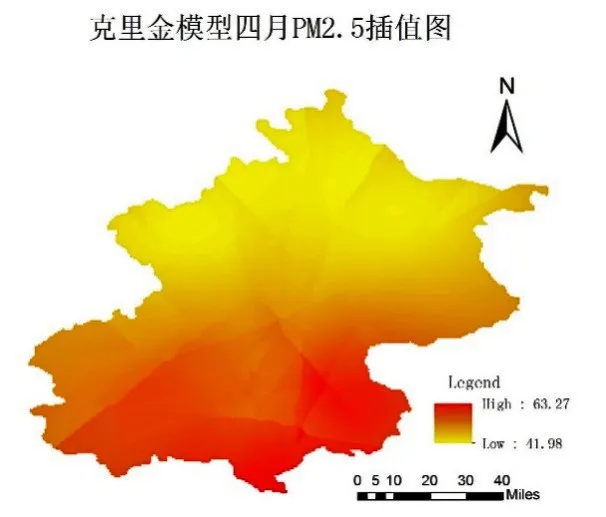
图6 克里金模型4月PM 2.5插值图

图7 自训练克里金模型4月PM 2.5插值图

图8 协同训练克里金模型4月PM 2.5插值图

图9 克里金模型5月PM 2.5插值图

图10 自训练克里金模型5月PM 2.5插值图

图11 协同训练克里金模型5月PM 2.5插值图

由插值结果图可看出5月有较明显的“牛眼”现象。一方面是由于原始测量值中存在奇异值，即孤立点数据明显高于或低于周围监测点数据；另一方面是由于插值区域中监测站点分布不均匀，且插值时将距离作为权重，忽略了方位等其他因素的影响，导致最终结果图中形成以插值点为圆心的圈状现象。此外，5月误差相较于4月略大，也与该数据中存在奇异值有着直接关系。分别对比4月三种方法的插值结果图与5月三种方法的插值结果图可发现，使用自训练克里金方法得到的插值图的颜色均较深，即属性值（PM2.5浓度）均较高；克里金方法和协同训练克里金方法得到的插值图的颜色存在由浅到深的过渡，更符合实际情况，从这一方面也可看出自训练克里金方法的误差相较于另外两种方法偏大。

4 结束语

本文针对数据量较小时，克里金方法插值精度低这一问题，将克里金插值模型与半监督学习理论相结合，利用半监督学习使用未标记样本参与训练来提升回归模型性能的优势，提出了基于半监督学习的克里金插值模型，即STK和CTK。这两个模型既具有半监督学习的优点，适用于解决只有少量标记样本的情况，又可以将离散点的测量数据转换为连续的数据曲面，以便与其他空间现象的分布模式进行比较。本文采用2017年4月和5月北京地区的PM2.5浓度数据进行对比实验，结果表明CTK插值法采用两个协同训练的回归模型，削弱了仅使用单一模型的STK法中错误累积放大的缺点，提高了插值模型的泛化能力。此外，本文未考虑影响PM2.5浓度的因素，如风力、湿度、高程等，未来不仅要在该插值方法上深入研究，还要引入更多的影响因素，以进一步提高插值精度。