基于DNN处理的鲁棒性I-Vector说话人识别算法

王 昕，张洪冉

南京邮电大学 通信与信息工程学院，南京 210003

1 引言

说话人识别[1]也称为声纹识别，是一种基于语音信息实现的特殊生物识别技术。经过几十年的发展，目前无噪声干扰条件下的说话人识别技术已经相对较为成熟。其中，Dehak等提出的i-vector[2]说话人识别方法成为该领域的主流研究技术之一。i-vector方法是在联合因子分析（Joint Factor Analysis，JFA）[3]的基础上发展起来的，能够有效提升说话人识别系统的性能。该算法使用一个低维子空间来表示说话人语音之间的差异性，每段语音被表征成一个固定的低维度矢量（即i-vector）。然而，实际应用环境中，由于加性背景噪声的存在，i-vector说话人识别算法性能会明显下降。因此，如何提高现有说话人识别系统的噪声鲁棒性成为近年来该领域的研究热点。

为解决上述问题，相关研究人员分别在语音信号处理的不同层面做出尝试，旨在不改变说话人相关信息的情况下，降低加性噪声对系统性能的影响。其中，基于频谱分析的语音增强方法作为信号处理前端被引入到说话人识别领域[4-5]。然而，由文献[5]中理论分析和实验结果可以发现，增强后再进行说话人识别的方法能够提高语音信号的质量，却不一定能获取识别性能上的改善。文献[6]进一步证实，在信号处理领域的相关识别算法能否取得好的效果取决于噪声的类型和信噪比的大小。此后，国内外专家学者提出了语音特征领域的说话人识别方法。对于语音来说，特征真实的概率分布依赖于特定的说话人并且是多模态的。然而，在实际应用场景中，信道的不匹配和加性噪声等因素会破坏特征真实的概率分布。相关研究通过将具有噪声鲁棒性的语音特征与均值方差归一化等技术结合，在一定条件下可以调整特征的概率分布，达到降低噪声对系统性能影响的目的[7]。文献[7]中提出的特征弯折算法（feature warping）将训练和测试语音的特征向量的分布映射到统一的概率分布中。经过映射后的特征向量的每一维都服从标准正态分布，在一定程度上补偿了信道不匹配和加性噪声对特征分布造成的影响。但是，对基于不同语音特征的识别算法[8]进行比较可以发现，识别性能是否改善与噪声的类型和信噪比也是紧密相关的。当环境中含有少量噪声时，基于特征域的相关算法考虑到噪声对特征分布特性的影响，通过分布映射等方式调整特征分布可以提高系统的噪声鲁棒性。但是，随着信噪比的减小，噪声影响特征分布特性的同时，也会改变语音中说话人相关的信息，系统性能会急剧下降，通过调整特征分布带来的系统性能上的提升就显得微不足道。

近年来，随着机器学习算法性能的提升和计算机存储、计算能力的提高，深度神经网络（Deep Neural Network，DNN）被应用到语音增强领域中并取得了显著的效果[9-11]。DNN对非线性函数关系具有很强的拟合能力，经过训练后的DNN可以用来表示输入数据和输出数据之间的非线性映射关系。利用DNN的这种非线性结构，通过学习含噪语音特征和纯净语音特征之间的非线性映射关系，将训练好的DNN模型作为一个降噪滤波器来完成对语音的增强工作。文献[12]将DNN作为语音信号前端处理模块应用到说话人识别系统中。但是，上述方法[12]在提高噪声鲁棒性的同时，也增加了系统结构模型的复杂度。

此外，自从i-vector方法引入说话人识别领域后，相关研究人员对直接在i-vector特征空间消除噪声影响做了大量的工作。在文献[13]中提出了纯净i-vector的全方差高斯模型和噪声在i-vector特征空间的概率分布，通过估计含噪i-vector和噪声的概率密度函数，利用最大后验概率（Maximuma Posterior，MAP）方法得到纯净i-vector的估计。DNN也被尝试用来减小i-vector空间中不同类别的说话人的类内协方差[14]。

基于上述研究背景，本文提出将DNN回归模型用于说话人识别系统后端，通过有监督地训练DNN学习说话人含噪语音i-vector和纯净语音i-vector之间的非线性映射关系，得到纯净语音i-vector的一种近似表征。

2 DNN基本原理及其在语音增强中的应用

与传统的人工神经网络（Artificial Neural Network，ANN）相比，DNN具有更多的隐含层数和节点数、更强的非线性函数关系的拟合能力。近年来，基于受限玻尔兹曼机（Restricted Boltzmann Machine，RBM）[15]的无监督逐层贪婪式的参数初始化算法的提出，很好地解决了DNN在学习过程中的局部最优问题，使深度神经网络在各个领域得到了广泛的应用。

2.1 基于受限玻尔兹曼机的参数初始化

RBM是一种两层无向图模型，包含一个可见层和一个隐含层，层间有权重连接，层内无连接。假设RBM的可见层为ν，隐含层为h，( )ν,h的联合概率分布定义如下所示：

其中，W为可见层和隐含层之间的连接矩阵；b和c分别为可见层和隐含层偏置；Z为归一化因子。利用梯度下降和对比散度学习算法，通过最大化可见层节点概率分布P(ν)来获取模型参数。采用自底向上的方法，上一个RBM的隐含层作为下一个RBM的可见层，逐层贪婪式地训练多个RBM，最后将多个RBM叠加可以得到深度置信网络（Deep Belief Network，DBN）[16]结构。将DBN的各层网络参数作为DNN初始化参数，根据学习任务的不同，在DBN最后一层添加softmax层或线性层，可以分别得到DNN的分类模型或回归模型。本文采用线性函数作为输出层的激活函数。

2.2 基于反向传播算法的参数调优

其中，W(l)为l层和l+1层之间的权重矩阵；b(l)为l层偏置；z(l+1)为l层输入值a(l)的加权和；f(⋅)为隐含层激活函数，本文采用Sigmoid函数作为隐含层激活函数。

利用BP算法进行参数调优时，采用最小均方误差（Minimum Mean Square Error，MMSE）函数作为代价函数，通过基于小批量数据（mini-batches）的随机梯度下降算法多次迭代后得到最优值。MMSE表达式如下：

当基于DBN预训练的参数初始化完成后，需要利用误差的反向传播算法（Back Propagation，BP）[17]对DNN网络的参数进行调优。设第0层为输入层，L+1层为输出层，1到L层为隐含层。对第l隐含层，其节点的输出如下：

其中，E表示均方误差；N为小批量数据容量；D为特征维度；Wl和bl分别为l层的权重和偏置参数；和分别表示第n个输入特征样本维度d上的估计值和目标值。对于具有L层隐含层的网络结构来说，当学习率为λ时，权重W和偏置参数b可以通过以下公式进行迭代更新：

需要说明的是，在参数的学习和更新过程中，没有基于网络输入的任何假设，是DNN完全自主的学习过程。

将上述DNN的回归模型结构应用到语音增强中，通过拟合含噪语音特征和纯净语音特征之间的非线性映射关系，利用纯净语音特征的近似表征可以合成得到降噪后的语音。该语音增强方法分为训练和增强两个阶段。在训练阶段，通过将大量的噪声数据和纯净语音相加的方法获得不同信噪比的含噪语音，与相对应的纯净语音一起构成训练数据对并提取相应的语音特征。分别将提取的含噪语音和纯净语音的语音特征作为输入和标签数据对DNN进行训练。语音增强时，直接将含噪语音特征输入，DNN的输出即为增强后的语音特征。在基于DNN的语音增强方法中，没有关于噪声统计特性和噪声与语音之间的独立性等相关假设，这些相关假设往往限制系统性能的提升。此外，大量的训练数据可以保证系统的泛化能力，提高系统的实用性。

3 基于i-vector后增强的DNN鲁棒性说话人识别

3.1 i-vector说话人模型

JFA将说话人和信道的相关变量分别建模成两个不同的子空间，即说话人子空间和信道子空间。然而，文献[18]中相关研究表明，JFA中的信道子空间中也包含有说话人相关信息，分割子空间建模不足够精确。为此，i-vector模型将说话人和信道相关变量统一建模为一个总体变化子空间。该空间同时包含说话人和信道信息，由一个低秩矩阵T表征。在i-vector模型中，不再区分GMM模型均值超向量空间中的说话人效应和信道效应。给定一段说话人语音，包含说话人和信道信息的GMM均值超向量可以表示成如下形式：

其中，m为说话人和信道无关向量，可以用UBM的均值超向量代替；T为表征总体变化子空间的低秩矩阵；w为包含了信道和说话人信息的隐含因子，即i-vector。在i-vector模型中，第i语音段的第t语音帧的声学特征服从以下分布：

其中，ϖk为第k个高斯分量的权重。表征语音段的i-vector即为ω()i的MAP估计。

给定一段语音，通过UBM计算以下统计量：

3.2 PLDA打分模型

说话人识别中的PLDA模型是基于i-vector子空间的因子分析模型。文献[19]指出，简化后的高斯PLDA对不同说话人的i-vector区分性比传统PLDA模型更好。对于给定说话人的R个语音段的i-vector{ωi:i=1,2,…,R}，PLDA模型可以表示如下：

其中，m为所有i-vector训练数据的全局均值；Φ为描述说话人类间差异的子空间矩阵；β为说话人身份相关的隐含因子，服从标准正态分布；εr是服从均值为零，协方差矩阵为对角矩阵Σ的残余项。PLDA模型参数的最大似然估计可以根据文献[20]中描述的EM算法得到。

在系统识别阶段，给定两段语音的i-vector向量，分别用符号η1和η2表示。提出两个假设：

Ηs假设：η1和η2来自同一个说话人，即η1和η2具有相同的隐含变量β。

Ηd假设：η1和η2来自不同的说话人，即η1和η2具有不同的隐含变量β1和β2。

则η1和η2之间的对数似然比可以由以下公式得到：

最后，根据预设的阈值做出最终判决。

3.3 基于DNN后端的i-vector增强

本文在以上研究背景的基础上，提出将DNN回归模型用于对说话人识别系统含噪语音i-vector的增强。当纯净语音受到背景噪声的干扰时，语音的i-vector也会相应地随之发生改变。噪声环境下语音i-vector的改变会导致系统识别性能的下降。含噪语音和纯净语音i-vector之间存在某种复杂的非线性函数关系。因此，本文利用DNN的强大拟合能力，通过训练DNN学习含噪语音i-vector和纯净语音i-vector之间复杂的非线性映射关系，可以得到纯净语音i-vector的一种近似表征。本文使用的DNN模型结构如图1所示。

本文提出的基于DNN的i-vector增强方法分为训练和增强两个阶段。因为DNN的训练为有监督训练过程，数据量的大小和噪声类型的多少直接决定了DNN的泛化能力。因此首先需要构建大量的含噪语音和纯净语音的训练数据对。本文基于加性噪声背景环境，构造含噪语音的方式如下：

图1 用于i-vector增强的DNN模型结构

其中，X为纯净语音；N为噪声数据；α为常量系数，用来控制信噪比。

通过改变噪声的类型和信噪比可以构造出训练DNN所需的大量的训练数据。数据准备完成后，对每一条平行语料，根据第1章所述方法分别提取含噪语音和纯净语音的i-vector，将其最为训练DNN模型的训练数据对，即含噪语音i-vector作为输入数据，纯净语音i-vector作为标签数据。需要说明的是，DNN训练之前，i-vector的预处理操作是必需的。本文对i-vector做了去均值和白化处理。DNN的训练方法和第2章所述一致，即先预训练DBN模型来对DNN进行参数初始化，然后使用BP算法对DNN参数调优。在增强阶段，将训练完成的DNN模型和现有的说话人识别系统模型融合，作为i-vector的特征处理后端，降低噪声对系统性能的影响。需要注意的是，在进行模型融合时，PLDA模型训练和说话人的注册i-vector都需要通过训练的DNN进行特征映射，输出的i-vector再分别用于训练和注册。融合后的系统结构如图2所示。

4 实验设置及结果分析

本文实验环境为Windows 64位操作系统，64位Matlab软件的2016版本。说话人识别模型训练采用微软的Matlab说话人识别工具包[21]。DNN实现部分采用的开源的Matlab深度信念网络工具包（Deep Belief NetWorks，DeeBNet）[22]。

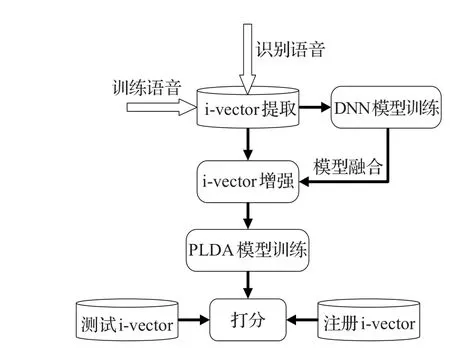
图2 说话人识别系统结构图

本文在TIMIT[23]数据集上进行了实验。采用等错误率（Equal Error Rate，EER）和最小检测代价函数（Detection Function，DCF）作为系统性能评价指标。TIMIT语音库共有630个说话人（192个女性说话人和438个男性说话人），每个说话人10条语音，每条语音平均时长为5 s。从中挑选530个说话人，共5 300条语音，作为UBM和DNN所需的训练数据，100个说话人（30个女性说话人和70个男性说话人）语音作为测试数据，其中，每个测试说话人的9条语音作为注册语音，剩下的1条语音为测试语音，共10 000条测试实验。实验中所使用噪声来自NoiseX-92[24]和freesound（www.freesound.org）网站，其中4个城市噪声（city）样本，4个街道噪声（street）样本，4个餐厅噪声（restaurant）样本，4个办公室噪声（office）样本，2个图书馆噪声（library）样本，4个工作间噪声（workshop）样本。这些噪声数据和用来训练DNN的语音加到一起构成训练DNN的含噪语音数据，其中信噪比为0～30 dB间的随机数值。将取自NoiseX-92噪声库的人群嘈杂声（babble）、车内噪声（car）和驱逐舰轮机舱（destroyerops）噪声与测试数据混合构成测试数据集。

训练UBM模型使用的声学特征为39维（13维基本特征、一阶、二阶差分的组合）、帧长为25 ms、帧移为10 ms的梅尔频率倒谱系数（Melfrequency Cepstral Coefficient，MFCC）特征。UBM的高斯混合数为512，方差采用对角矩阵形式。i-vector维度为400，PLDA说话人子空间维度为200。

本文采用含噪语音的i-vector作为DNN模型输入，纯净语音的i-vector作为训练标签。由表1实验结果可以看出，当DNN隐含层数及隐含结点数变化时，系统的性能会有一定的差异。当DNN模型有两层隐含层，每层隐含结点数为800时，系统具有最好的表现。因此，本文将DNN的隐含层设置为两层，每层800个结点。

表1 不同隐含层结点数时系统在测试噪声环境下的性能表现

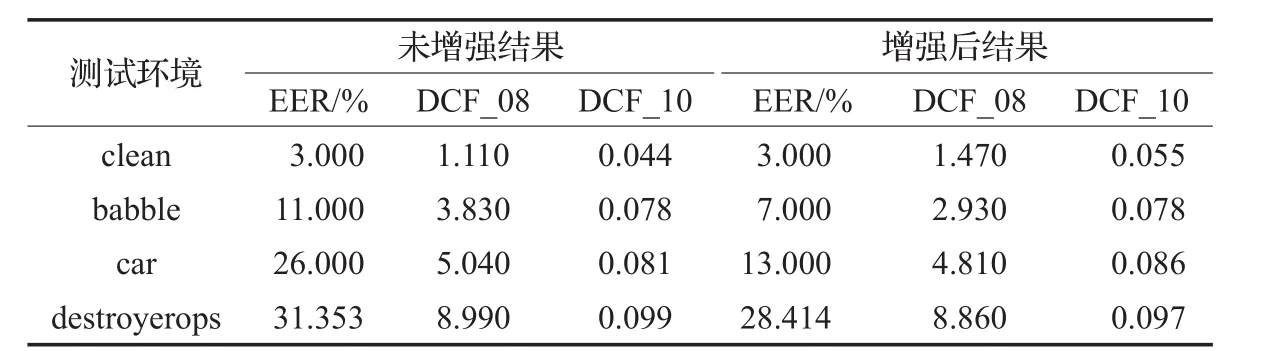
表2 系统在不同噪声环境下的性能表现

表2给出了在纯净语音（clean）、babble噪声、car噪声、destroyerops噪声环境下系统的性能表现。其中，DCF_08和DCF_10的计算方法分别来自美国国家标准与技术研究院（National Institute of Standards and Technology，NIST）2008年和2010年发起的说话人识别评测（Speaker Recognition Evaluation，SRE）[25-26]。

由表2可以看出，系统在不同的噪声环境下性能都有一定的提升。尤其在car噪声下，其EER下降了50%。另外，在纯净语音的情况下，系统在增强前后的表现基本保持一致。

图3到图5分别给出了在不同大小的信噪比条件下babble、destroyerops和car噪声环境下系统的EER折线图。可以明显看出，系统在不同信噪比的噪声环境下都能有稳定的表现。

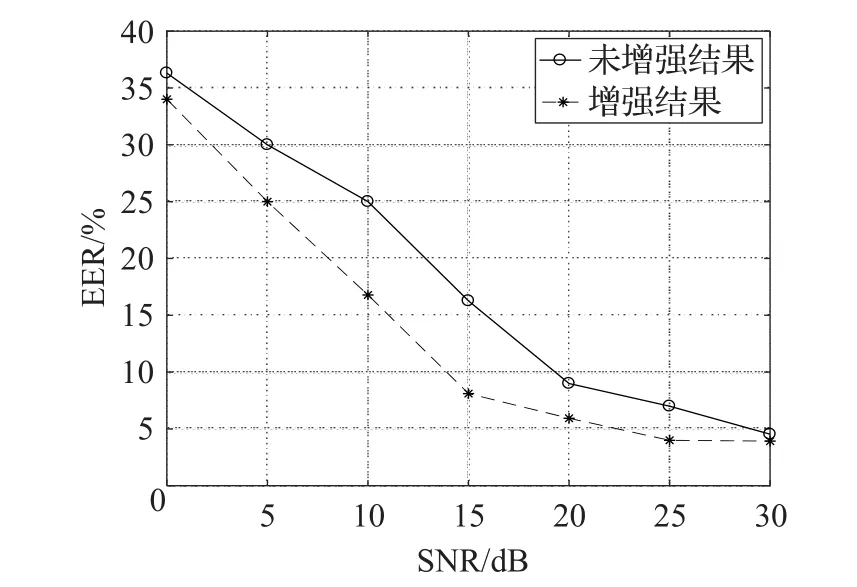
图3 不同信噪比babble噪声下系统EER折线图

图4 不同信噪比destroyerops噪声下系统EER折线图

因为本文信号与噪声的信噪比是随机加入的，表2能够说明在训练和测试环境信噪比不匹配的情况下，系统也具有一定的自适应性。此外，DNN的强大的拟合能力是以大量的训练数据对做基础的，本文只是在较少的噪声环境下做了验证性实验，可能会在某些噪声环境下系统性能并不理想，出现自适应差的问题。

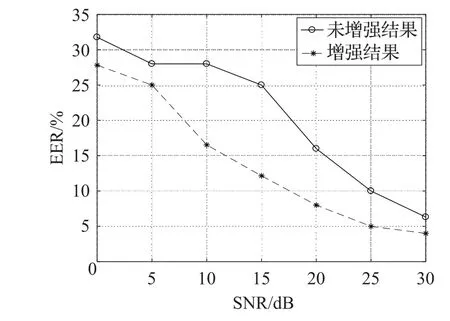
图5 不同信噪比car噪声下系统EER折线图

5 结束语

本文提出一种将DNN用于说话人识别后端对ivector进行增强的方法。该方法首先需要分别提取纯净语音和含噪语音的i-vector。然后用含噪语音i-vector作为输入，纯净语音i-vector作为标签数据训练用于i-vector增强的DNN模型。最后将训练好的DNN模型与说话人识别系统进行融合，得到具有噪声鲁棒性的说话人识别系统模型。本文在TIMIT数据库做的验证性实验证明了方法的可行性和有效性。