基于小波包分析的道岔裂纹定位技术及其应用*

胡锦添 蔡俊涛 刘蓝轩 方恩权

(1.广州市光机电技术研究院，510663，广州；2.广州市智慧感知重点实验室，510663，广州;3.广州地铁集团有限公司，510330，广州//第一作者，工程师)

道岔是城市轨道交通的重要组成部分。由于道岔材质和构造上的原因，机车车辆动载荷的重复作用会使道岔产生疲劳裂纹，裂纹一旦扩展，会使钢轨断裂导致列车出轨[1-3]。现有的轨道检测手段主要是依靠轨道检测车或者超声波探伤车对基本轨进行健康检测，但其无法对道岔这种复杂截面形式的轨道进行准确探伤[4-5]。因此，目前对于道岔检测仍然采用人工方法[6-7]。本文采用声发射Lamb波检测技术全天候实时监测道岔的健康状态，一旦检测到裂纹信号,立刻发出预警信号并对裂纹进行定位。由于道岔是由多个部分组成的，为节省检测设备的制造与安装成本，在道岔的每个组成部分均采用单个传感器实现裂纹检测与定位。

1 裂纹定位原理

1.1 Lamb波频散现象

根据声发射理论，板状结构机械波的传播满足Lamb方程。Lamb波是由无数多个不同阶次的波组成，其传播速度与模态和频率都有关，这就是Lamb波的频散特性。对于板厚远小于波长的薄板，Lamb波主要为不同阶次的对称波和反对称波，通常占主导作用的为最低阶的对称波(S0波，又称为扩展波)和反对称波(A0波，又称为柔性波)。根据板波理论，把相关参数代入方程可求出各阶次波的群速度[8]，这些不同模态导波的群速度曲线统称为频散曲线，如图1所示。

从图1可以看出，反对称波的波速与频率有关，频率越高，传播速度越快。在进行声发射检测过程中，柔性波的幅度相对较高，能量分量较大，所以在定位过程中，到达传感器并超过阈值的时间常常是柔性波的到达时间。但柔性波的波速是随频率变化的，因此要实现相对精确的定位，必须找出同一频率波到达不同传感器的时间差[9]。

图1 道岔中对称波和反对称波的群速度

频散曲线图中并没有显示各种模态波的能量分布，要知道信号在不同时频区间的能量分布，需要借助时频分析工具。可以使用加窗傅里叶变换和小波变换方法。

1.2 单传感器定位技术

常用的声源定位分为区域定位法和时差定位法两大类。其中，区域定位法检测的声源位置为一区域，精确度较低;而最为常用的时差定位法精度较高。一般情况下，将多个传感器按照一定方式分布在薄板的不同位置，根据声源信号到达不同传感器的时间差，经过几何运算,可确定声源的准确位置。但要提高定位精度，则必须准确检测声源信号中同一模态同一频率的声发射波信号。由于道岔钢轨的长度远大于其截面半径，所以道岔声源定位属于一维空间的线定位，一般情况下采用2个传感器进行定位。本文通过单个传感器检测同一模态不同频率的声发射波信号，获得它们的时间差和传播速度并代入式(4),就可计算出声源的位置。道岔声发射源定位原理图如图2所示。其中,cA、cB分别是频率为A的信号和频率为B的信号的传播速度；S为声发射源与传感器的距离。

图2 道岔声发射源定位原理图

频率为A的信号到达传感器的时间为:

(1)

式中:

t——声源信号到达传感器的时间。

频率为B的信号到达传感器的时间为:

(2)

频率为A、B的两个信号的时间差为：

(3)

所以，声发射源与传感器的距离为:

(4)

1.3 小波包分析定位技术

小波变换继承和发展了短时傅里叶变换局部化的思想，同时克服了窗口大小不随频率变化等缺点，能够提供一个随频率改变的时间-频率窗口，是进行信号时频分析和处理的理想工具。为了克服小波分解在高频段的频率分辨率较差、而在低频段的时间分辨率较差的缺点，在小波分解的基础上提出了小波包分解。小波包分解提高了信号的时频分辨率，是一种更精细的信号分析方法。

(1) 小波变换定义。设ψ(t)为母小波函数，则函数f的小波变换为:

(5)

式中:

a——尺度因子;

b——平移因子。

(2) 小波包的定义[10]。在序列空间，存在如下一对递推关系式:

(6)

式中:

wn(n∈N)——由正交尺度函数w0=φ确定的小波包;

hk,gk——分别为低通和高通滤波器系数。

小波系数Wf(ai,bi)是函数f与母小波ψa,b的内积，表示函数f与母小波ψa,b的相似程度;而小波包变换相对于小波变换来说，可通过高通和低通滤波器对高频成分进行分解。若对声发射信号f进行小波分解，与尺度因子ai(i=1,2)对应的信号频率成分到达传感器的时刻为bi(i=1,2)，则信号f的同尺度因子ai对应的频率成分与ψa,b最为相似，表现为Wf(ai,bi)取到模极大值，(ai,bi)为模极大值点[11]。因此，可以通过计算b1-b2的值,获得声源信号同一模态波中两个不同频率成分信号到达传感器的时间差。

2 试验与分析

试验采用长度为15 m的钢轨，在钢轨一端人工制造裂纹缺口，以重物敲击产生裂纹扩展信号，在距离缺口10 m处安装声发射传感器。小波基的选择会对分析效果产生一定影响，为达到理想的分析效果，应选择合适的小波。选择对称小波或近似对称的小波, 以避免相位失真。对于分析典型的声发射信号，本文选用db10小波基[12]。

对声发射信号进行小波包分析时，首先必须确定小波包的分解层数。使用台湾ADLINK高速采集卡DAQ-2010实时采集道岔裂纹声发射信号，采样频率为1 MHz，采样点数为20 000个。根据香农(Shannon)采样定理，其奈奎斯特(Nyquist)频率为500 kHz。通过小波包分析，把声发射裂纹信号分解到第9层，共有29=512个小波包。即把源信号的频域划分为512个子频带，每个子频带的带宽为976.562 5 Hz，其中最低频段为0～976.562 5 Hz，如图3所示。

a) 小波包变换分解树

在判断裂纹信号的过程中，从功率谱密度图分析得知道岔裂纹声发射的敏感频段在100 kHz以上，故结合实际测量结果，选择110 kHz和122 kHz两个频率的分解波作为检测定位信号，其分别位于小波包树第9层中的第113个小波包与第125个小波包。已知轨道板厚度为18 mm，计算可得110 kHz和122 kHz分解波对应的最大速度分别为2 543 m/s、3 812 m/s，其小波包变换后的小波系数如图4所示。

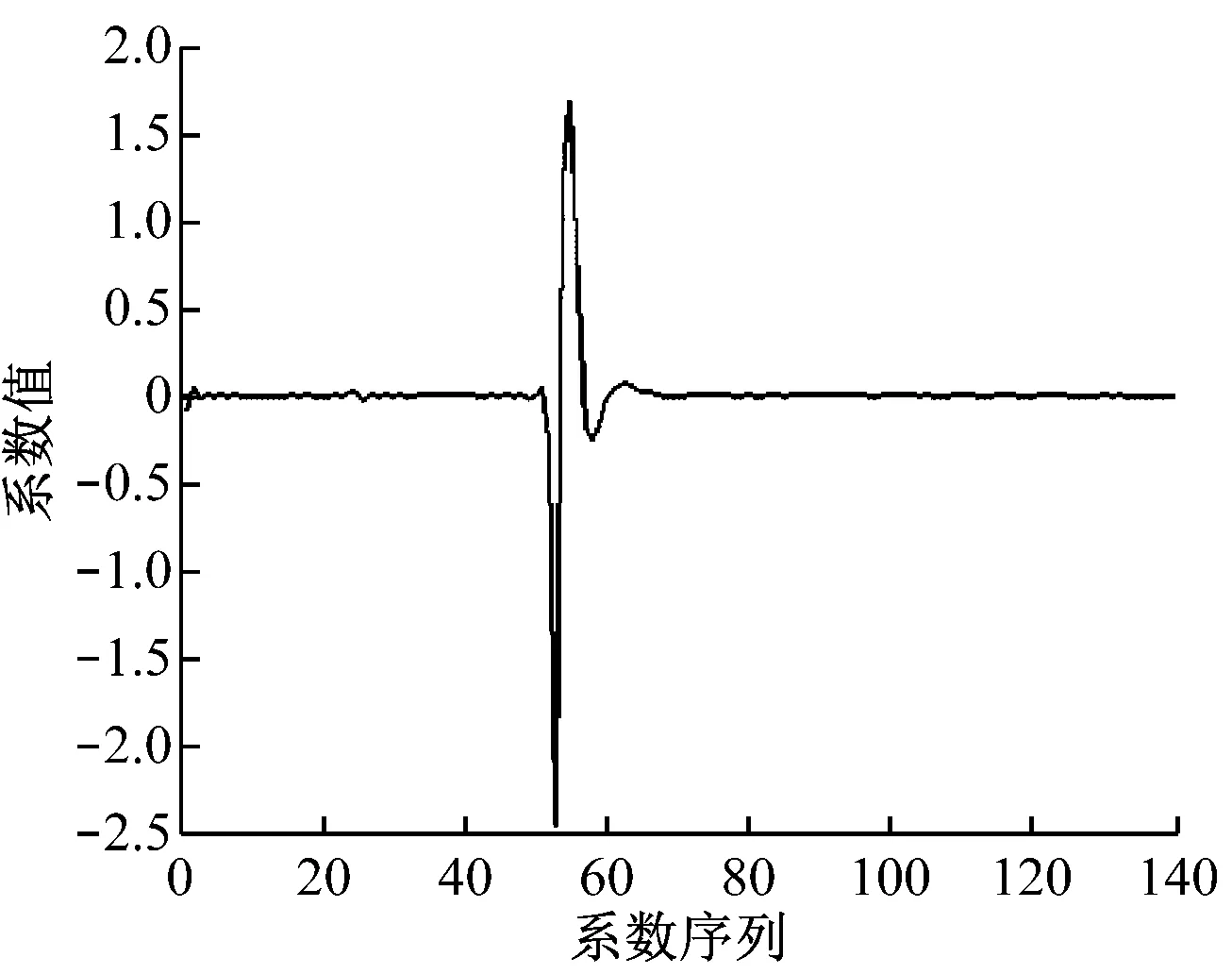
a) 110 kHz附近小波系数图

选取100～180 kHz频段的所有频率进行小波包重构，并绘制成幅值等高线图，如图5、图6所示。通过等高线图纵坐标查找110 kHz与122 kHz两个频率波到达时对应的位置，以Δ标识，找出横坐标中对应的时间，分别为2.44 ms和0.95 ms。两个频率波到达的时间差为1.39 ms，根据式(4)可计算出定位位置为10.62 m。实际裂纹信号位置为10 m。故该方法的定位准确度为93%。

3 结语

本文基于小波包分析对道岔裂纹定位进行研究，采用单个传感器分别检测同一模态下不同频率的Lamb波信号，获得它们到达的时间差即可计算出裂纹的位置。试验证明,该方法定位效果良好。

a) 110 kHz波形图

a) 时域信号

但是,由于受母小波的选择不同、小波包分解层数不够、Lamb波实际传播速度偏差等因素的影响，导致其定位精度不算高，源信号与传感器的距离越大，相对误差越小。在后续研究中，将通过优选适合的母小波进一步提高定位精度。