基于LPP-ELM的微电网超短期负荷预测

马玉鑫

（上海电气集团股份有限公司中央研究院，上海 200070）

0 引言

IT/通信/控制技术是现代微电网运营阶段的核心技术，微电网的建设目标是使终端设备和电网调度互相协同工作，使系统的稳定性、可靠性最大化，同时，使投资和环境影响最小化[1-2]。由于微电网系统规划与运行、收益估算、能源交易等功能都需要依赖精准的负荷预测，所以负荷预测在近年愈发受到人们的关注。根据预测时间间隔的不同，负荷预测被划分为超短期负荷预测、短期负荷预测、中期负荷预测和长期负荷预测，一般的，这四类的分界为一天、两周和三年[3-5]。

因为超短期负荷预测算法执行的间隔短，而且微电网的负荷波动明显大于大电网的波动，这对预测算法的速度和精度提出了双重高要求。在数据积累较理想的情况下，超短期负荷预测应用的算法一般为人工神经网络(Artificial Neural Network, ANN)以及支持向量机(Support Vector Machine, SVM)，其中SVM又因其引入了结构风险最小化的理论，而备受青睐[6-7]。然而，传统的ANN容易陷入局部极值而SVM计算耗时较长，在微电网负荷预测的实际应用中均遇到了问题。极限学习机(Extreme Learning Machine, ELM)是一种结构简单的单层前馈神经网络，它的计算速度快，泛化性能优秀，已经被应用于电力负荷分析与预测[8-11]。

直接应用ELM确实可以有效提高超短期负荷预测的精度，获得了比传统的回归算法更好的预测结果[12-16]。然而，随着微电网系统设备种类增多、结构日趋复杂，采集的测点数和测点种类也在不断增多，而且为了保证监测与控制的功效，采集频率也逐步加快，所以超短期负荷预测模型在训练过程中的干扰因素越来越多，对确保模型精度提出了更高的要求。而且，对于实际工程，影响模型精度的关键因素难以直观辨识，所以仅选取相关性较大的部分变量进行建模，可能会造成预测模型精度较差的问题。但是，如果将采集到的全部变量都用于建模，反而会因维度增大而导致计算复杂度变高，影响模型的泛化能力[17]。

通过引入主成分分析(Principal Component Analysis, PCA)算法消除变量间的共线性特点，然后利用SVM建模，获得了比传统SVM更优秀的负荷预测结果[18-20]。然而，主成分分析的目标是为了将数据方差变化最大的方向保留下来，以此最大限度的“展开”数据，对于服从或接近服从高斯分布的数据集有较好的应用效果。但是，负荷数据具有较强随机性，且电压电流等变量明显不服从高斯分布，所以PCA在负荷数据的特征提取中会丢失部分重要信息[21]。局部保持投影(Locality Preserving Projections, LPP)通过保持局部邻域结构完整，可以克服上述问题的同时，实现特征提取[22]。

为解决电力负荷数据高维度、非高斯的特性造成预测模型精度降低的问题，本文提出了一种基于LPP-ELM的微电网超短期负荷预测算法。首先，选取具有相同天气、温度因素的历史数据作为相似日，并根据负荷数据的时序相关性组成训练数据集，然后，通过LPP进行特征提取，在训练数据的特征空间中利用ELM训练预测模型。最终，通过对某公司实际运行负荷的实验，验证了提出算法的有效性和优越性。

1 局部保留投影

LPP算法通过计算得到一个保持数据局部结构的投影矩阵P∈Rm×P（p＜m），将原始高维空间X=[x1,x2,…,xn]T∈Rn×m转变为低维特征空间Y=[y1,y2,…,yn]T∈Rn×P，其中n 代表数据的样本个数，m和p分别代表X和Y的维度。LPP算法的具体步骤如下：

（1）构建邻接图：根据欧式距离，为X中每个数据xi,xj∈X且i,j=1,…,n，选择距离最近的k个数据点为近邻。若样本点xj属于样本点xi的k个近邻中的任意一个，则在结点i与结点j之间连一条直线。否则，不连线。

（2）计算权重：假设W为待求取的权重矩阵，结点i与结点j之间权重为Wij。若结点之间无连线，则权重值为零。若结点之间有连线，则权重值使用式（1）进行计算：

其中，t为高斯核参数。

（3）特征映射：通过求解式（2），得到特征向量α∈ Rm×m，投影矩阵P∈ Rm×p(p ＜m)为最小的p个特征值λ对应的特征向量：

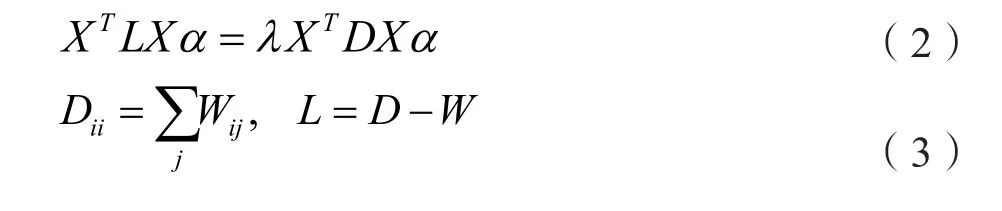
D为对角矩阵，其元素值为权重矩阵的列的和。最后，特征空间的向量可以表示为：

2 极限学习机

ELM是由黄广斌教授提出的一种基于单隐含层前向神经网络的机器学习算法[8]。将LPP提取的特征空间样本的转置为训练样本中的输入，将原始空间中实际的负荷值,… ,t ]∈ R1×n作为输出，隐含层神经元个n数为h，激励函数为g（yT），则标准单隐含层前向神经网络的数学模型为：

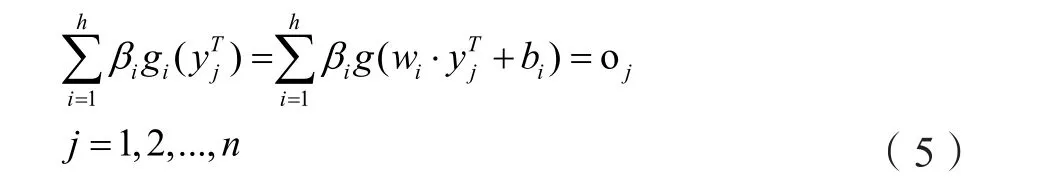
其中，wi是连接第i个隐含层节点与所有输入节点的权值向量，βi是连接第i个隐含层节点与所有输出节点的权值向量，bi是第i个隐含层节点的阈值。wi·yTj表示二者的内积。g（yT）可选为sigmoid、sine或RBF函数等。如要使得该模型能近似表征LPP特征空间，满足则存在βi,wi,bi满足以下等式：

因此，这n个等式可以被写作Hβ=T，其中：

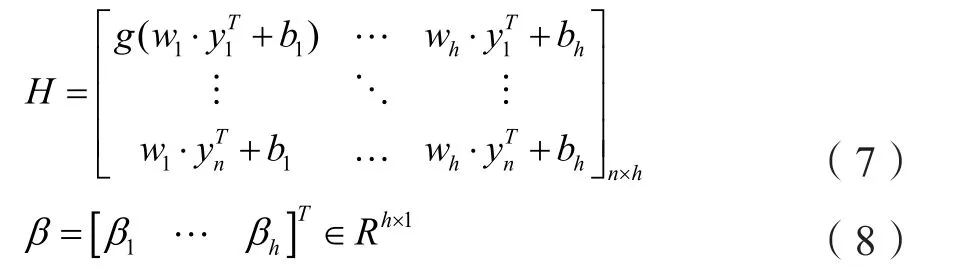
式中H被称为神经网络的隐含层输出矩阵。根据文献[8]所述，式（6）的优化问题最终被转化为：

其中H†是H的Moore-Penrose广义逆矩阵。

3 基于LPP-LM的超短期负荷预测算法

为了解决负荷数据高维度、非高斯的问题，本文提出了基于LPP-ELM的超短期负荷预测算法，其具体流程如下：

（1）根据被预测日的季节类型（第一类包含1、2、12月，第二类包含4、5、6月，第三类包含7、8、9月，第四类包含3、10、11月），匹配选取v天历史数据作为总数据集。

（2）确定负荷预测的参考历史样本点数L，即预测T+1时刻的负荷功率，需要参考T,T-1,…,T-L+1共L个时刻的负荷功率值。

（3）构造LPP算法的输入数据集X=[x1,x2,…,xn]T∈Rv(s-L)×(13+L)，其中s为每天收集的样本数，固定的13列分别为功率因数、电网频率、三相相电流、相电压、线电压、每日最高温和最低温。

（5） 将 标 准 化 后 的 特 征 空 间Y∈Rv(s−L)×p和 负荷 曲 线F ∈Rv(s−L)×1输 入ELM算 法 建 立 预 测 模 型

（6）对被测日数据Xt，首先构造Yt=Xt·P，输入预测模型中，得到T+1时刻被预测值Fp =f( Y tT)。

4 仿真实验

实验数据来源于上海某公司某幢办公楼在2014年7月至2015年6月期间采集的负荷数据，采样频率为5分钟/次，其中负荷数据主要从各电表处获取，而每日天气如最高温、最低温则参考天气预报的信息。

选取ELM算法、PCA-ELM算法与本文提出的LPP-ELM算法进行对比。经过交叉验证，选取特征提取维度p=6，LPP算法近邻个数k=30，ELM隐含层个数h=50，ELM选用sigmoid函数作为激励函数。

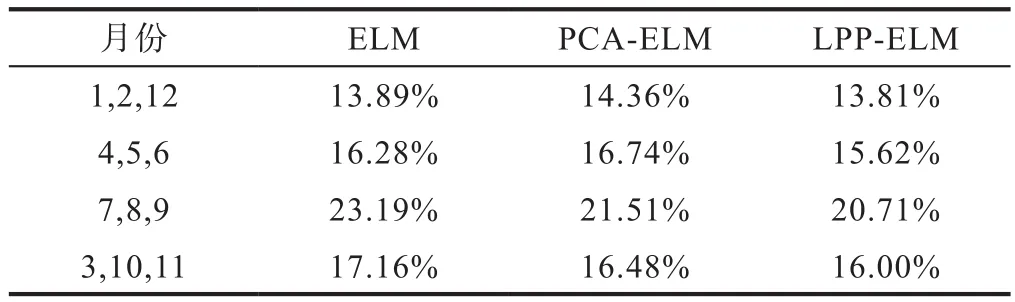
表1 三种算法在不同季节的MAPE值对比Table 1 MAPE values of three algorithms in different seasons

通过表1可以看出，本文提出的LPP-ELM算法在3-11月的负荷预测中，表现均优于ELM和PCA-ELM算法。夏季（7、8、9月）中，三个算法的MAPE值均高于其他季节，原因是夏季空调开启后负荷波动比较剧烈，进行精准预测的难度变大。

通过图1可以看出，2014年10月26日的负荷数据明显不服从高斯分布，由于PCA算法自身的局限性，所以PCA在特征提取时会遗漏部分信息，使特征空间无法完整表达原始数据空间的结构。

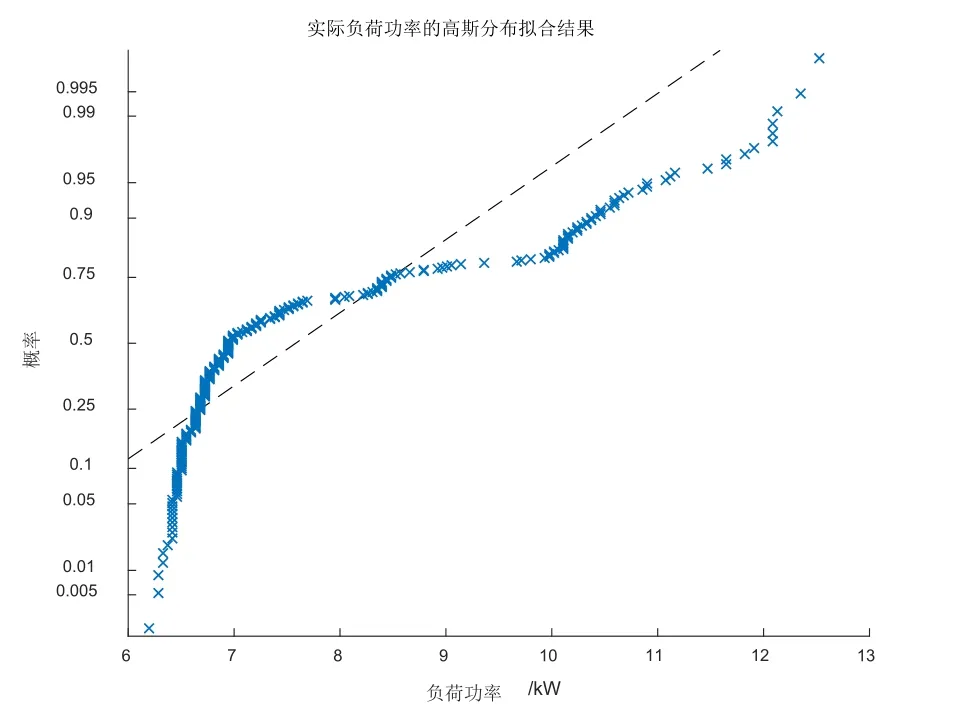
图1 2014年10月26日实际负荷曲线的高斯分布拟合结果Fig.1 The Gaussian distribution fitting result of the actual load data in 2014-10-26

针对上述负荷数据，图2展示了ELM和LPP-ELM预测结果。从曲线趋势可以看出，本日为非工作日，LPP-ELM的预测值可以更好的反映出负荷的波动情况，更接近实际的负荷曲线，所以取得了17.70%的MAPE值，相比ELM小3.09%，此时PCA-ELM取得的结果介于二者之间，为18.73%。

图2 2014年10月26日负荷实际值与预测值曲线Fig.2 Actual and predicted load data in 2014-10-26

图3展示了2015年6月10日的PCA-ELM、LPP-ELM预测值与实际值对比，可以看出两种算法都能较好的预测负荷的波动，但是如图中圈出部分所示，PCA-ELM在部分时刻会出现预测明显失准的情况，其MAPE值只能达到16.77%，而LPP-ELM算法因为在训练建模时通过保持局部邻域结构，克服了数据的非高斯问题，完整表达了负荷数据的特征，MAPE值达到了15.42%。

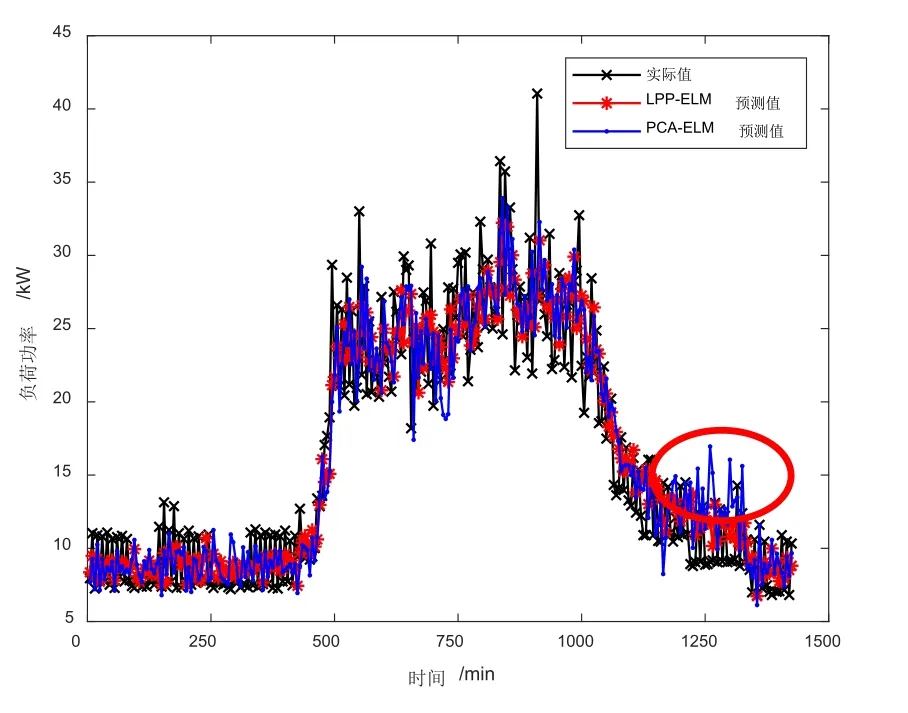
图3 2015年6月10日负荷实际值与预测值曲线Fig.3 Actual and predicted load data in 2015-06-10

5 结论

负荷数据部分变量服从非高斯分布且预测模型的建立需要使用系统的多种被测量。此时直接使用传统ELM算法，模型精度会因被测量中存在噪声干扰而下降。然而先使用传统PCA算法进行特征提取后再使用ELM建模，则会因为PCA的高斯分布假设无法得到满足，导致其特征提取能力下降，最终同样使得建立的预测模型精度降低。针对负荷数据的此种特性，本文提出了一种 LPPELM算法并将其应用在微电网超短期负荷预测中。LPP的引入可以保证由特征提取获得的特征空间信息精度不会因为训练数据包含复杂数学分布而受到影响。最后，通过对上海某公司某幢办公楼的实际负荷数据的实验，验证了LPP-ELM算法的有效性。