领悟典型函数模型 破解大小问题*

广东省广州市第十六中学(510080) 温伙其

中学阶段,有很多常用的函数模型在教材没有详细介绍,它们一般出现在课后习题,如函数f(x)=xlnx出现在人教A版选修2-2(2017年1月第2版)第18页习题1.2,函数f(x)=exlnx出现在人教A版选修1-1(2007年1月第3版)第110页复习参考题,而这些典型函数模型有它特殊的性质,常用于解题.本文介绍八种常见典型的函数模型,并用于解决不等关系的证明,供同行借鉴.

模型一f(x)=xlnx和f(x)=xex

f(x)=xlnx图象如图1,函数在内单调递减,在内单调递增;在区间(0,+∞)上有最小值.

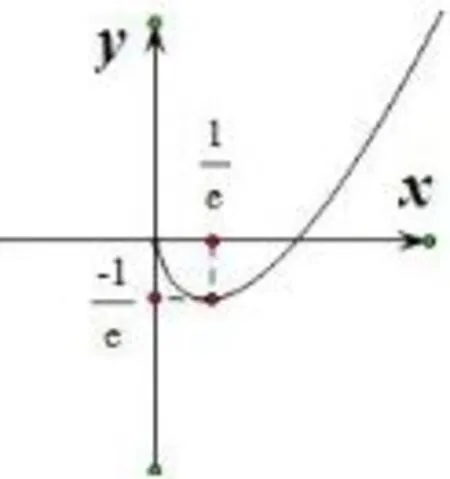
图1

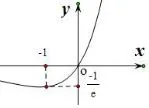
图2

模型应用

例1设函数曲线y=f(x)在点(1,f(1))处的切线为y=e(x-1)+2.

(I)求a,b的值;

(II)求证：f(x)＞1.

思路分析(I)解得a=1,b=2,过程略;

例2已知函数,当a=0时,证明xex≥f(x)在(0,+∞)上恒成立．

思路分析当a=0时,f(x)=lnx+x+1,构造函数F(x)=xex-f(x)=xex-lnx-x-1(x＞0),则,再构造函数g(x)=xex-1,.

f(x)=xex图象如图2,函数在(-∞,-1)内单调递减,在[-1,+∞)内单调递增;在(-∞,+∞)区间上有最小值则g′(x)=(x+1)ex＞0,所以函数g(x)在 (0,+∞)内递增,又因为g(0)=-1＜0,g(1)=e-1＞0,所以存在唯一实数c∈(0,1)使得F′(c)=g(c)=0,且F(x)在(0,c)内单调递减,在(c,+∞)内单调递增,故F(x)≥F(c)=cec-lnc-c-1,又g(c)=0,得cec-1=0,得lnc+c=0,所以F(c)=0,所以F(x)≥F(c)=0,从而证得xex≥f(x)．

模型二

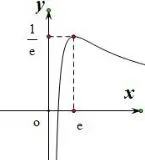
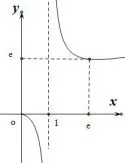
模型应用

例3[1]π为圆周率,e=2.71828···为自然对数的底数．

(II)求e3,3e,eπ,πe,3π,π3这 6 个数中的最大数与最小数．

思路分析(I)由,所以函数f(x)的单调递增区间为(0,e),单调递减区间为(e,+∞)．

(II)根据函数y=lnx,y=ex,y=πx在定义域上单调递增,可得 3e＜πe＜π3,e3＜eπ＜3π,所以这6个数的最大数在π3与 3π之中,最小数在3e与e3之中．由 (I)知,上单调递减,所以即得所以综上可知,6个数中的最大数是3π,最小数是3e．

例4已知函数,．若对于任意x∈(1,e],都有f(x)＞g(x)成立,求实数a的取值范围．

思路分析因为对于任意x∈(1,e],都有f(x)＞g(x)成立,整理得x+(a-1)lnx＞0,即.构造函数,所以F(x)在(1,e]内单调递增,所以F(x)max=F(e)=-e,所以a-1＞-e,即a＞1-e.所以1-e＜a＜0.

模型三

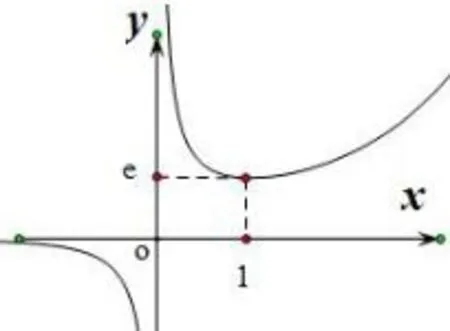
图5

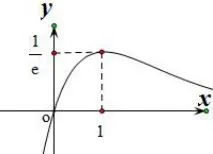
图6

模型应用

例5已知函数f(x)=x2-x,g(x)=ex-ax-1(为自然对数的底数),当x＞0时,f(x)≤g(x)恒成立,求实数a的取值范围.

思路分析当x＞0时f(x)≤g(x),整理得a≤,构造函数,则,再构造函数φ(x)=ex(x-1)-x2+1(x＞0),则φ′(x)=x(ex-2),当x∈(0,ln2)时φ′(x)＜0,所以φ(x)单调递减,当x∈(ln2,+∞)时φ′(x)＞0,所以φ(x)单调递增.又φ(0)=0,φ(1)=0,所以当x∈(0,1)时,φ(x)＜0即h′(x)＜0,所以h(x)单调递减;当x∈(1,+∞)时φ(x)=(x-1)(ex-x-1)＞0,即h′(x)＞0,所以h(x)单调递增,所以h(x)min=h(1)=e-1,所以a∈(-∞,e-1].

例6求证：

思路分析因为x＞0,所以原不等式等价于xlnx＞.构造函数,则当x∈(0,1)时g′(x)＞0,所以g(x)单调递增,当x∈(1,+∞)时,所以g(x)单调递减,所以.再构造函数f(x)=xlnx,同理得,且f(x)和g(x)的最值在不同的x取得,所以f(x)＞g(x),即原不等式成立.

模型四

图7

图8

模型应用

例7已知函数f(x)=ex-a+lnx,若存在x0≥e,使f(x)＜2lnx0,求实数a的取值范围.

思路分析若存在x0≥e,使f(x)＜2lnx0,即ex0-a＜lnx0,整理得构造函数,则再构造函数,有,所以递增,所以所以u(x)＞0在[e,+∞)恒成立,即h′(x)＞0在[e,+∞)恒成立,所以h(x)在[e,+∞)内单调递增,所以h(x)min=h(e)=ee,所以ea＞ee,解得a＞e.

例8当x＞y＞e-1时,求证：．

对本文提出的八种典型函数模型,它们不是孤立存在,而是可以互相转化的,转化过程如下：

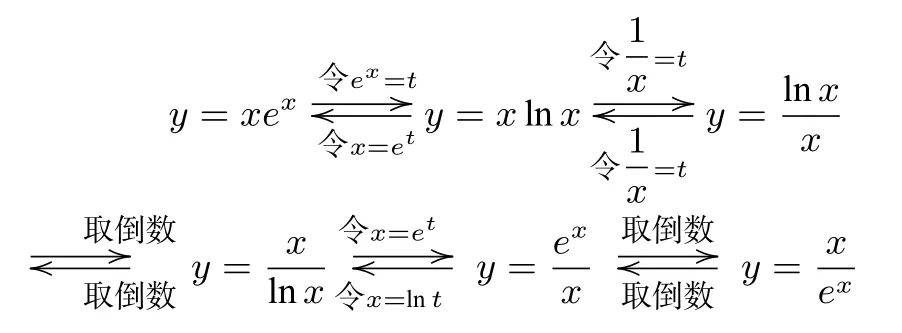
基于此特点,构造模型解题时,思路是双向的,方法是多种的.所以,挖掘教材典型例题、习题,对它们进行深入探究,推广和延伸,则可“源于课本”又“高于课本”.