对函数f(x)=ax+bx+cx单调性的探究及其应用
2018-11-16 05:55安徽省岳西中学246600储百六
中学数学研究(广东) 2018年19期
安徽省岳西中学(246600) 储百六
笔者最近在数学通报2016年第2期上看到如下问题:
问题1(数学通报2285号问题)设a,b,c>0且abc>1,证明:函数f(x)=ax+bx+cx在[0,+∞)上为增函数.
原解答中采用作差比较的方法证明,非常巧妙,不易想到.现在高中已有微积分的知识,用导数判断函数单调性已经是常用方法,下面笔者先将其推广,再通过举例谈谈它的简单应用.
一、问题的推广


二、命题的简单应用
例1设a,b为实数且a+b=1,求证:对任意正整数n,
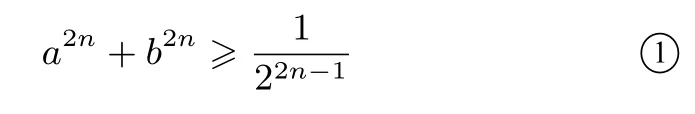
此题为2009年清华大学自主招生试题.文[2-4]中都给出了的证明方法,下面我用命题3给出它的另一证明,然后对其推广
证明(1)若a,b有一个为负数或0时,结论显然成立.
(2)当a,b均为正数但不相等时,,构造函数f(x)=(2a)x+(2b)x,由命题3得函数f(x)在[1,+∞)上为增函数.所以f(2n)>f(1)=2,即(2a)2n+(2b)2n>2,于是.
按此法该命题可轻松推广为:

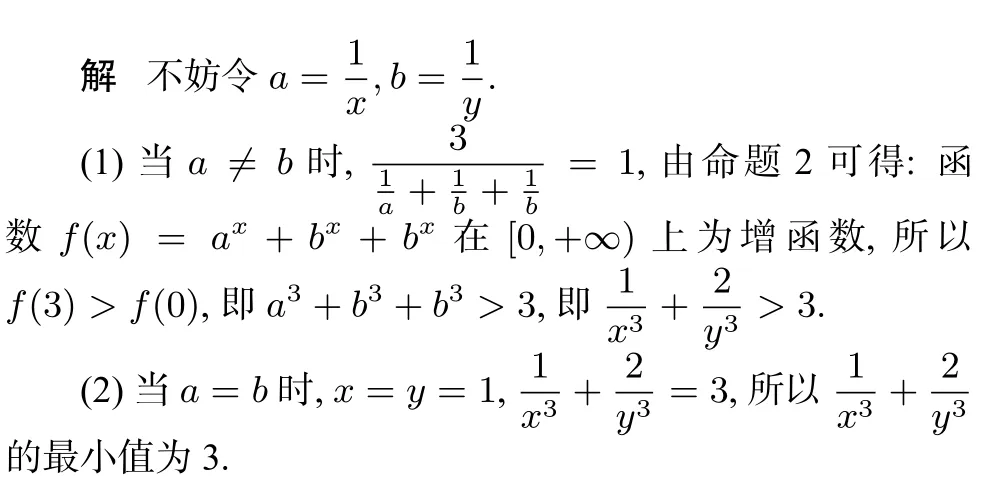
猜你喜欢
轻工标准与质量(2022年4期)2022-08-25
轻工标准与质量(2022年3期)2022-06-29
中学生数理化(高中版.高二数学)(2022年3期)2022-04-26
轻工标准与质量(2022年1期)2022-03-07
轻工标准与质量(2021年6期)2021-12-31
齐齐哈尔大学学报(自然科学版)(2021年2期)2021-03-19
新世纪智能(数学备考)(2021年11期)2021-03-08
新世纪智能(数学备考)(2020年11期)2021-01-04
中学生数理化·高一版(2019年9期)2019-10-12
中学数学杂志(高中版)(2019年2期)2019-04-08

