T型交叉口主路左转远引设置方法及延误研究

张卫华，陈靖生，董瑞娟，陶 虎

(合肥工业大学 汽车与交通工程学院，安徽 合肥 230009)

0 引 言

道路交叉口是多向交通流的汇聚点，如何减少交叉口的车辆冲突和保障行车安全，并提高交叉口运行效率，一直以来是交通工程领域研究的热点问题[1]。道路交叉口中左转车流产生的冲突点最多，如何消除左转冲突国内外学者也开展了很多研究[2]，其中WU J等[3]提出的信号交叉口左转车流借用对向车道(CLL)的交通组织方式，以此来消除冲突并增加左转车流通行能力的方法引起广泛关注；ZHAO Ronglong等[4]通过采集不同路段历史事故数据构建事故率模型，由此确定左转车流远引掉头的位置；近年来国内外学者的研究表明，在交通量较大的交叉口实行左转远引的交通组织方式可以有效减少交叉口交通冲突，提高交叉口通行能力[5-8]。总的来说，目前关于交叉口左转远引的研究主要集中在常规对称十字交叉口，其评价指标也主要以安全和通行能力为主，对远引后车流延误变化研究较少；此外，远引掉头设置方法中往往没有考虑对上下游邻近交叉口的影响。基于此，下面主要研究T型交叉口主路左转车流采用远引掉头的交通组织方法，构建T型交叉口主路左转远引的掉头位置计算模型及其延误计算方法，并分析在不同的交通量下左转车流比例对远引交叉口的延误影响，通过实例的微观仿真来验证方法的准确性和可行性。

1 T型交叉口主路左转远引交通组织分析

1.1 应用环境分析

这里所研究的T型平面交叉口为信号控制交叉口，其两条相交道路分为主路和次路，其中：主路为城市主干道，次路为城市主干道或次干道(如图1，这里将T型交叉口有直行流向的道路称为主路，进口道有左右转流向的道路称为次路，下文均同)。已有研究表明，交叉口设置远引掉头对主路车流饱和度较大时其实施效果更好[9]，且远引掉头开口位置应不能设置于交叉口的功能区内[10]，这就要求远引交叉口与下游交叉口有较大的间距；此外，主路横断面宽度应能满足车辆掉头回转时有足够的换道距离，同时主路还应设有一定宽度的中央分隔带，使之满足主路左转车辆掉头的基本要求。

1.2 交通组织分析

T型平面交叉口主路左转远引如图1，交叉口运行采用两相位信号控制，主路左转与直行为一个相位，次路左转单独一个相位(车辆右转不受信号控制)，其中主路左转远引车流的运行组织过程为：先直行通过交叉口，在主路路段掉头回转到交叉口主路进口道，然后再右转进入次路，实现左转。而慢行交通也采用两相位控制进行组织：次路人行横道相位设置与主路车行相位一致，主路人行横道信号与次路左转车流信号协同控制。主路人行横道较长，可在主路中央分隔带处设置安全岛，使行人安全过街。此外，可在掉头开口处设置掉头和禁止非机动车、行人通行的指示标志来保证远引车辆顺利掉头。T型交叉口主路左转远引后交叉口信号控制由3相位简化为2相位，减少了信号损失时间，从而有利于减少主路直行车流延误，提高交叉口车辆行驶的连续性；同时消除了主路左转车流产生的冲突，也提高了交叉口行车安全。

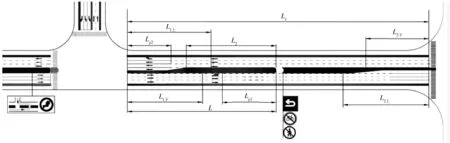
图1 T型交叉口主路左转远引运行示意Fig. 1 Diagram of the operation of T-type interaction of left-turn vehicle

2 T型交叉口主路左转远引掉头位置确定

主路左转远引车流掉头位置、远引车流掉头开口的大小等均是直接影响T型交叉口主路左转远引设置是否合理及其运行效果的关键设计参数，而掉头处开口大小的设置要求，在前期已开展了相关研究，这里不再赘述，具体参见文献[1]。下面重点研究T型交叉口主路远引车流掉头位置的计算方法。

确定远引掉头位置对整个T型交叉口运行起着关键作用[1]。如前所述，设置交叉口主路左转远引的掉头位置不能位于本交叉口功能区内，同样也不应位于相邻交叉口功能区内(文献[1]没有这样的考虑)。如图1，T型交叉口上游功能区长度为L1上,下游功能区长度为L1下，临近交叉口的上游功能区长度为L2上,下游功能区长度为L2下，于是有：

L1-max(L2上，L2下)>L>max(L1上，L1下)

(1)

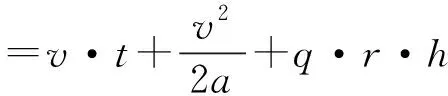
(2)

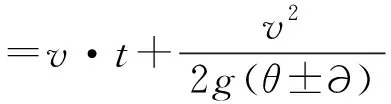
(3)

式中：L为远引车流掉头位置到交叉口的距离，m；L1为T型交叉口与下游交叉口的距离，m；L上表示交叉口上游功能区长度，对应于图1为L1上和L2上；L下表示交叉口下游功能区长度[10]，对应于图1为L1下和L2下；v为车辆的行驶速度，m/s；t为驾驶员感知-反应时间，取2.5 s[11]；a为车辆的平均减速度，取-2 m/s2；q为主路直行车流高峰小时交通量，pcu/s；r为一个信号周期中主路直行相位红灯时间，s；h为车辆停车平均车头间距，m；g为重力加速度，取9.8 m/s2；θ为坡度；∂为汽车轮胎与路面的纵向摩阻系数，实际应用可取0.35。

如文献[1]所述，掉头开口位置到交叉口距离L还应满足车辆回转行驶到交叉口禁止变道线前能换道到右转车道(如图1)，即应满足：

L≥Lp2+L2

(4)

L2=x·La

(5)

式中：Lp2为交叉口禁止变道线长度，设计速度小于60 km/h的交叉口，一般取40 m；L2为车辆想要换道到换道结束所行驶的距离，m；La为强制换道车辆换一个车道平均行驶距离；x为换道车辆数。

下面分析强制换道时的La，强制换道车辆的行驶特性致使车辆即使与前车车头间距逐渐变大，也不急于采取相应措施加速行驶，而是保持一定速度，等待目标车道车头间距大于最小可插入间距时进行换道[1]。因此车辆强制换道行驶距离与目标车道的交通流拥堵程度有关。

通过在交通高峰时间对城市主干路车辆强制换道情况进行调查，以30 s为间隔统计目标车道流率，转换成小时交通量，得到车辆强制换道时目标车道流量与对应的车辆换道行驶距离散点图，如图2(a)。根据已有研究，车辆强制换道时，当目标车道车头时距大于5 s时，大多数车辆可不受影响直接换道。而根据现场调查，目标车道车头时距大于8 s时，车辆均可以直接进行换道，也就是流量小于450 pcu/h时，强制换道距离与目标车道流量关系不大。从图2(a)还可看出流量在450 pcu/h以下时，散点的离散程度较大，这与绝大多数驾驶员的驾驶习惯有关，车辆换道角度一般在4°～10°之间。

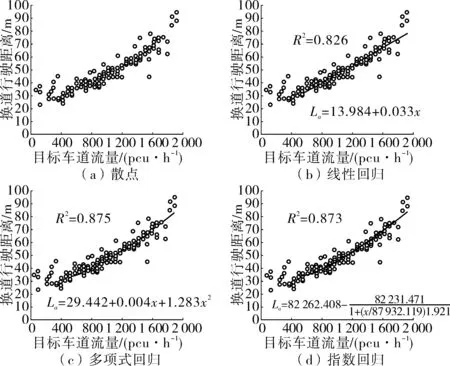
图2 目标车道流量与强制换道行驶距离关系拟合Fig. 2 Fitting figure about the relationship between the target laneflow and driving distance of compulsive lane change

根据散点图的趋势走向，采用origin软件分别选取线性回归模型、多项式回归模型和指数回归模型对目标车道流量大于450 pcu/h的数据进行拟合，得到置信度为95%时，目标车道流量与强制换道行驶距离关系，如图2(b)～图2(d)。可以看出，二次多项式回归模型拟合效果最好，其回归相关系数R2为0.875。因此选择图2(c)中的二次多项式回归模型作为目标车道流量与强制换道行驶距离关系模型，即：

La=29.442+0.004x+1.283×10-5·x2(x≥450)

(6)

T型交叉口远引掉头开口位置L还应大于主路左转远引车辆在掉头口处的最大排队长度Lp1，而由利特尔法则可知，在任何排队系统中，有排队时的平均排队长度为

Lp1=C主左·D排·h

(7)

式中：C主左为主路左转车流在掉头口的通行能力；D排为主路左转车流在掉头口的排队延误。

主路左转车流在中央分隔带掉头可以认为是单通道排队系统，平均服务时间为远引车流掉头通行能力的倒数(简化了文献[1]所提出的计算方法)，则远引车流掉头排队的平均延误为[12]

(8)

式中：x主左为远引车流在掉头口的饱和度，等于q主左/C主左，q主左为主路左转车流流量；β为参数，主路左转车流经过远引路段的行驶，处于自行调整状态，可以认为车流到达服从泊松分布，该参数可取值为1。

主路左转车流在掉头口通行能力的计算，可看成主路优先下次路可穿越的最大交通量，而对向主路车流饱和度较大，车头时距适合用Erlang分布拟合。由此可得到主路左转远引车流在掉头口的通行能力[7]：

(9)

式中：q主为对向主路车流量，pcu/h；k为爱尔朗分布阶数；λ1为主路直行车流到达率，pcu/s；tc为主路左转车流选择掉头时，对向主路车流的可接受间隙，可取6 s；tf为主路左转车流汇入对向车流时的随车时距，一般取3 s。

综上所述，由式(1)～式(9)可知，远引车流掉头位置到交叉口距离L需要满足以下关系：

L1-max(L2上，L2下)>L>max(L1上，L1下，Lp2+L2，Lp1)

(10)

3 远引渠化后交叉口延误计算方法

主路左转车流远引后交叉口的延误包括车辆通过交叉口的信号控制延误、主路左转车流的绕行延误和远引车流在掉头口处的排队延误(如前所述)以及主路左转车流远引时换道交织过程对主路车流产生影响所带来的干扰延误。

3.1 交叉口信号控制延误

T型交叉口主路左转远引后，交叉口信号变为两相位控制，可根据渠化后流量按照常见的Webster信号配时法重新配时，再利用Webster延误模型可得到主路左转远引后交叉口的信号控制延误，即：

(11)

式中：c为信号周期；λi为i相位绿信比；xi为i相位车流饱和度；qi为i相位车流到达流量。

3.2 主路左转车流远引的绕行延误

主路左转车流远引过程产生的绕行延误可分为非交织绕行延误和交织绕行延误(因绕行方式不同于文献[1]中十字交叉口次路远引的模式，所以其延误计算也有差异)。其中，非交织绕行延误是指远引车流从交叉口驶向掉头口产生的绕行延误和远引车流在掉头口换道到右转车道后再行驶到交叉口产生的绕行延误，因此，远引车流非交织绕行延误为

(12)

式中：ε为考虑远引车流的加减速影响，为设计速度的折减系数，实际应用一般可取0.75。

远引车流在掉头口汇入主路车流后需要换道到右转车道，产生换道延误。根据HCM《美国通行能力手册·2010》，可知主路左转远引车流的换道交织为C型交织构造型式，由此可得远引车流与主路车流在交织段的平均速度[13]：

(13)

(14)

式中：Wi为交织车流或非交织车流的交织强度；VR为交织交通量比；q为交织段中的总交通量，pcu/h；n为交织区段车道数；a、b、c、d为标定的常数；Vi为交织段车流的平均速度，m/s；vmax为交织段内车辆可能的最大速度，可取设计速度；vmin为交织段内车辆可能的最小速度，经调查可取4.5 m/s。

所以主路左转远引车流的交织绕行延误为

(15)

由上可得，主路左转远引车流的绕行延误为

(16)

3.3 换道干扰延误

远引车流在掉头口汇入对向主路车流后，变换车道会给主路对向车流带来干扰延误，而使主路车流车速降低[14]。所以主路车流的干扰延误为

(17)

式中：v主为交织段内主路车流的平均速度；qd为受交织影响的主路车流量。

综上所述，由式(12)～式(17)可得远引后交叉口的车辆平均延误为

(18)

4 实例应用分析

按照上文T型平面交叉口主路左转远引的应用环境，以合肥市黄山路-石台路交叉口为例进行分析。黄山路(东西向)路段为双向八车道，石台路(南北向)为双向四车道。交叉口东进口为3个直行车道、一个左转车道；西进口为4个直行车道、一个右转车道；南进口左右转车道各一个。交叉口与下游交叉口距离L1为562 m，主路中央分隔带为7 m,满足大型车在中央分隔带掉头，交叉口高峰小时汽车交通量如表1。

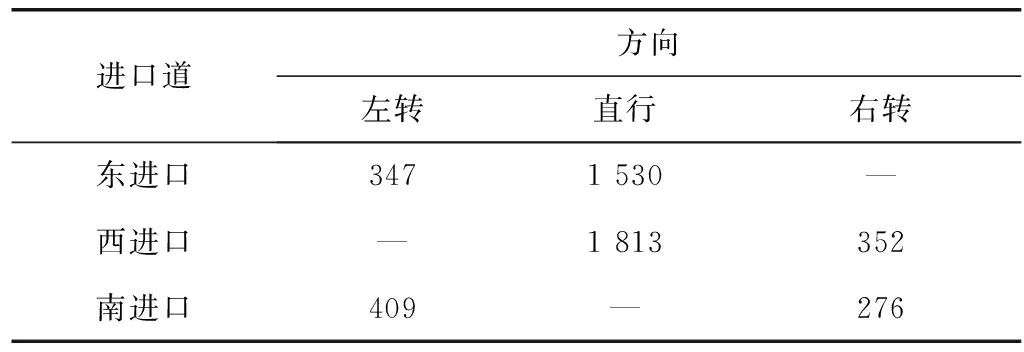
表1 黄山路-石台路交叉口高峰小时流量Table 1 The peak flow of the Huangshan road-Shitai roadintersection pcu/h

交叉口现状采用三相位信号控制，信号周期为90 s。根据高峰小时流量，采用Webster最佳周期优化方法重新配时为103 s。而次路远引后采用Webster信号配时为两相位42 s，其中主路直行相位绿灯为18 s，次路左转相位绿灯时间为16 s，两次黄灯时间分别为3 s，全红时间为1 s。车辆在主路路段运行速度取50 km/h，根据调查车辆平均停车车头间距为8 m。由式(2)、式(3)可得到T型交叉口上游功能区长度L1上为109 m，下游功能区L2上为63 m，下游交叉口的上游功能区长度L2上为126 m，下游功能区L2下为63 m；由式(4)～式(6)可知L>148 m。由表1可得到高峰时交叉口东西向路段流量，用Erlang分布拟合车流车头时距，可得式(9)中分布阶数k取2时，符合x2检验要求；再结合式(7)～式(9)，可得远引车流在掉头口平均排队长度Lp1为16 m。由式(10)可知L取值应大于max(L上，L下，Lp2+L2+Lp1)=148 m，同时应小于L1-max(L2上,L2下)=436 m，这里L取150 m。

由以上求得的结果对交叉口进行渠化设计，把远引掉头位置设置在距离交叉口150 m处，采用前述延误计算方法得到主路左转远引后交叉口车辆平均延误，并和交叉口现状实施三相位的延误以及现状采用Webster最佳配时后的延误进行比较。计算结果表明当交叉口采用主路远引交通组织时延误最小，比现状交叉口采用Webster最佳配时后的车均延误减少49%。利用vissim仿真软件对交叉口采用以上3种不同交通组织方式进行仿真，得到3种组织方式的车辆平均延误如表2，从表2可以看出延误计算值与仿真值相差在6.5 s之内，具有良好的一致性，其结果验证了前述延误计算方法的准确性，也表明了提出的远引交通组织方案适用于该交叉口。

表2 不同交通组织方式下交叉口车辆平均延误比较Table 2 Comparison on average delay of vehicles at different ways of organization intersection

注：D主直表示主路直行车辆平均延误，D主左表示主路左转车辆平均延误，D次左表示次路左转车辆平均延误。

图3 不同左转车流比例下远引前后交叉口延误差值Fig. 3 Difference of delay between front and rear intersection at different left-turn vehicle flow ratio

考虑到不同的左转车流比例和交叉口交通量大小会对远引前后交叉口的延误变化产生影响，以常见的T型交叉口为例，即主路路段为双向六车道，进口道一边为3个直行车道，一个左转车道；另一边为3个直行车道，一个右转车道，次路进口道为左转车道和右转车道各一个。假定左转、右转交通量一样，主路交通量从500 pcu/h，以100 pcu/h为布距增加到1 800 pcu/h，计算左转车流比例分别为主路车流量的15%，20%，25%，3种情形下远引前后交叉口的车辆平均延误差值，其结果如图3。由图3可以看出，T型交叉口主路左转远引可以有效减少交叉口延误，但当主路流量小于1 400 pcu/h时，左转车流比例不同对延误差值影响较小，随着流量逐渐增加，不同左转车流比例下，延误差值变化明显，且显现出左转车流比例越高，延误差值越大，表明此时远引效果越好。

5 结 语

针对T型交叉口主路左转远引的交通组织方式展开研究。建立了主路左转远引时中央分隔带掉头开口位置的计算方法，与以往研究不同的是，综合考虑了远引掉头位置与当前交叉口和邻近交叉口功能区的协调关系；在此基础上，分析了远引渠化后T型交叉口的延误计算方法。通过仿真分析，验证了在一定条件下所提出的T型交叉口远引渠化方法比传统三相位信号控制方法的运行效率更高，能有效减少交叉口车辆平均延误。此外，还分析了不同的左转车流比例和交通量下，远引前后交叉口的延误变化规律，研究表明，主路流量小于一定值时，远引效益不明显，随着流量继续增加，延误差值变化明显，且显现出左转车流比例越高，延误差值越大，远引效果越好。当然，提出的T型交叉口主路左转远引组织方法中，主路只有单边有行人过街斑马线，将会对另一方向进口道行人过街产生不便，因此还需进一步的研究和分析才能作为设计依据。