汽车油箱中油液晃动影响因素的数值分析
张恩慧, 何 仁
(1. 江苏大学 汽车与交通工程学院, 江苏 镇江 212013; 2. 内蒙古科技大学 机械工程学院, 内蒙古 包头 014010)
油液晃动是指汽车燃油箱中油液自由液面的晃动,它是由于部分充液油箱被施加扰动而引起的[1].自由液面大幅度晃动的数值模拟是需要求解非线性非定常的充液系统动力学方程(Navier-Stokes)的初边值问题[2].
对于液体非线性大幅度晃动的研究至今仍被国内外学者关注,主要关于航空、航天、油罐车、载液货船等领域[3-5].综合文献研究可知,很少有学者针对汽车油箱中的油液晃动展开研究.在汽车变工况下,油液在油箱中晃动造成的问题主要分3类:噪声问题[6-7]、油气挥发量增多[8-9]和高变速断油[10].燃油箱中的油液晃动对汽车舒适性、燃油箱排放指标和汽车动力性能均有影响,因此有必要对燃油箱中的油液晃动展开研究,寻找影响晃动的主要因素,为油液晃动的控制提供理论依据.
文中采用VOF法对各种因素影响下的油液晃动进行数值分析,得出油液晃动位置图和各种历程曲线等,并对各种结果对比分析,最后根据分析结果提出防止油液晃动的改进措施.
1 油液晃动方程
研究对象为气液两相流动,采用VOF法进行两相流动追踪.假设充液容器壁面是刚体且不可渗透,液体不黏、不可压缩且无旋,容器做无转动平面运动.图1为惯性及运动坐标系下的充液矩形腔模型.
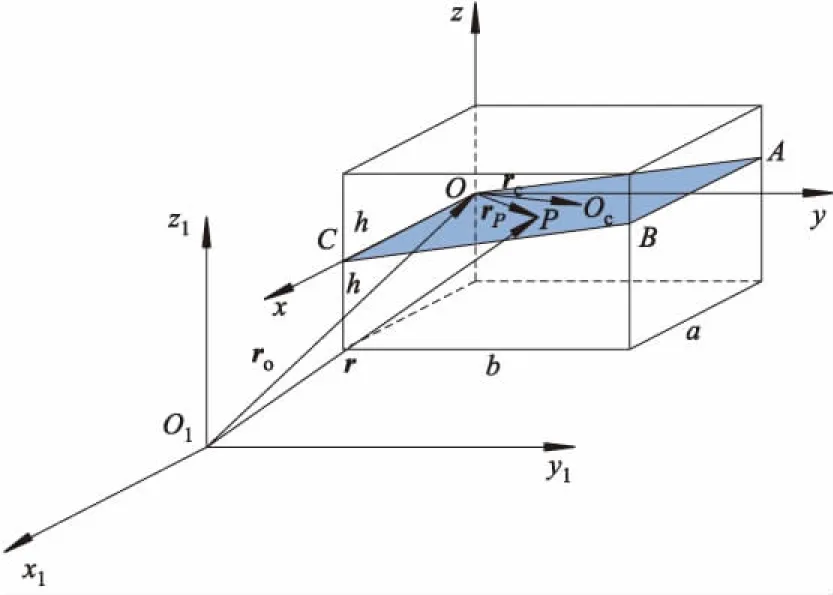
图1 惯性及运动坐标系下的充液矩形腔模型
设充液矩形油箱长为a,宽为b,高为2h.O1x1y1z1为固定的Cartesian坐标系,Oxyz为运动的Cartesian坐标系,z向与2h棱边一致,设O1点为惯性空间中的固定参考点,O点为运动坐标系中的原点,位于棱边2h的中心位置,O1点相对O点矢量为ro,图中阴影部分ABCO为充液矩形腔中的自由液面,组成液面的任意点P相对于O1和O点的矢径分别为r和rP,根据矢量和原理得P点处流体质点的绝对速度:
v=v0+ω·rP+u,
(1)
式中:v,v0分别为P点和O点的速度;矢量rP固结于液体平面ABCO;ω为液体平面的角速度;u为液体的相对流速.
油液在矩形腔体内流动方程为
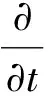
(2)
式中:q为流体速度;∂q/∂t为流体质点的局部加速度;(q·)q为流体质点的对流加速度;为梯度算子;p为流体压力;ρ为液体的密度;gz1为重力场势函数.
(3)
式中:Q为系统的动量;m为系统的总质量(腔体和液体总质量);rc为系统的质点Oc相对于O点的矢径;V为液体容积.
(4)
式中:T为系统的动能;H为系统相对O点的动量矩.
油液晃动受油箱形状约束,而油液与油箱临界面应满足边界条件.设矩形腔壁面函数为F,该函数所满足的边界条件为
(5)
2 矩形充液油箱有限元模型的建立
根据建模准确性和经济性原则,创建矩形油箱的三维几何模型,并在Fluent中VOF模块里创建充液模型,设定油液材料、边界条件和初始条件.图2为矩形充液油箱三维几何模型,容腔容积为40 L,油液高度为5 cm,油液容积为矩形容腔容积的25%.图3为矩形充液油箱有限元模型,采用定尺寸、四面体单元网格,共485 652个.
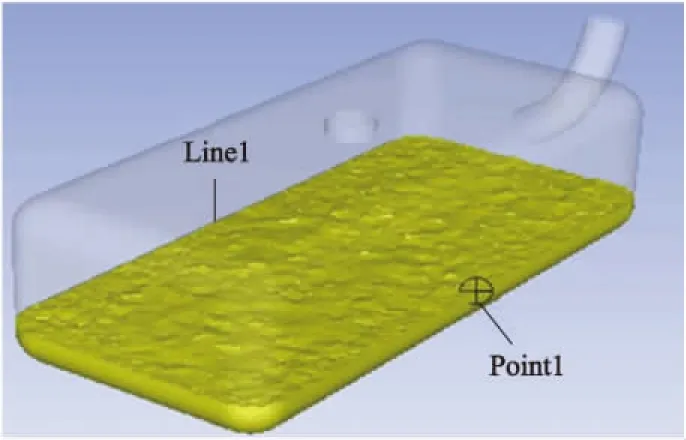
图2 矩形充液油箱三维几何模型

图3 矩形充液油箱有限元模型
3 数值模拟与分析
该模型采用VOF两相流、瞬态和三维数值模拟,通过求解离散方程得到三维耦合压力-速度场,采用格林-高斯节点基数梯度、一阶迎风差分格式动量和一阶隐式瞬态公式等方法.经分析可知,影响油液晃动规律的主要因素有油箱布置方式、充液量、油箱形状、加速度、加速度持续时间和油箱内压力等.
3.1 油箱布置方式
受汽车空间限制,油箱布置方式主要有2种:横向和纵向.通常油箱被固定,与运动汽车之间不产生相对位移,假设油液在横向不产生惯性运动,分别对2种布置油箱中的油液施加前进方向的加速度9.81 m·s-2,在该方向上持续加速度1.5 s后停止,并继续模拟停止加速后1.0 s内晃动工况,油液停止加速度作用后仅受重力作用.
图4为横向布置油箱晃动2.5 s时油液位置图.在0~1.5 s过程中,油液在惯性力和重力共同作用下,在油箱内反复晃动,具有很强的随机性和非线性.图5为油液在纵向布置油箱中晃动2.5 s时油液位置图,2.5 s时大部分油液流动到油箱的右侧.

图4 横向布置,晃动2.5 s时油液位置图
在模型建立过程中,设定相同的初始元素Line1和Point1(图2),横向和纵向布置选择相同元素.图6,7分别为Line1和Point1在横向和纵向油箱布置时,0~2.5 s内平均动压力和总压力历程曲线.

图5 纵向布置,晃动2.5 s时油液位置图
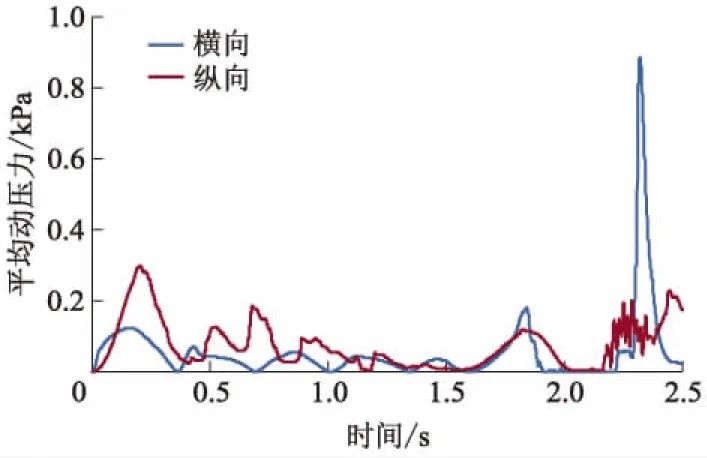
图6 Line1在横向和纵向布置时平均动压力曲线
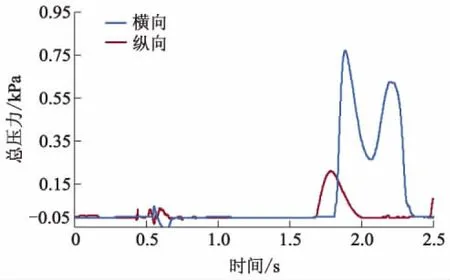
图7 Point1在横向和纵向布置时总压力曲线
从图6可以看出: Line1在0~1.5 s纵向油箱内晃动所受的平均动压力比横向油箱内大;1.5~2.5 s内,由于油液重力势能的冲击导致油液晃动中横向比纵向油箱内所受的平均动压力大.
3.2 充液量
充液量是影响油液晃动的重要参数之一.在相同工况下,分别对25%,50%和75%的充液量进行油液位置模拟.图8,9分别为50%和75%充液量晃动2.5 s时油液位置图.

图8 50%充液量,晃动2.5 s时油液位置图

图9 75%充液量,晃动2.5 s时油液位置图
从图4,8,9可以看出:充液量越少,油液晃动越复杂,75%充液量自由液面基本上处于一个液面高度上.
图10为Line1在不同充液量下油液晃动的平均动压力历程曲线.从整体上可以看出:充液量越多,Line1所受的平均动压力越小,尤其是75%充液量时,油液在0.2~1.5 s时间内所受的平均动压力几乎为0.图11为不同充液量Point1在油液晃动过程中形成的总压力历程曲线,从整体上可以看出,充液量越多,Point1所受的总压力越大,在75%充液量0.2 s时出现压力集中的现象,造成整体油箱所受压力值瞬间升到8.8 kPa,此时极易造成油箱结构的破坏.
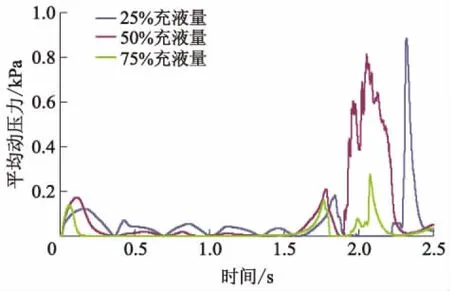
图10 不同充液量Line1平均动压力曲线
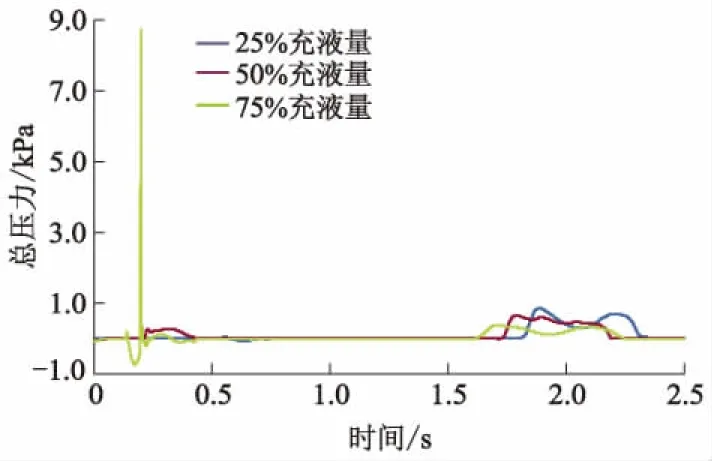
图11 不同充液量Point1总压力曲线
3.3 油箱形状
油箱形状对油液晃动规律有导向作用,也是油液晃动呈现大幅度和非线性波的主要因素.针对矩形和椭圆柱形油箱进行模拟.模拟在油液容积、充液量、横截面积、布置方式和冲击位移量均相同的条件下进行.
图12为椭圆柱充液油箱三维几何模型,同时创建Line1和Point1.图13为油液在椭圆柱油箱内晃动2.5 s后油液位置图,可以看出油液出现了飞溅现象.
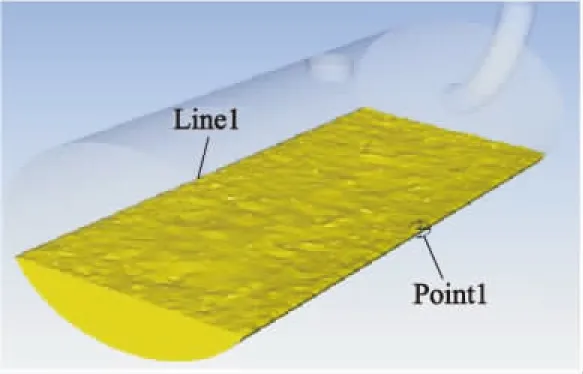
图12 椭圆柱充液油箱三维几何模型

图13 椭圆柱油箱晃动2.5 s时油液位置图
3.4 加速度
在汽车变工况下,油箱中油液随着汽车速度变化而变化,从而形成油液加速度.随着加速度值不同,油液所受的惯性力也不同,因此油液在油箱中的晃动规律也不同,加速度值在汽车制动、加速等工况下一直在变化.
采用的加速度值均为恒定值,在相同加速度工况下,油液具有相同的惯性力和重力势能.图14,15,4分别为加速度值在3.924,7.848,9.810 m·s-2时油液位置图.对比位置图可以看出:加速度值越大,油液晃动液面越高,在加速度为9.810 m·s-2时液面出现了非线性波不规则变形,晃动规律及其复杂.
图16为不同加速度Line1平均动压力历程曲线,加速度值越大,Line1平均动压力越大;最大平均动压力在2.0~2.5 s之间,此时仅重力势能作用.图17为不同加速度下Point1总压力历程曲线.总压力变化的不同之处在0.5~1.0 s和1.6~2.4 s之间;在1.6~2.4 s时,加速度为0.981 m·s-2和3.924 m·s-2时出现了单峰峰值,且最大压力峰值不呈比例,加速度为7.848 m·s-2和9.810 m·s-2时出现了双峰峰值,加速度为9.810 m·s-2时总压力波动较大.

图14 加速度为3.924 m·s-2时,晃动2.5 s油液位置图

图15 加速度为7.848 m·s-2时,晃动2.5 s油液位置图
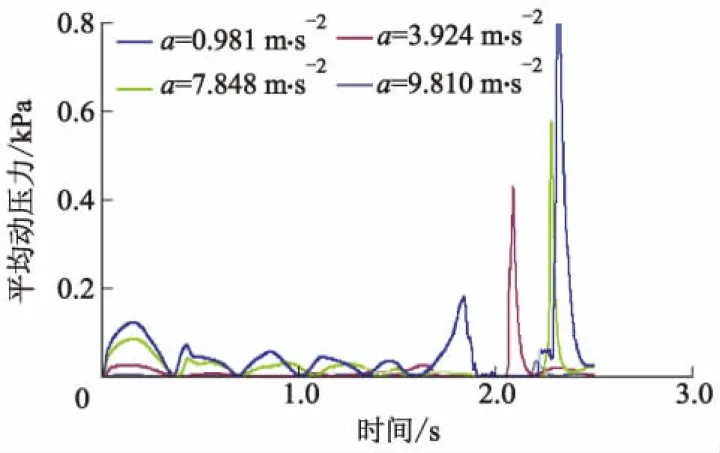
图16 不同加速度Line1平均动压力曲线
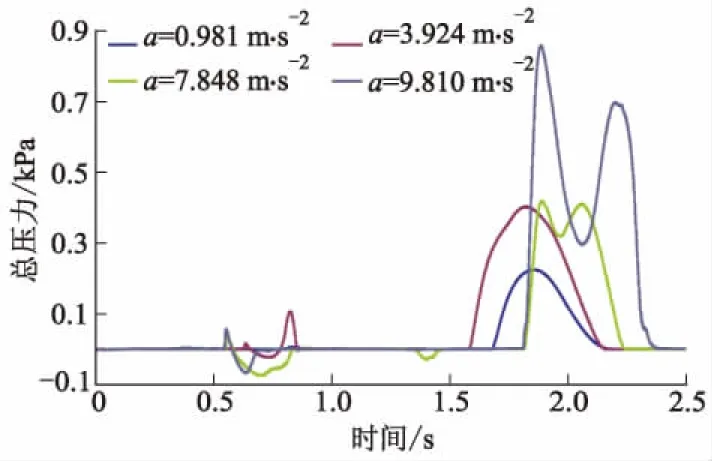
图17 不同加速度Point1总压力曲线
3.5 加速度持续时间
油液加速度的大小决定了油液运动时惯性力大小,然而加速度持续作用时间直接影响油液晃动位置和油液重力势能对油液冲击力大小.
图18为油液在加速度9.810 m·s-2下产生的惯性力和重力共同作用下,晃动1.0 s时油液位置图,此时油液集中在前侧面附近,汽车若加速供油会导致高速断油现象.图19为油液在自身重力势能晃动1.0 s后油液位置图,油液位置呈现高度不平,与图4相比,出现了非线性波变形.图20为不同晃动时间Line1平均动压力历程曲线,加速度持续时间对油液平均动压力有明显影响;油液在2.0 s内晃动的平均动压力比2.5 s时波动大;2.5 s晃动平均动压力比2.0 s时大.图21为不同时间Point1总压力历程曲线,油液加速度停止时间会影响Point1总压力的最大值,并对压力波动形成一定的干扰.

图18 晃动1.0 s时油液位置图

图19 晃动2.0 s时油液位置图
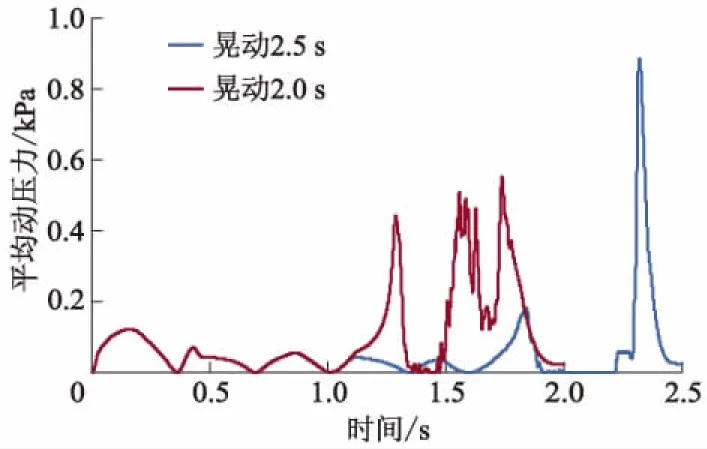
图20 不同晃动时间Line1平均动压力曲线
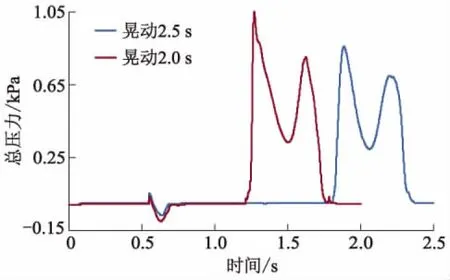
图21 不同晃动时间Point1总压力曲线
3.6 油箱内压力
随着油箱内油气越来越多,导致油箱内的压力升高,油箱压力可以抑制油液晃动,干扰油气分子脱离油液,使油气量的挥发减小.在模拟油液晃动之前,首先在油箱内加设0.1 kPa压力,其余参数不变.
图22为油箱压力0.1 kPa工况下,油液晃动2.5 s时油液位置图,与图4非压力作用相比,油液位置相对平稳.图23分别为0 kPa和0.1 kPa时Line1平均动压力历程曲线,对比曲线可知:油箱内0.1 kPa的压力对Line1形成的平均动压力影响不大.图24为油箱内分别0 kPa和0.1 kPa时Point1总压力历程曲线,油箱内压力为0.1 kPa时Point1产生的负压比没有压力时要大;能降低Point1产生的压力波动,降低效果不明显.

图22 油箱压力为0.1 kPa,晃动2.5 s时油液位置图
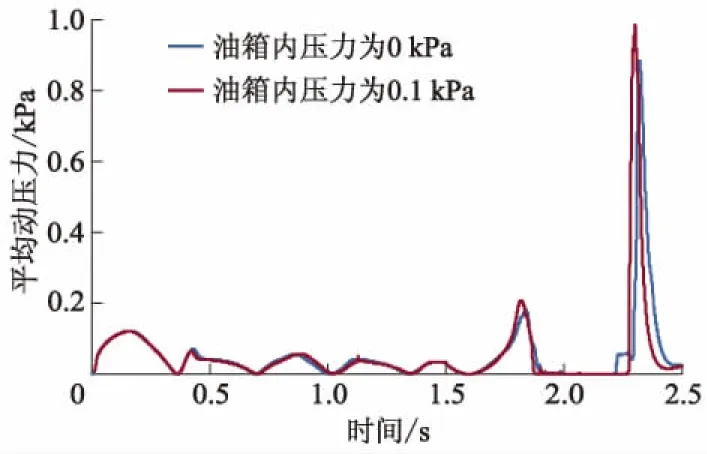
图23 不同压力下Line1平均动压力曲线
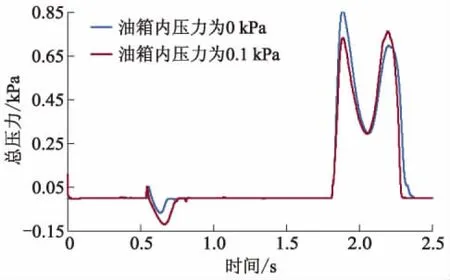
图24 不同压力下Point1总压力曲线
3.7 结果分析及改进措施
3.7.1 结果分析
① 相同条件下,油液在纵向布置油箱内产生的动压力差比横向布置油箱内要小; ② 充液量越多,油液晃动压力越大,在1.5 s时25%,50%和75%充液量所受的最大压力呈等差增长,在2.5 s时最大压力不再呈等差分布,但是增长幅度下降; ③ 与矩形油箱相比,椭圆形油箱可以降低油液晃动的动压力; ④ 油液晃动的加速度值越大,油液在晃动1.5 s时最大压力越大; ⑤ 加速度持续时间对油液晃动幅度和压力有干扰作用,停止时重力势能的大小直接决定后续油液晃动的幅度和压力; ⑥ 随着油箱内的压力升高,油液晃动的压力下降,但是下降幅度不明显.
3.7.2 改进措施
① 在油箱内部增设可移动隔板,对运动的油液进行干扰; ② 在油箱内增设小型吸能机械结构; ③ 根据油箱的晃动规律,对油箱壁面进行优化; ④ 用柔性材料制造油箱,但是该材料必须满足油液侵蚀.
4 结 论
1) 通过比较不同因素作用下的油液晃动数值,得出充液量、油箱形状、加速度持续时间和加速度分别是影响油液晃动动压力、压力波动、重力势能冲击力和最大压力值的主要因素.
2) 非充满油液油箱情况下,充液量越多,油液晃动动压力越大;油液在椭圆柱形油箱内比在矩形油箱内压力波动要小;加速度持续时间决定油液重力势能对油箱冲击力的大小,随机性强;加速度越大,油箱承受的晃动压力越大.
3) 由于在数值分析过程中,模型计算的经济性和准确性不能同时兼得,本研究的网格数属于中型规模,会降低结果的准确性.后续的研究中会不断提高其准确度.

