一种蛇形机器人蜿蜒移动结构设计

白 琨，汪 珺

（合肥学院 机械工程系，安徽 合肥 230022）

1 引言

继德国率先提出“工业4.0”的概念后，美国提出了“工业互联网化”的概念，我国随即也针对性地提出了“中国制造2025”的创新概念.这些变革的背后都体现的一个共同点——实现工业制造的全自动化，机器人的发展将是这场工业变革的重中之重.仿生机器人就是机器人发展的一个重要分支，其中蛇形机器人通过模仿蛇的运动形态和独特的身体结构，以拥有高灵活性、高适应性和高可靠性的特点成为研究的热点.目前，蛇形机器人以实现自重构、自能量、自运动为发展方向[1].

蛇的运动方式主要分为蜿蜒运动、伸缩运动、侧向移动、直线运动、攀爬运动等.机器蛇主要通过电机驱动执行杆件带动各个模块运动、电机直接驱动模块运动、电机改变执行绳索的伸长量等三种方式驱动实现模块间的相对转动，从而实现蛇的各种运动方式[2].本文以蛇类最为普遍的运动方式-蜿蜒运动为出发点，设计一种蛇形机器人机构，为后续开展控制设计搭建平台.

2 serpenoid方程的蜿蜒移动曲线分析

Hirose最早提出了通过观察生物蛇运动曲线得到了serpenoid曲线[3].其方程表达式为

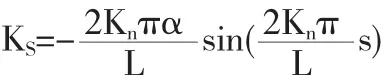
Serpenoid方程可以很好地解释的蛇的蜿蜒运动，可以通过控制方程中的量来控制运动曲线的变化.式中，L表示蛇形机器人的整体直线长度，Kn表示蛇形机器人传播的正弦波的个数，S表示蛇形机器人沿蛇形曲线X方向的位移，α表示蛇形机器人水平线的初始弯角，对Kn进行积分会得到蛇形机器人传递波的波长.图1所示是对Serpenoid曲线的拟合示意图[4]，要想控制蛇形机器人的运动曲线可以通过改变关节之间的转角θi(s)来实现.θi(S)可以通过对Serpenoid方程进行积分得到，计算过程如下：

原式=一式+二式

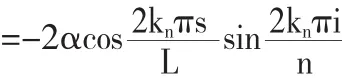
根据二倍角公式，对原式化简得到：

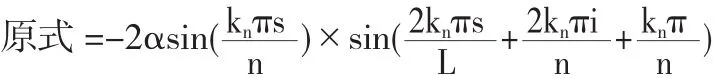
通过θi(S)的表达式可以看出，L是已知量，S可以用带L和θi(S)的表达式来表示，α初始弯角设为零，i是蛇形机器人关节的数量，n表示蛇形机器人传递的波长.所以只要给定n的值就可以控制实现对蛇形机器人的形状控制.

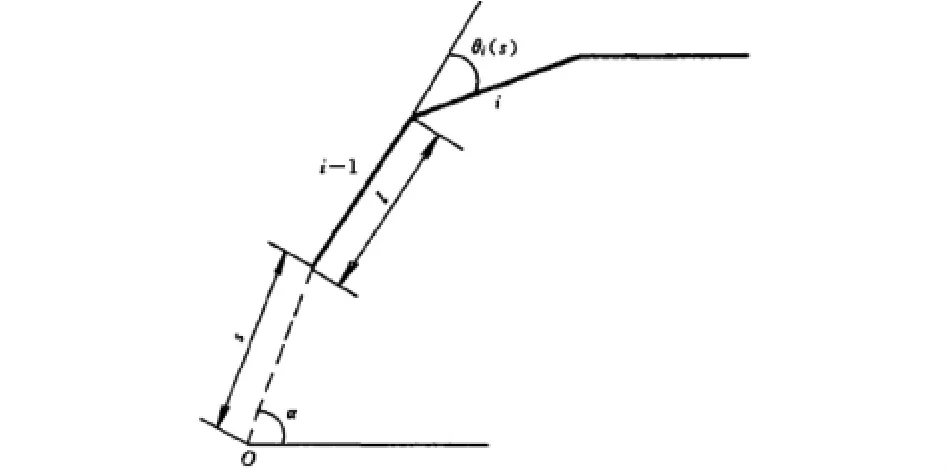
图1 Serpenoid曲线拟合示意图

3 受力分析

根据质点动力学基本方程F=ma，为使设计满足要求的运动速度，需对机器人进行受力分析，以确定机构的质量，进而可以确定机构的尺寸大小.本文从模块化的设计思想出发，将蛇形机器人身体看成是由多个连杆组成的机构.首先对处于水平状态下的单个连杆进行静力学分析，然后对转动 角度的单个连杆进行静力学分析.

3.1 水平状态下连杆的受力分析

图2 水平状态受力分析图

本文只考虑x平面和y平面上所受到的力，图2所示连杆在x平面上受到前一个连杆的作用力F1x，同样在Y平面受到前一个连杆的作用力F1x，此外还受到来自x平面上的静摩擦力f1，连杆所受到的静摩擦力视为全部作用在连杆中间部分，由于连杆处于水平状态，没有向前运动的趋势，所以连杆在水平方向的静摩擦力F1x=0，在竖直方向上的静摩擦力F1x=G×G，其中C是静摩擦因数，G是单元模块的质量.列平衡方程：

3.2 转动后连杆的受力分析

图3所示为转动后水平连杆的受力分析，据图可得下列平衡方程

图3 转动后的受力分析图

通过两个状态下力的平衡方程求解出单元模块的额定驱动力，最终得出蛇形机器人旋转任意角度时地面对单元体的水平反作用力f1x的数学表达关系式：

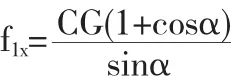
4 结构设计

4.1 模块单元设计

在设计之初，将模块化结构和集成化结构各自的特点进行比较.模块化结构稳定性好，经济性好且便于设计.集成化结构虽然统一性很强，但是集成化结构非常复杂，集成化设计的蛇形机器人动作会很连贯，也会更加灵活.对两种结构方式进行综合考虑，最后选择了模块化结构.首先模块化结构的经济性是选择模块化结构的重要因素，相同的模块所需要的零部件都是相同的，便于制造，另外模块之间的连接方式和连接件也是一样的.模块化结构的稳定性好，由于蜿蜒运动过程中蛇形机器人只受到水平面的摩擦力和地面的支持力，模块单元之间的作用力不受影响，运动稳定性高.模块化结构的容错率也不错，就是当蛇形机器人在运动过程中一个模块出现了问题，整个系统依然可以进行蜿蜒运动.

本文设计了蛇的一个关节，这个关节有且只有水平方向的自由度，关节自带电机，通过自身所带的锥齿轮将电机的转动力矩转换成水平方向左右转动的驱动力，一个关节驱动下一节关节左右转动，多个关节的左右转动就是本文反复提到的蜿蜒运动.通过图4模块单元的三维图可以看出来，锥齿轮是模块的传动件，可以设计一套直齿锥齿轮传动系统作为蛇形机器人模块单元和连接件的传动系统，采用直齿锥齿轮的原因是考虑到模块单元的长度和驱动力大小.表1是蛇形机器人的模块单元参数表[5].

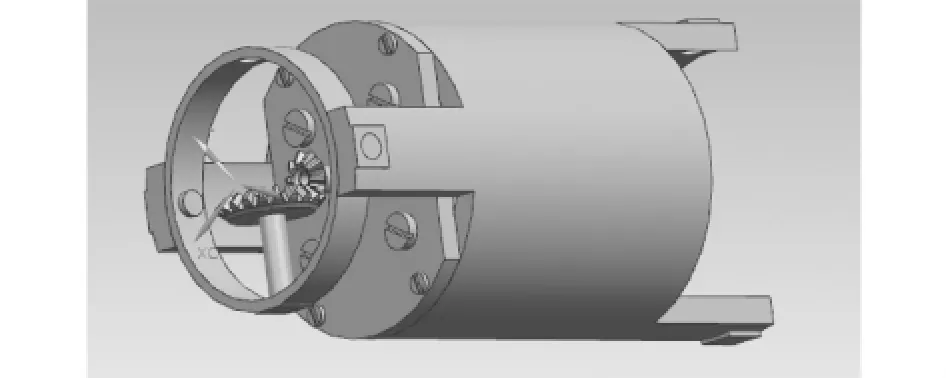
图4 模块单元

表1 蛇形机器人关节参数表

本文设计的蛇形机器人关节与地面是直接接触的，因此摩擦力必然会很大.但是考虑到在关节底部加滚珠会使整个蜿蜒移动系统不稳定，无法控制，所以最终方案没有在关节底部加上滚珠.由于直接与地面接触摩擦力太大，本文考虑后期在关节上包裹一层胶布以减小其摩擦力.由于本文选取的步进电机功率有限，蛇形机器人与地面的摩擦力不宜过大，因为摩擦力的大小跟蛇体的重量成正比，所以本文在设蛇形机器人的时候要着重考虑蛇体的重量.

单元模块设计长度45mm，直径20mm，由圆筒式壳体、步进电机、固定板、大锥齿轮、键等主要零件构成.圆筒式壳体是一个在x方向和y方向都有两个平行的弧形把手的空心圆筒，两边各有一个正交关节的一体式结构；固定板的作用是将步进电机和壳体固定；单元模块与单元模块之间通过环状结构的连接件连接；大锥齿轮通过紧固螺母与连接环固定连接，其作用是传递电机的转动力矩.运动时连接圆环左右转动带动与圆环相连的下一节关节转动.大锥齿轮与圆环是固定连接的，所以大锥齿轮转动和圆环是同时运动的.小锥齿轮转动会带动大锥齿轮转动，圆环就会转动，而下一个关节和环是固定连接，所以下一个关节就会左右转动了.整个运动过程中，驱动马达控制着水平方向的自由度，驱动马达产生了绕自身中心轴线的力矩，通过小锥齿轮转换成单元模块壳体的旋转力矩，此时大锥齿轮又将小锥齿轮的旋转力矩转换成下一个单元模块壳体的转动力矩.通过这样的设计使得蛇形机器人更容易控制，也可以呈现多样的蜿蜒曲线运动.[6]

4.2 模块单元计算

模块单元主要进行锥齿轮传动的设计计算.大锥齿轮通过长螺钉与驱动连接环活动连接，与单元模块上的小锥齿轮是一对直齿锥齿轮传动.[7]连接内环的壁厚是1mm,宽度是4mm，直径21mm，螺钉孔的直径是1.5mm.基本设计要求轴交角∑=90°，小锥齿轮传递的功率P1=20w,转速n1=30r/min，传动比i=2，马达驱动，载荷平稳，单向传动.小锥齿轮传递的转矩，初选载荷系数Kt=1.3，弹性系数，节点区域系数ZH=2.5,齿数比u=i=2, 齿宽系数 øR=0.3，许用接触应力,其中δHim1=310Mpa、δHim2=230Mpa.将上述数据导入分度圆计算公式，得

修正小齿轮的分度圆直径d1=d1t×0.81=17mm.选取小齿z1=20，z2=20×2.5=50.根据啮合齿轮间的关系式算得大锥齿轮的各项数据如下：

多个单元模块（包括连接环）装配后如图5所示.此外蛇形机器人还包括蛇头部分，蛇尾部分.蛇头部分的作用就是在特殊环境下搜集信息，蛇尾部分是完成对蛇体运动方式的控制.

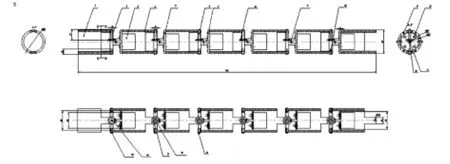
图5 蛇形机器人总装示意图

5 结语

本文对经典的蛇形蜿蜒运动曲线进行了详细的计算分析，确定了单元模块转动角度和蜿蜒形态间的关系，为实现运动控制提供了算法；同时对单元模块进行了受力分析，得出了模块所受力与模块旋转角度之间的关系，从而可确定出模块受力范围，为整体结构的尺寸设计提供了依据.本文最终完成了蛇形机器人蜿蜒运动的结构设计，为后续的控制设计搭建了平台.