基于切比雪夫多项式求解一类分数阶扩散方程

刘建平，杨璐嘉，毛学志

（河北科技师范学院 数学与信息科技学院，河北 秦皇岛 066004）

最近三十年，通过越来越多研究者的努力，确定了在动力学过程中的确具有分数阶性态[1].分数阶导数与整数阶导数相比，它们能够更加精确地模拟自然物理过程和动态系统，它还能模拟物质的记忆和遗传性[3]，因此分数阶微分方程随之成为一种解决复杂数学问题不可替代的数学工具，这就使许多学者开始在各个领域进行分数阶微分方程的研究[2].目前，研究者在求解分数阶微分方程的解析解的过程中，往往通过构造特殊函数，但该特殊函数构造十分复杂，使得求解析解也变得很困难.所以，针对求解分数阶微分方程的数值解的求解方法的研究就显得更加重要了.

分数阶扩散方程是在实际工程中有很广泛的应用的一类方程，一些学者针对该类方程的求解方法展开了研究.文献[4]与文献[5]分别给出了变时间分数阶扩散方程的隐式差分近似和时间分数阶反应扩散方程的全解.文献[6]与文献[7]分别给出了变分数阶非线性扩散方程的一个显式有限差分格式和提出变阶反常次扩散方程的两种值格式；文献[8]与文献[9]分别给出了一个带非线性源项的变分数阶对流-扩散方程的显式和一类变分数微分算子模型的扩散曲线.

笔者考虑到切比雪夫多项式具有良好的正交性质，展开公式中的幂函数数项更容易进行变分数阶微分的计算.因此，从根本上具备了进行函数逼近处理的基础，具有形成算子矩阵的条件.基于以上考虑，笔者探讨利用移位切比雪夫多项式求解变时间分数阶扩散方程的数值求法.考虑的变时间分数阶扩散方程模型[10]如下：

初值和边界条件为u(x,0)=g(x) 0≤x≤1；u(0,t)=h(t)0≤h≤1，其中u(x,t)区间[0,1]×[0,1]上的任意平方可积函数，0＜q(x,t)＜1,f(x,t)已知，u(x,t)未知表示Caputo类型的变时间分数阶导数.

1 预备知识

1.1 Caputo类型变分数阶微分

定义1[11]Caputo类型的变分数阶微分定义

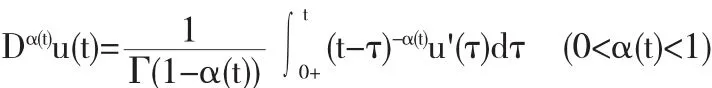
根据定义1，当u(t)=tn时，得到如下的计算结果

其中 0＜q(x,t)＜1.

本文利用了Caputo类型变分数阶微分一些常用性质.

性质1任何常数求α(t)阶导都为零，即Cα(t)=0.

性质2对于任意常数λ,μ，Caputo变分数阶微分算子都有

性质3可交换及叠加性：

1.2 移位移位切比雪夫多项式

切比雪夫多项式[12]定义区间为[-1,1]，一般表现形式为

其在[-1,1]上递推关系为

为了在x∈[0,1]上使用该多项式，作变量替换z=2x-1，得到移位切比雪夫多项式.用Hi(x)来表示，定义如下

此时移位切比雪夫多项式通项可表示为

2 主要内容

2.1 函数逼近

函数y(x)在[0,1]上是可积的，通过移位切比雪夫多项式的变形，有

在实践应用中只需要应用前(m+1)项

其中多项式的系数向量CT和向量函数Φ(x)如下：

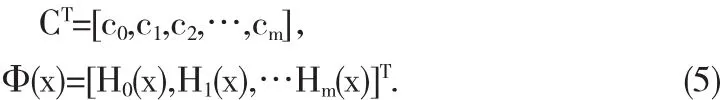
式(4)是根据移位后的切比雪夫多项式(3)得到的y(x)函数近似表示.

对于任意二元函数u(x,t)∈L2([0,1]×[0,1])，都可以通过移位切比雪夫多项式进行函数的近似.一般地，也只对前n+1项作考虑

ui,j(i=1,2,…n；j=0,1,…,n)表示移位切比雪夫多项式逼近二元函数的待求系数，如下

矩阵U用内积表示为U=Q-1〈Φ(x),〈Φ(t),u(x,t)〉〉Q-1.Q，Φ(x)，Φ(t)分别为

2.2 基于算子矩阵求解变时间分数阶扩散方程

本节将推导变分数阶矩阵算子.首先将式(5)表示成为矩阵形式(7)

其中 Tn(x)=[1,x,x2,…,xn]T，

称为移位切比雪夫多项式的系数矩阵.矩阵A为一个上三角形且对角线没有零元素，故可逆，从而有Tn(x)=A-1Φ(x).

对Φ(t)一阶求导，有

其中D为(n+1)×(n+1)阶的矩阵，称为移位切比雪夫多项式的一阶微分算子矩阵.根据式(7)可得

定义如下形式(n+1)×n阶矩阵V(n+1)×n和n维列向量Tn*(t)

由于一元函数u(t)=CTΦ(t)，则可将其导数u'(t)转化为矩阵形式，即

对式(9)求二次导，可得Φ"(t)=D2Φ(t).针对任意的二元函数u(x,t)，对x求二阶偏导都可以得到如下式子：

下面将推导Φ(t)的q(x,t)阶微分矩阵算子

其中

称为移位切比雪夫多项式的q(x,t)阶微分矩阵算子.

利用公式(14)，将Dq(x,t)tu(x,t)表示为矩阵形式，可得

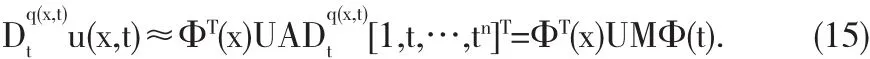
将式(13)和式(15)代入方程(1)中，得到如下形式：

2.3 数值算例

例1 解如下变时间分数阶扩散方程

该方程的精确解是u(x,t)=x2(1-x)(1+t3).

故n=2 时，数值解为u1(x,t)=ΦT(x)U1Φ(x)，其中，U1如上所示.

故n=3时，该方程的数值解u2(x,t)=ΦT(x)U2Φ(x)，其中U2如上所示.

分别取t=1/4，t=3/4时，在部分取值点处，精确解和数值解的绝对误差见表1-2.

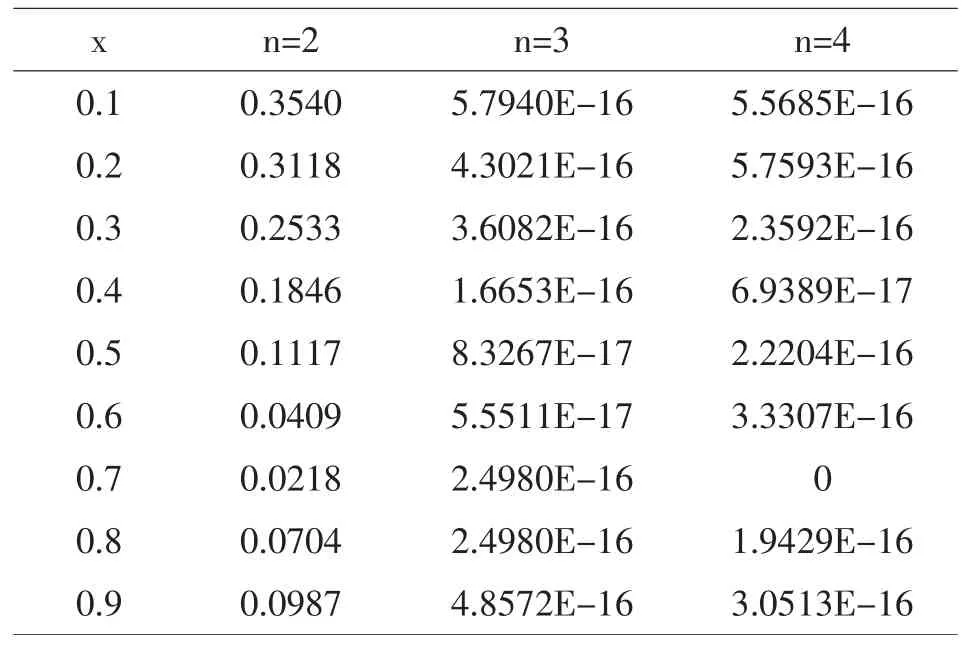
表1 t=1/4数值解与精确解的绝对误差

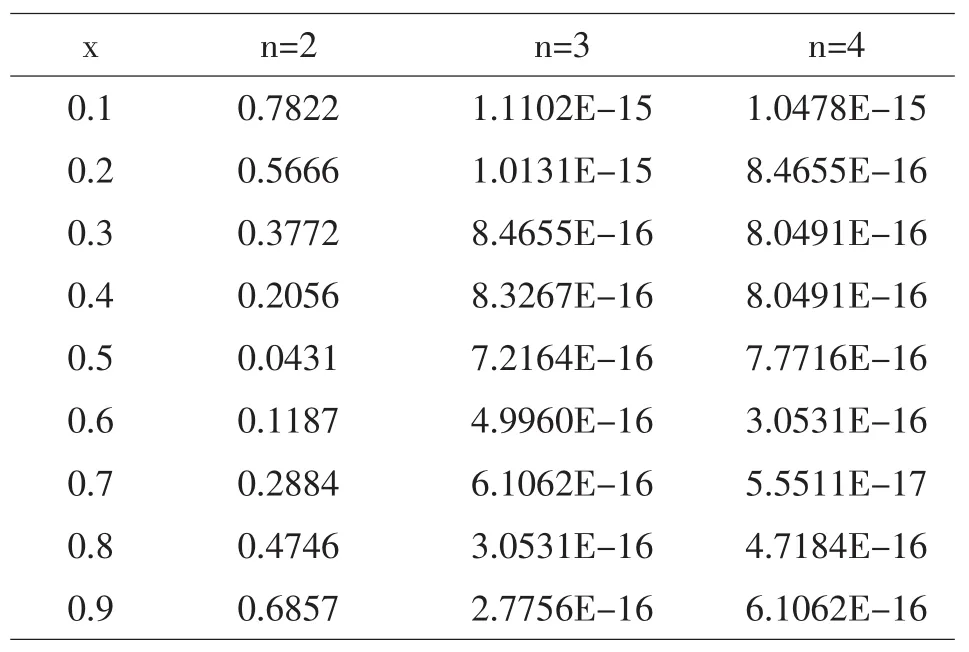
表2 t=3/4数值解与精确解的绝对误差

由上表可以观察到当取n=2时，数值解与精确解的误差大.而当n=3,4时，数值解与精确解的误差接近于10-15.表1-2表明，当合理设置截断项n,本文提出的方法是可行且有效.

3 结论

本文在Caputo类型的变分数阶微分定义下，根据变分数阶微分的性质，推导出了移位切比雪夫多项式的变分数算子矩阵，结合配点法，将求解变时间分数阶扩散方程问题转化为求解代数方程组，并结合算例说明了该方法可行性及有效性.本文的研究为进一步探讨变分数阶微分方程的数值计算方法奠定了一定的理论基础，具有一定的工程实用价值.另外，本文针对该方法的计算误差、收敛性分析等问题还存在欠缺，这也是笔者下一步努力的方向.