强度折减法在FLAC 3D数值模拟中的应用

章显斌 余以强

(1.福州职业技术学院，福建 福州 350108； 2.浙江省交通运输科学研究院，浙江 杭州 311305)

1 概述

许多土建工程中常会遇到土坡的稳定问题。如果处理不当，将会出现施工中的工程事故或影响工程的安全运营，所以有必要对土坡的稳定性作出评价。现在分析土坡稳定的方法主要有刚体极限平衡法、现代岩土数值分析方法。刚体极限平衡法将岩土体视为刚体，运用极限平衡理论进行边坡稳定性分析，没有考虑岩土体内部的应力应变关系，无法分析边坡破坏的发生和发展过程，无法考虑变形对边坡稳定的影响，无法考虑岩土体与支挡结构的共同作用及其变形协调[1]。而随着计算机技术的发展和数值计算技术的提高，FLAC强度折减法在边坡稳定分析的应用较好地解决了上述缺点。利用该法进行边坡稳定性分析时，可以考虑岩土体的非线性本构关系，求得边坡中某一点的应力、位移曲线，也可以对土体考虑大变形问题，这些都能比较真实的反映边坡的实际情况。

2 FLAC强度折减法

2.1 FLAC 3D简介

快速拉格朗日分析(Fast Lagrangian Analysis of Continua，简称FLAC)是近年发展起来的一种新型的数值分析方法，它首先由Cundall在1980年提出并将其程序化、实用化。FLAC与以往的差分分析方法相比，具有以下优点：

1)不但能处理一般的大变形问题，而且能模拟岩体沿某一薄弱面产生的滑动变形；

2)能针对不同的材料特性，使用相应的本构方程来比较真实地反映实际材料的动态行为；

3)可考虑锚杆、挡土墙等支挡结构与围岩的相互作用[2]。

建立FLAC 3D计算模型包含以下三个过程:1)有限差分网格生成;2)本构特性与材料参数设置;3)边界条件与初始条件设置。完成以上工作后，可以获得模型的初始平衡状态，然后改变边界条件来进行工程的响应分析，进行一系列计算步骤后得到问题的解。最后，进行结果的分析与总结[3]。

2.2 强度折减法原理

工程界广泛采用稳定安全系数(简称稳定系数)来评价边坡的稳定性。岩土坡沿着某一滑裂面的稳定系数F定义为：将岩土体的抗剪强度指标降低为c′/F，tanφ′/F，当沿着此滑裂面的岩土体处处达到极限平衡时对应的折减系数F即为稳定系数。在数值分析中，此类方法便成为强度折减法，其具体计算公式为：c′=c/F，φ′=arctan(tanφ/F)，基本原理为：不断降低c,φ值，直到破坏，破化时c,φ的降低倍数F就是稳定系数[2]。

2.3 模型中的屈服函数及塑性势函数

摩尔—库仑屈服准则：

τ=σntanφ+c。

其中，c,φ,σn分别为粘聚力、摩擦角、剪切面上的法向应力。转换成单元形式为：

塑性势函数为：

Q=σ1-σ3NΨ。

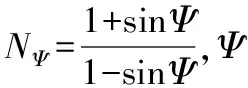
当φ=Ψ时为关联流动法则，当φ≠Ψ时为非流动法则。

3 边坡失稳破坏判据

在采用强度折减法进行边坡稳定分析时，目前存在的判断边坡失稳破坏的准则主要有[4-6]：

1)迭代求解的不收敛性准则，即当迭代计算到不收敛时认为边坡失稳破坏，此时的折减系数便为稳定系数。

2)塑性区的范围及其贯通状态准则，当边坡土体中的塑性区上下贯通时，便认为整个边坡产生滑动破坏了。

3)特征点位移准则，以某个特征点的位移为标准，计算时当强度折减到某一数值时该特征点的位移产生突变，边坡发生破坏。

4)广义剪应变或广义塑性应变贯通准则。本文采用迭代求解的不收敛性准则作为边坡失稳破坏的判据。

4 算例分析

算例边坡土质均匀，无孔隙水，土重18 kN/m3，坡高5 m，坡度1∶2，左右向两边无限延伸。边坡采用FLAC 3D 2.10版本进行数值模拟分析。边坡左右边界为水平约束，坡体底边界为固定约束，其计算模型和材料参数分别见图1，表1。

表1 材料参数

重度γ/kN·m-3体积模量/MPa剪变模量/MPa粘聚力c/kPa摩擦角ϕ/(°)18160361015

强度折减法计算时屈服准则采用摩尔—库仑准则，流动法则采用关联流动法则。计算结果见表2。

表2 计算结果及比较

由此可见，强度折减法求出的结果与刚体极限平衡法得出的结果很相近，说明强度折减法可以用于分析边坡的稳定性问题。而且该算例边坡的稳定性系数大于1.3，满足规范对边坡稳定安全系数的要求。

5 结语

通过上述算例的分析，可以得到：

1)强度折减法同刚体极限平衡法相比不仅能满足力的平衡方程而且也满足土体的应力和应变关系，最后求出的安全系数与刚体极限平衡法得出的结果很相近，说明强度折减法可以用于分析边坡的稳定性问题。

2)该算例边坡的稳定性系数大于1.3，满足规范对边坡稳定安全系数的要求。

强度折减法在岩土工程上虽然有一定的应用，但影响该方法计算精度的因素仍有很多，如边界范围、网格疏密、屈服准则的选取、不同流动法则的影响，弹性模量及泊松比的选取等，这些都将有待进一步的探讨和研究。