磨损面积扩散率对闸瓦磨损寿命的影响

罗 迎 ，杨兆建

（1.太原理工大学 机械工程学院，山西 太原 030024；2煤矿综采装备山西省重点实验室，山西 太原 030024）

1 引言

目前生产的各型号的矿井提升机制动一般都采用盘式制动系统与电控系统综合制定系统[1]，执行装置是灵活配置的闸瓦通过蝶簧产生的正压力压紧制动盘侧面，通过摩擦产生制动力或制动力矩，将提升系统的机械能转化为热能从而实现可靠制动[2]。盘式制动器闸瓦基体一般采用酚醛树脂基增强纤维树脂材料[3]，属于非金属聚合物闸瓦[4]，其机械性能要求较高[5]。制动盘的耐磨性高于闸瓦，因此分析闸瓦的磨损，是考察盘式制动系统的可靠性的重要内容[6-7]。

国内外文献对于磨损量的计算通常采用以下7个参数：

（1）WL线磨损—以单位时间摩擦表面法向尺寸减少计量的磨损；

（2）WV体积磨损—以单位时间体积减少计量的磨损；

（3）WM质量磨损—以单位时间质量减少计量的磨损；

（4）Wr磨损率—指磨损量对产生磨损的行程或时间之比，它可用三种方式表示，即单位滑动距离的材料磨损量；单位时间的材料磨损量；每转或每一往复行程的材料磨损量，

（5）相对磨损率：被试验材料磨损率与标准材料在相同条件下的磨损率之比；

（6）相对耐磨性δ及磨损系数ψ；

上述参数在磨损计算时往往对磨损的时变特征考虑的不够充分。文中通过磨损面积扩散率表述磨损的时变特征，针对矿用盘式制动器闸瓦磨损[8]扩散率与未磨损面积的关系，建立磨损面积微分方程，并探索方程解法，分析闸瓦寿命估计的简便计算方法。这些内容不仅可用于闸瓦的磨损计算和寿命估计，而且推导所用的分析方法和解法亦广泛适用于其它接触面磨损计算。

2 盘式闸瓦磨损过程分析

不考虑制动盘偏摆因素情况下，按时间历程分以下3个阶段：

（1）磨合阶段，轮廓接触发生在宏观几何形状相对较高的区域（主要是安装误差引起的端面不平度），蝶簧力作用在局部区域，根据库伦定律，制动力并未减小，但较高的局部正压力促使磨损加剧，磨损面积增大，局部正压力减小，磨损率降低，表面形貌的几何尺度进入表面波纹度（值的大小主要受加工方法所限）的数量级。从表面形貌的几何尺度进入表面波纹度的数量级直至微观几何数量级阶段是稳定磨损[9]，只是后者相对前者接触面积进一步增大；

（2）稳定磨损阶段。磨损面积近似等于名义接触面积；

（3）闸瓦的磨损使闸瓦报废更换阶段，此时因闸瓦的磨损使制动力矩不能满足要求，或者，或者调整闸瓦间隙后虽然制动力矩满足要求，但闸瓦的机械性能已不满足要求。

3 基于磨损面积扩散率的闸瓦磨损模型的建立

A1，A2，…AN表示 t1，t2，…tN时刻摩擦副实际接触面积，如图1所示。是由众多的离散的小接触面积的统计和值，分析如下：在闸瓦磨损过程中，由于在接触区闸瓦材料的弹塑性变形，实际上，磨损面积略大于实际接触面积，理论上一般认为闸瓦的磨损面积近似等于实际接触面积。

图1 基于磨损面积扩散率的闸瓦磨损模型示意图Fig.1 The Model of Brake Shoe Wear Based on Wear Area Diffusion Rate

闸瓦-制动盘摩擦副名义接触面积S=a×b是一定值。而对于单位时间内磨损面积的与原磨损面积[10]的关系，从逻辑上需要分磨合阶段、稳定磨损阶段。在稳定磨损阶段，闸瓦-制动盘摩擦副的磨损面积等于名义接触面积，因此单位时间内磨损面积的增量在外载荷、环境介质因素不变的情况下是与名义接触面积呈某一比值，这一比值即为磨损面积扩散率，设此定值为k0；在磨合阶段，磨损面积扩散率视作变量，以符号k表示，因此，当外载荷、环境介质因素不变的情况下可近似认为磨损面积的增量与前一时刻的磨损面积呈比值 k 的关系，即 A（t+Δt）-A（t）=kA（t），将闸瓦磨损视作连续的过程，磨损面积扩散率通过时刻t时未磨损面积B（t）给出定义式，这是符合实际磨损过程的，事实上磨损面积扩散率与已磨损面积A（t）并无直接关系，反而在其它工况因素已定的情况下由未磨损面积决定：k=μB（t） （1）

式中：μ—制动过程中未磨损面积向磨损面积的瞬时转化速率，作为变量符号引入，近似计算中，其值与时间存在联系，但没有时间累积性，故在积分过程中可视作常量；如果将μ视作时间变量，则进入二元微分方程组的求解，而二元微分方程这求解出因变量的具体表达式局限性很强。

μ的影响因素包括制动工况、材料、环境介质等。制动工况参数包括相对滑动速度、外载荷、制动盘偏摆值、闸瓦及制动盘安装误差等；材料参数主要指材料的表面几何参数、表面性质参数（主要指强度、硬度、热稳定性、抗疲劳等）；环境介质参数主要包括吸附膜、温升等；冲击与振动也影响了μ的取值。这些因素强耦合在一起，参数间数量级特别是每一因素的影响权重在不同的制动工况、制动方式下取值不同，这也是没有从这些参数中选取自变量，而是从磨损面积扩散率着手建立微分方程以近似估计闸瓦寿命、磨合时间、闸瓦定期更换的周期的原因；

设摩擦副在其寿命周期内某一时刻的磨损面积为A（t）、未磨损面积B（t），名义接触面积S，则：

S=A（t）+B（t）

A（0）=A0

式中：A0—制动甫始接触面积；A（t+Δt）-A（t）=μB（t）·A（t）·Δt微分化；

4 闸瓦磨损模型的求解

对于（2）式采用两种方法求解：

4.1 直接解法

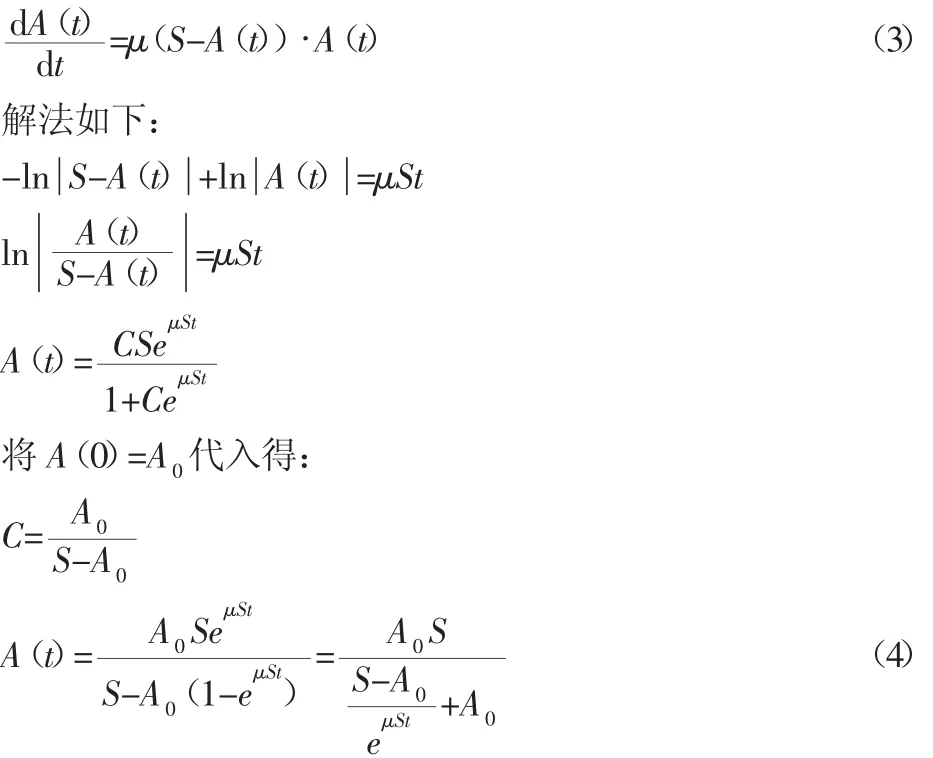
4.2 伯努利（Bernoulli）方程解法

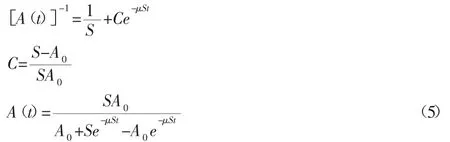
求算结果式（4）与式（5）相同，验证了解法的正确性，也反应了磨损面积模型的有效性。在此佐以举例：制动盘直径D=200mm，扩散速度k=0.01mm2/h，时间度量以小时h为单位，单位时间后的磨损面积：A（1）-A（0）＝kA（t）·Δt=0.01·A（0）·1，可得 A（1）=1.01A（0）＝1.01A0，同时≈1.01A0，可见在这一假设条件下，在磨合过程开始阶段磨损面积与闸瓦的名义接触面积S关系并不大，主要取决于初始磨损面积。

对式（5）求导以考察其性质，易知 A（t）′＞0：

图2 磨损面积变化曲线Fig.2 The A（t） Curve with the Time

图3 磨损面积扩散率变化曲线Fig.3 The dA（t）/dt Curve with the Time

图4 磨损面积变化率的增幅随时间的变化曲线Fig.4 The A（t）′′ Curve with the Time

易得A（t）′′的表达式如下，并绘出曲线，曲线清晰的表明了磨损率在某个区域变化幅度很大，而其它时间段，磨损率较为稳定：

求解结果的分析：

（1）式（6）表征了磨损面积与时间之间的关系，由图2即式（6）曲线性质可知，随制动时数的增加，磨损面积逐渐增大，开始阶段磨损面积的增率较小，原因是此时其增量受闸瓦安装误差引起的端面不平度影响；中间阶段接近线性增长，原因在于此时其增量受制造加工时产生的表面波纹度影响；当接近0.95s的时候，增速变缓，主要原因在于此时受表面形貌的微观表面不平度影响；之后的磨合终了阶段，轮廓接触面积近似等于名义接触面积。

（2）从图3即式（7）曲线性质可分析出，随着磨损时间的增加，磨损面积扩散率逐渐增大，当达到峰值后逐渐减小至接近于零，达到峰值的时间 t峰可以令 A（t）′′=0 求出，经计算 t峰的表达式如下：

（3）又由图2可知，当t→∞时，A（∞）=S表明经磨合后最终等于名义接触面积S，而实际上是经过一定时长的磨合，接触表面进入稳定磨损阶段，这表明在磨合终了阶段，闸瓦磨损面积扩散率有很大幅度的降低，即这一阶段磨损面积值变化并不大，且其数值的变化对磨损参数影响不大，这一分析结果很好的诠释了JB/T 3721-1999矿用提升机盘形制动器闸瓦标准的“矿井提升所用闸瓦当接触面积达到配置的多副闸瓦之和的95%就认为进入稳定磨损阶段”的规定。

（4）由图4可得，开始制动阶段，在压力加载的过程中，闸瓦发生弹塑性变形，接触面积与压力P的指数值成比例，即满足A0，其中C为比例系数，由闸瓦材料决定，因矿用闸瓦一般是增强纤维型树脂基复合材料，故C值及具体的指数值必须由实验测定，由于（0～A0）时间极短，故制动初期磨损面积约等于A0，所以在图4的磨损面积扩散率曲线上初期几乎为0；在磨合阶段，磨损面积扩散率的绝对值有较大增长；当有磨合阶段进入稳定磨损的过程中，磨损面积扩散率由最大值回复到接近零的状态，这与闸瓦的实际磨合过程是相符的。

（5）当闸瓦进入稳定磨损阶段，磨损面积略低于名义接触面积，当外载荷与工况条件相差不大的情况下，闸瓦的磨损厚度与时间成正比，即满足：

式中：h稳—稳定阶段磨损厚度；t稳—闸瓦在稳定阶段工作时长；λ—单位时间的磨损厚度，当外载荷与工况条件相差不大时一般取做定值。

（6）闸瓦磨损厚度计算。磨合阶段的磨损厚度是宏观几何误差、表面波纹度、表面粗糙度之和，一般可经验取值，因为这一数值在去除宏观几何误差的情况下与稳定阶段的磨损厚度相比较小，故在磨损厚度近似计算中不计入在精度上是可以接受的，同理当计算磨合阶段所用时间，可以令 A（t）=95%·S，JB/T3721-1999标准推荐规定“在低载低速工况下不低于72h”，所以此处不具体计算其值，直接以72h代入；JB/T 3721-1999规定“JK型提升机闸瓦与制动盘的间隙为（1～1.5）mm。如闸瓦磨损厚度超过2mm时应及时更换”，故有下式成立：

式中：t寿—闸瓦的使用寿命，单位小时 h；例如，矿用（280×200×30）规格闸瓦，稳定磨损厚度 2mm，另设 λ=10μm/h，λ 是多副闸瓦作用下单片闸瓦的磨损厚度，计算的闸瓦工作时长为t寿=272h，据此值并结合闸瓦的使用频繁程度可有效确定闸瓦的更换周期。之所以出现磨合阶段时长72h与工作时长200h接近的原因是磨合阶段与闸瓦工作阶段相比外载荷与相对滑动速度都较低。

5 结论

经分析和例证表明：

（1）通过磨损面积扩散率对闸瓦磨损寿命估计所用的思路是明确的，建立的模型虽稍显繁琐，但模型与磨损深度、质量磨损率及体积磨损率等概念相比，更加符合实际磨损过程，伯努利方程解法对模型的适用性也很好。这些方式方法对计算其它接触表面的磨损具有普遍适用意义；

（2）通过基于闸瓦的磨损面积的时变性，得出闸瓦磨损寿命的近似式，从而可对闸瓦寿命做较为精确的近似计算。不足之处是缺乏足够的工业统计数据拟合出μ、λ随工况参数的变化曲线或以工况参数为自变量的高次多项式，影响了求解的精度。