多普勒非对称空间外差干涉仪调制度分析

施海亮 李志伟 罗海燕 熊伟



多普勒非对称空间外差干涉仪调制度分析

施海亮 李志伟 罗海燕 熊伟

（中国科学院安徽光学精密机械研究所，中国科学院通用光学定标与表征技术重点实验室，合肥 230031）

多普勒非对称空间外差光谱仪是近年得以迅速发展的新型中高层大气风场探测仪器，具有视场展宽、大光通量、高光谱分辨和多谱线同时探测等特点。该仪器的干涉调制度是影响风场反演精度的关键指标。文章基于非对称空间外差光谱技术基本原理，推导了干涉仪视场展宽前后的干涉理论积分公式，分析了干涉调制度与仪器视场角、最优光程差的关系，通过对干涉方程中像元采样积分推导得到干涉调制度与采样间隔的理论形式，仿真了干涉调制度与仪器视场角、最优光程差和采样间隔的定量关系曲线，并通过实验室搭建试验装置对分析结果进行验证。研究结果表明：随着非对称空间外差干涉仪视场角和光程差偏置量的增加，干涉调制度降低；调制度沿着波数增大的方向上升，在同一波数处，随着采样间隔的增加，干涉调制度降低。理论分析和试验测量结果调制度最大偏差0.02，分析与实测结果一致性较好。

多普勒外差干涉仪 调制度 视场角 最优光程差 相位频移 空间大气探测

0 引言

中高层大气对于研究全球气候变化、大气物理模型和航空航天活动具有重要的指导意义[1-4]，其中风场信息表征了大气动态变化，是获取大气行为的关键因子。多普勒非对称空间外差光谱技术（Doppler Asymmetric Spatial Heterodyne Spectroscopy，DASHS）作为新兴的被动式风场探测手段成为近些年的研究热点。该技术2006年由J. M. Harlander等人提出，基于对称空间外差光谱技术（Spatial Heterodyne Spectroscopy，SHS）[5]而改进，综合空间干涉与光栅衍射于一体，不仅继承了传统迈克尔逊干涉光谱仪的优点，避免了运动部件和窄带滤波，而且能够同时测量多个谱线，具备系统误差同步探测的特点，具有较高的风场探测精度以及较强的空间环境适应性[6]。

采用非对称空间外差技术进行风场测量是依据多普勒以及傅里叶变换原理，通过对干涉图进行傅里叶变换获取气辉目标光谱，然后逆变换获取复数形式的干涉图，由干涉图的实虚部比求出光程差范围内每个点的相位，最终通过相位信息的变化量反演得到风速[7-9]。干涉调制度是非对称空间外差干涉仪进行风场探测过程中需要考虑的一个关键因素。调制度的大小直接影响了干涉条纹的品质，进而经过目标光谱获取和相位频移信号提取后，导致风速反演精度降低。影响调制度的因素是多方面的，具体包括干涉仪的视场角、最优光程差和采样间隔等。其中，由于扩视场前后的非对称空间外差干涉方程的差异，调制度与视场角的关系也并不相同。

基于以上考虑，本文从非对称空间外差技术的基本原理出发，分析并推导了与视场角和采样间隔相关的积分干涉方程，得到干涉调制度公式；定量分析了仪器视场角、光程差偏置量和采样间隔等系统参数对干涉调制度的影响；进而用于指导多普勒非对称空间外差干涉仪风场探测仪器的方案设计和工程实现。

1 非对称空间外差光谱技术原理

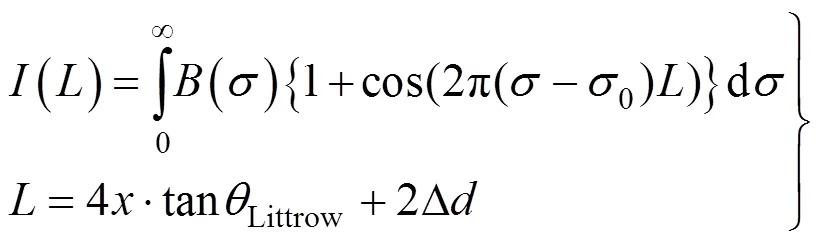
由于风速引起的多普勒频移量非常小，传统光谱仪或干涉仪难以探测到如此微小的光谱频移。在传统的空间外差干涉仪的一臂上通过增加光程差偏置，可以增大由风速引起的干涉相位变化量，探测此相位变化可反演获得风速。然而，考虑到干涉调制度会随光程差的增加而减小，因此多普勒外差干涉仪存在一个最优光程差opt[6-7]

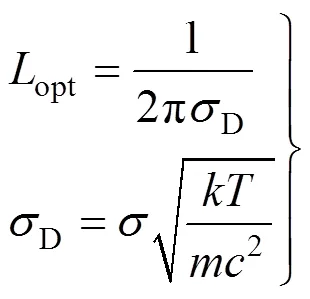
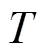
单色光照明理想条件下，干涉图调制度为1，调制度定义为

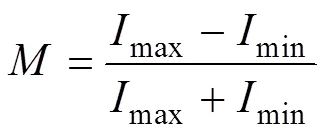
式中max为干涉条纹最大值；min为干涉条纹最小值。

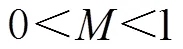
2 仪器视场角与干涉调制度

为了获得一定的输入辐射强度，实际均采用有特定尺寸的扩展光源，对仪器有一定的立体角。对于某一单色光p，扩展光源将引起谱线展宽，使干涉条纹对比度降低，降低分辨率。为了满足仪器的探测需求，干涉图要有较高的调制度，DASHS干涉方程可以直接由空间外差干涉方程推导得到[11-14]，这是因为干涉方程是对立体角积分，而与光程差无关。在非扩视场的情况下，当立体角为时，干涉条纹强度可以写成如下形式

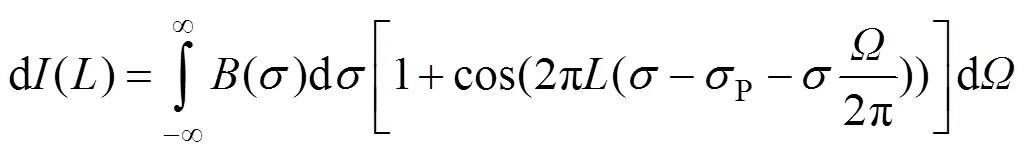
对方程（4）的立体角从0到s进行积分得

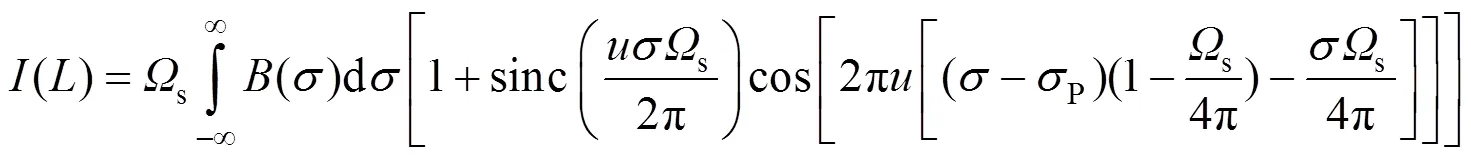
式中为光栅有效截面长度。

式（5）积分号前面的s代表由于有限视场角而引起的条纹强度的增加值，非扩视场的干涉调制函数可以写为

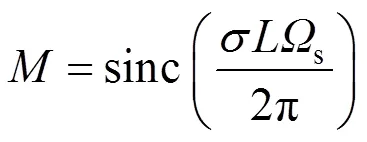
在实际应用中，为了增加信噪比，在非对称空间外差干涉仪中通过扩视场技术增大仪器视场。扩视场后，上述干涉方程不再适用，根据光栅方程和扩视场棱镜出射光角度计算推导出空间外差干涉仪的扩视场方程[15-17]，进而得到非对称空间外差干涉仪的扩视场方程

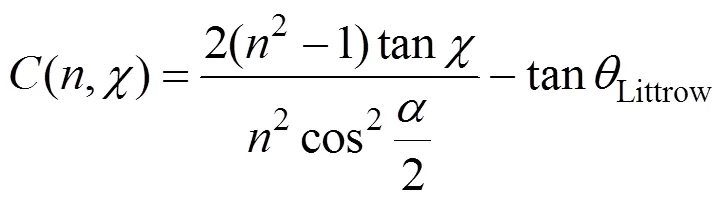
式中表示扩视场棱镜的折射率；表示光束经过扩视场棱镜后的出射角度；表示扩视场棱镜的顶角。

对立体角从0到s进行积分，根据方程（7）可得出

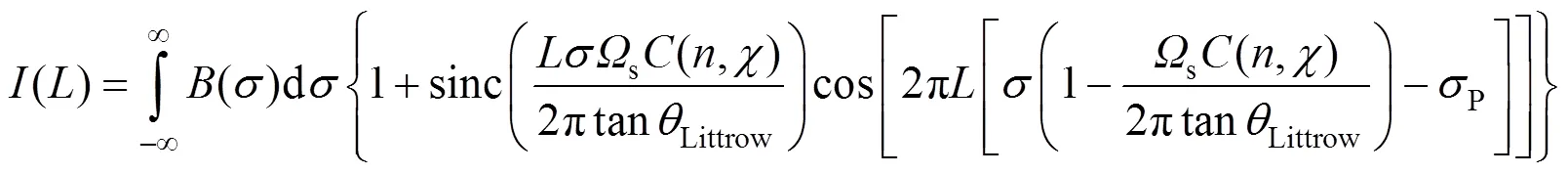
则扩展视场DASHS干涉仪的调制度函数为

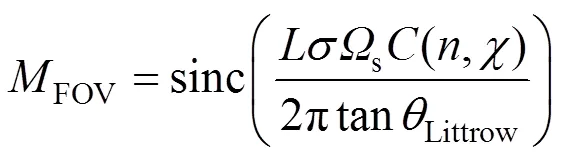
根据极限视场角的定义[5]，可计算DASHS干涉仪的极限视场半角。

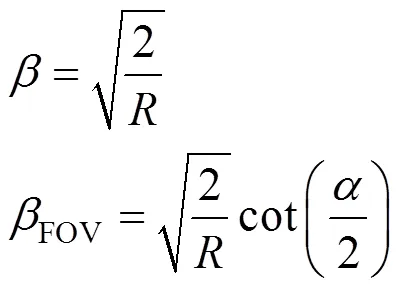
表1 DASHS干涉仪视场角参数

Tab.1 Angle of field of viewof the DASHS interferometer

根据表1计算的极限视场半角，在DASHS干涉仪扩展视场前，视场角小于极限视场半角时的调制度曲线，如图2所示。随着视场半角的增加，干涉调制度逐渐降低，当到达极限视场角0.14°时，干涉调制度约0.64。扩展视场后，极限视场增大，可以看出，视场角为0.91°时，理论上的干涉调制度才降至0.64，而在0.14°的地方，干涉调制度为0.999 79。分析结果表明，干涉仪扩展视场后，调制度得到了极大的改善。

3 光程差偏置量与干涉调制度

根据调制度方程，干涉调制度不仅是视场角的函数，也是光程差偏置量的函数。下面将对不同光程差偏置量off下的调制度（干涉仪扩视场条件下）对比，如图3所示。

由图3可知，对于扩展视场的DASHS干涉仪，其干涉调制度不仅随着视场半角的增加而减小，而且随着光程差偏置量off的增加而减小，因此必须选择合适的光程差才能保证满足调制度的需要。

4 数据采样间隔与干涉调制度

方程（1）给出的干涉图方程是在满足采样定理的条件下，将探测器上每个像元尺寸近似为无限小的条件下成立。事实上，探测器的像元实际都具有一定的尺寸，从而在一定程度影响了干涉调制度[18-20]。设探测器上单像元的尺寸为，在光谱维两个相邻的像元坐标记为1，2，1像元中心点到2像元中心点之间某一位置的长度为m，则有

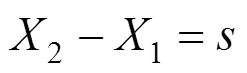
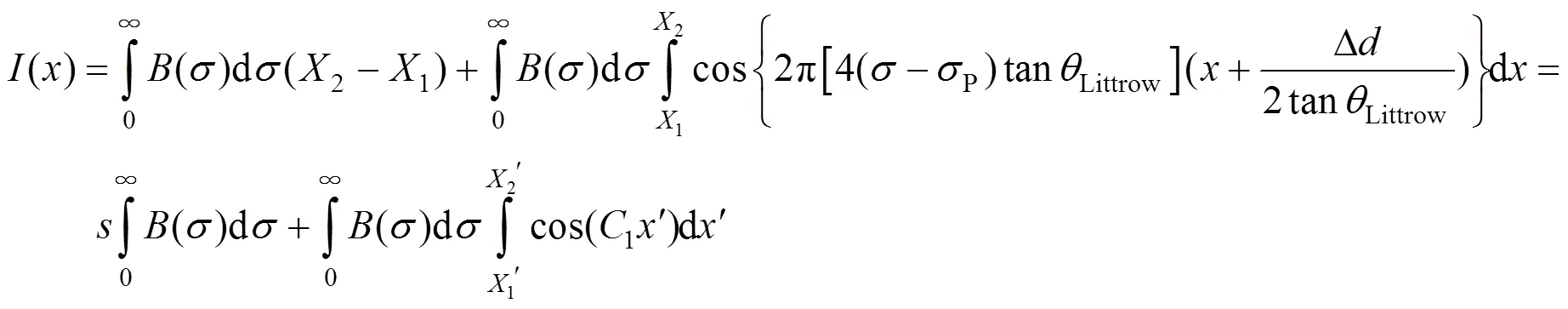
对积分项展开并计算可得

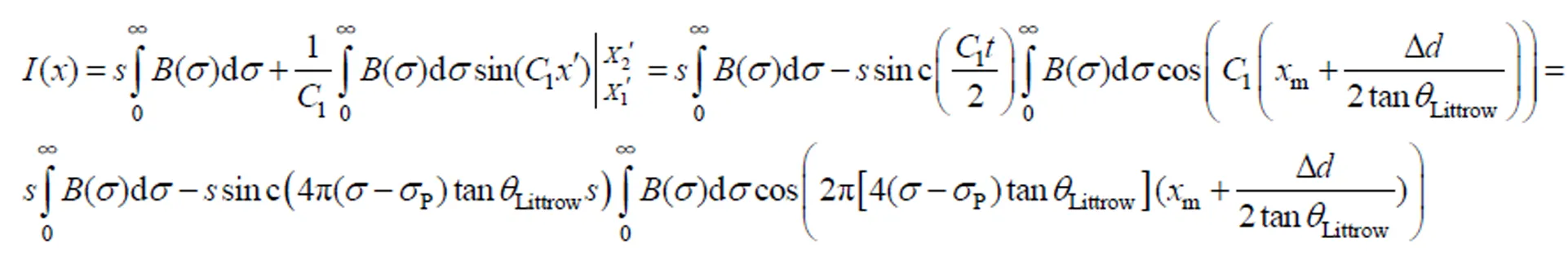
式中为探测器半尺寸。

因此，与像元尺寸有关的DASHS干涉仪调制度可以写为

已知CCD探测器像元尺寸为13 μm，Littrow波长为764.78 nm，Littrow角为13.2638°，带入得到调制度M与波数的关系曲线，见图4。

由图4看出，调制度沿着波数增大的方向上升，即在长波方向干涉调制度较低，在短波方向干涉调制度相对较高。另外，在同一波长处，随着像元尺寸的增加，干涉调制度降低，图中所给的像元尺寸最大为15μm。因此，满足采样定理前提下，为了减小探测器像元尺寸对调制度的影响，像元尺寸越小越好。

通过以上分析可知，影响DASHS干涉仪干涉调制度的因素是多方面的。由于干涉仪具有一定的视场角，因此通过对干涉方程中的立体角积分，可以得出干涉调制度随着视场角和光程差的增加而降低；通过对干涉方程中的探测器面上像元积分，可以得出干涉调制度随着像元尺寸的增加而降低，并且在短波方向干涉调制度较高。

5 试验结果与分析

中科院安徽光机所已成功搭建了基于DASHS原理的风场探测试验装置，针对760nm氧气气辉谱线进行风速探测[10]，根据仪器视场角和干涉调制度的分析结果，为了保证其中干涉仪采用扩视场一体化胶合设计，其中偏置光栅未进行最后胶合，通过移动光栅位置采集不同偏置量下的干涉数据。试验装置主要器件参数及系统的主要性能参数如表2所示。

试验采用钾元素空心阴极灯作为光源，在波段内具有两条波长分别为766.49nm和769.90nm的特征发射线。光源发出的光经过准直镜头后进入干涉仪，形成Fizeau条纹。在干涉仪出射端，干涉条纹被成像镜头按照1.6∶1的缩放比进行缩放，最终成像于CCD探测器面，移动偏置臂光栅距离分别为10、30、50、60、70mm，测量实测不同偏置量下的干涉图，如图5所示。

对原始干涉图扣除暗电流、去除探测器非均匀性校正和非线性校正影响、并且进行干涉图像相位校正后，计算干涉条纹的调制度，获得不同偏置量下实际干涉数据调制度，与相同偏置量下理论干涉图调制度对比，结果如表3所示。根据上文分析，获取视场半角0.6°对应不同偏置量的调制度因子、探测器像元13μm对应的调制度曲线均值及成像镜头MTF，计算不同偏置量理论干涉图调制度。

表2 多普勒非对称空间外差光谱仪主要器件参数

Tab.2 The main parameters of DASHS breadboard

表3 不同光栅偏置量调制度理论与实测调制度

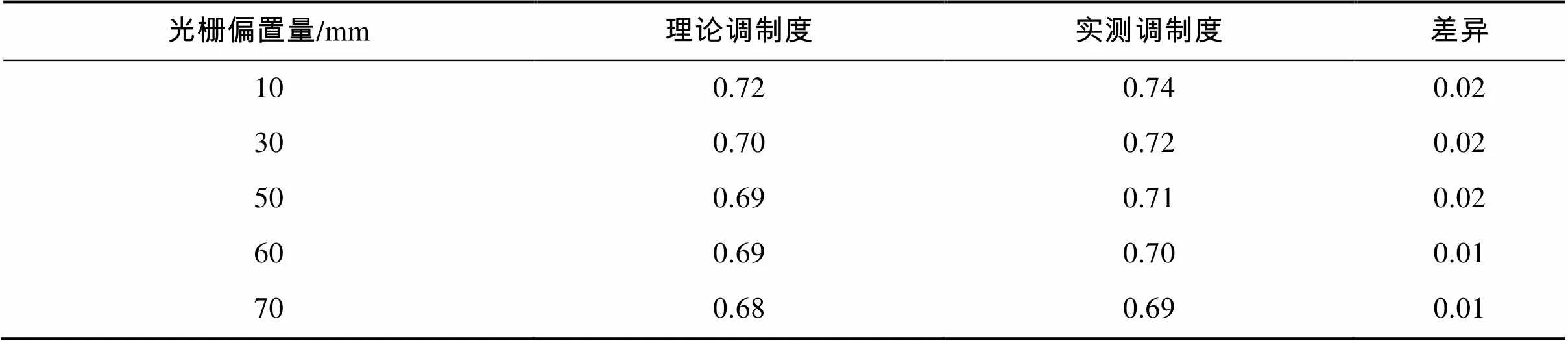
Tab.3 The theoretical modulation efficiency and the measured with different grating offsets

由表3对比分析可知，理论获得的干涉图调制度与实测干涉图调制度一致性较好。需要指出的是，表3中理论调制度计算时探测器像元大小和成像镜头MTF的影响，均是以滤光片在整个波段内的均值，理论调制度与实测干涉图调制度的微小偏差是由于探测器的噪声、计算模型的简化、成像镜头的MTF误差等因素造成。

6 结论

本文在空间外差干涉方程的基础上推导了扩视场前后的非对称空间外差干涉方程，得出干涉调制度与仪器视场角和最优光程差的定量关系，并对有限尺寸的探测器像元推导了像元尺寸与调制度的关系，首次从理论上分析了多普勒非对称空间外差干涉仪调制度的影响因素，在实验室搭建试验装置采集不同光栅偏置量下的干涉数据，对实测干涉图调制度和理论调制度进行了对比分析，得到以下结论：

1）随着视场角的增加，干涉调制度降低；

2）对比扩展视场前后的调制度曲线得出，视场展宽有效提高了干涉调制度；

3）对比同一视场下的干涉调制度得出，随着光程差偏置量的增加，干涉调制度降低；

4）随着像元尺寸的增加，调制度降低，且调制度沿着波数增大的方向上升。

通过定量分析仪器视场角、光程差偏置量与探测器像元尺寸对多普勒空间外差干涉仪调制度的影响，可保证多普勒非对称空间外差干涉通过优选参数提升调制度，获取更有效的干涉频移信号。该结论可为仪器系统设计参数选择提供重要理论依据，对仪器方案优化及工程研制具有重要的指导意义。

[1] SHEPHERD G G, THUILLIER G, GAULT W A, et al. WINDII, the Wind Imaging Interferometer on the Upper Atmosphere Research Satellite[J]. Journal of Geophysical Research: Atmospheres (1984-2012), 1993, 98(D6): 10725-10750.

[2] HAYS P B, ABREU V J, DOBBS M E, et al. The High-resolution Doppler Imager on the Upper Atmosphere Research Satellite[J]. Journal of Geophysical Research, 1993, 98(D6): 10713-10723.

[3] KILLEEN T L, SKINNER W R, JOHNSON R M, et al. TIMED Doppler Interferometer (TIDI)[J]. Optical Spectroscopic Techniques and Instrumentation for Atmospheric and Space Research III, 1999, 3756: 289-301.

[4] MCLANDRESS C, SHEPHERD G G, SOLHEIM B H, et al. Combined Mesosphere/ Thermosphere Winds Using WINDII and HRDI Data from the Upper Atmosphere Research Satellite[J]. Journal of Geophysical Research, 1996, 101: 10441-10453.

[5] HARLANDER J M. Spatial Heterodyne Spectroscopy: Interferometric Performance at Any Wavelength Without Scanning[D]. Wisconain, USA: The University of Wisconain, 1991.

[6] ENGLERT C R, HARLANDER J M, BABCOCK D D, et al. Doppler Asymmetric Spatial Heterodyne Spectroscopy (DASH: An Innovative Concept for Measuring Winds in Planetary Atmospheres[J]. SPIE Atmospheric Optical Modeling, Measurement, and Simulation II Optics+ Photonics, 2006, 6303: 290-296.

[7] ENGLERT C R, BABCOCK D D, HARLANDER J M. Doppler Asymmetric Spatial Heterodyne Spectroscopy (DASH): Concept and Experimental Demonstration[J]. Applied optics, 2007, 46(29): 7297-7307.

[8] ENGLERT C R, HARLANDER J M, EMMERT J T, et al. Initial Ground-based Thermospheric Wind Measurements Using Doppler Asymmetric Spatial Heterodyne Spectroscopy (DASH)[J]. Optics Express, 2010, 18(26): 27416-27430.

[9] HARLANDER J M, ENGLERT C R, BABCOCK D D, et al. Design and Laboratory Tests of a Doppler Asymmetric Spatial Heterodyne (DASH) Interferometer for Upper Atmospheric Wind and Temperature Observations[J]. Optics Express, 2010, 18(25): 26430-26440.

[10] 沈静, 熊伟, 施海亮, 等. 用于风场探测的多普勒非对称空间外差干涉数据处理方法研究[J]. 光谱学与光谱分析, 2016, 36(9): 3014-3019. SHEN Jing, XIONG Wei, SHI Hailiang, et al. Doppler Asymmetric Spatial Heterodyne Interference Data Processing Methods Used in Wind Field Detection Research[J]. Spectroscopy and Spectral Analysis, 2016, 36 (9): 3014-3019. (in Chinese)

[11] 沈静. 中高层大气风场探测多普勒非对称空间外差技术研究[D]. 合肥: 中国科学技术大学, 2016. SHEN Jing. Doppler's Asymmetric Spatial Heterodyne Technology for Mid and Upper Level Wind Field Detection[D]. Hefei: University of Science & Technology China, 2016. (in Chinese)

[12] SHEN J, XIONG W, SHI H L. et al. Data Processing Error Analysis Based on Doppler Asymmetric Spatial Heterodyne (DASH) measurement[J]. Applied Optics, 2017, 56 (12): 3531-3537.

[13] 李志伟, 熊伟, 施海亮, 等. 非对称空间外差光谱技术研究[J]. 光谱学与光谱分析, 2016, 36(7): 2291-2295. LI Zhiwei, XIONG Wei, SHI Hailiang, et al. Research on Asymmetric Spatial Heterodyne Spectroscopy[J]. Spectroscopy and Spectral Analysis, 2016, 36(7): 2291-2295. (in Chinese)

[14] SHEN Jing, XIONG Wei, SHI Hailiang, et al. Phase Detection and Drift Correction for Doppler Asymmetric Spatial Heterodyne Interferometer[J]. Acta Photomica Sinica, 2017, 46(9): 114-120.

[15] 叶松. 空间外差光谱技术研究[D]. 北京: 中国科学院研究生院, 2006. YE Song. Spatial Heterodyne Spectroscopy Technology[D]. Beijing: Graduate University of Chinese Academy of Sciences, 2006. (in Chinese)

[16] 施海亮.空间外差光谱仪定标技术研究[D]. 北京: 中国科学院研究生院, 2012. SHI Hailiang. Spatial Heterodyne Spectrometer Calibration Technology[D]. Beijing: Graduate University of Chinese Academy of Sciences, 2012. (in Chinese)

[17] 罗海燕. 空间外差干涉成像光谱技术研究[D]. 北京: 中国科学院大学, 2015. LUO Haiyan. Spatial Heterodyne Interferometric Imaging Spectroscopy Technology[D]. Beijing: University of Chinese Academy of Sciences, 2015. (in Chinese)

[18] 陶然, 相里斌, 杜述松, 等. 高通量傅里叶变换成像光谱仪调制度分析[J]. 光子学报, 2006, 35(5): 675-679. TAO Ran, XIANG Libin, DU Shusong, et al. High Throughput Fourier Transform Imaging Spectrometer Modulation Analysis[J]. Acta Photorica Sinica, 2006, 35(5): 675-679. (in Chinese)

[19] 杨建峰, 相里斌, 高瞻, 等. 干涉成象光谱仪中前置光学系统远心角对干涉调制度的影响[J]. 光子学报, 1997, 26(4): 368-372. YANG Jianfeng, XIANG Libin, GAO Zhan, et al. Influence of the Far Optical Angle of the Front Optical System on Interferometric Modulation in Interferometric Imaging Spectrometer[J]. Acta Photorica Sinica, 1997, 26(4): 368-372. (in Chinese)

[20] 张淳民, 相里斌, 杨建峰, 等. 稳态大视场偏振干涉成像光谱仪原理及调制度分析[J]. 西安交通大学学报, 2000(6): 93-97. ZHANG Chunmin, XIANG Libin, YANG Jianfeng, et al. The Principle and Modulation Analysis of the Steady-state Large Field Polarization Interference Imaging Spectrometer[J]. Journal of Xi'an Jiaotong University, 2000(6): 93-97. (in Chinese)

The Modulation Efficiency Analysis of Doppler Asymmetric Spatial Heterodyne Spectrometer

SHI Hailiang LI Zhiwei LUO Haiyan XIONG Wei

（Anhui Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Key Laboratory of Optical Calibration and Characterization, Hefei 230031, China）

As a new type of the detection instrument for upper atmospheric wind field, Doppler asymmetric spatial heterodyne spectrometer has been rapidly developed in recent years, with many simultaneous characteristics such as broadening view, large flux, high spectral resolution and multispectral detection ability. The interference modulation efficiency is the key parameter affecting the wind field retrieval precision. Based on the basic principle of asymmetric spatial heterodyne spectroscopy, the integral formula in the interference theory is derived before and after enlarging the view, and the relationship among the interference modulation efficiency, angle of field of view and the optimal optical path difference is analyzed. The theoretical expressions of the interference modulation efficiency and the sampling interval are derived by the pixel sampling integration in the interference equation, and the quantitative relationship curve among the interference modulation efficiency, the angle of field of view and the optimal optical path difference is simulated, and then validated by the laboratory breadboard. The results show that the interference modulation efficiency decreases while increasing the viewing angle and the offset of the optical path difference, and increases with the rise of the wave number or adding the sampling interval at same wave number. The derived modulation has good agreement with the theoretical calculation results, with the maximum error less than 0.02.

Doppler heterodyne interferometer; modulation efficiency; field of view; optimal path difference; phase shift; space atmosphere detection

O433.4

A

1009-8518(2018)05-0057-09

10.3969/j.issn.1009-8518.2018.05.008

施海亮，男，1983年生，2012年获中国科学院研究生院光学专业博士学位，副研究员。研究方向为高光谱遥感探测技术。E-mail：hlshi@aiofm.ac.cn。

2018-03-12

遥感科学国家重点实验室开放基金（Y7Y00100KZ）；国家自然科学基金（41301373）

（编辑：王丽霞）