基于滑移网格技术的翼伞动导数分析

王世超 贺卫亮



基于滑移网格技术的翼伞动导数分析

王世超 贺卫亮

（北京航空航天大学 宇航学院，北京 100191）

翼伞在航天回收领域有着广泛的应用前景，为了提高对翼伞动稳定性认识，文章针对某型号的翼伞进行动导数的分析。基于滑移网格技术，采用计算流体学的方法对翼伞进行了三维数值模拟。重点分析了翼伞做小幅度俯仰、偏航和滚转运动时的动导数，通过改变攻角和减缩频率这两项重要参数，获取了多组力矩系数迟滞曲线，利用时间平均法对非定常气动力数据进行处理，得到了翼伞绕三个坐标轴的阻尼系数。计算结果表明：翼伞在小攻角下做小幅度强迫运动时，在俯仰和滚转方向上阻尼导数为负，翼伞具有俯仰和偏航方向上的动稳定性，在偏航方向阻尼导数为正，翼伞不具有偏航方向的动稳定性；攻角和减缩频率的选取均会影响翼伞阻尼导数的计算结果，其中，攻角的增加不仅能影响迟滞环面积的大小还能影响迟滞环的动态特性，使翼伞的动稳定性发生变化，而减缩频率的改变仅影响迟滞环面积的大小，对偏航方向的动稳定性没有影响。

滑移网格 攻角 减缩频率 动导数 翼伞 航天回收

0 引言

与常规圆形降落伞不同，翼伞充气后，形状接近机翼，具有与机翼相似的气动特性，拥有较好的滑翔性能，并且通过控制翼伞后缘的操纵绳，可以改变翼伞的气动外形，从而有效地操纵翼伞制动或转弯。鉴于翼伞良好的可操纵性，世界上许多国家利用翼伞进行物资精确投送。为了提高对翼伞的气动性能认识，完善翼伞控制系统设计，有必要对翼伞的动导数进行分析和计算。

动导数[1]指的是单位速度或角速度变化引起的气动力或力矩的变化，以导数形式表达。这些参数是飞行器的稳定性分析和控制系统设计中不可或缺的气动参数。对于动导数的确定，现有的方法有风洞试验、飞行试验和理论分析计算。飞行试验和风洞试验成本高、周期长，难以满足工程人员的需要。理论分析计算主要包括工程估算和数值模拟，早期研究动导数主要是经验和半经验公式为代表的工程估算方法，包括牛顿理论、活塞理论、升力线理论和升力面理论等[2-3]。但是这些理论方法精度不高，只适合外形比较简单的结构，难以满足现有飞行器设计的需要。国内外学者采用计算流体力学的方法来模拟求解飞行器的动态稳定性参数，并取得了较大的成果，在一定的程度上能够满足工程应用的需要。文献[4]采用双时间步法对Finner导弹进行了动导数的数值模拟；文献[5]采用非线性减缩频率方法模拟单一频率的强迫振动求解动导数；文献[6-8]率先发展了俯仰阻尼导数、滚转阻尼导数和偏航阻尼导数的求解方法；文献[9-11]进一步完善了飞行器非定常计算的研究。

对于翼伞的气动性能的分析，国内学者做了很多研究；朱旭等分析了翼伞下反角、平面形状等设计参数对翼伞气动性能的影响[12-13]；汪龙芳等基于索膜有限元模型对翼伞气动变形进行分析[14]；黄炎等分析了前缘切口参数对大型冲压翼伞的性能的影响[15]。

国内外已有的文献还没有关于翼伞动导数的研究，因此本文率先提出采用滑移网格技术对翼伞气动特性中的俯仰阻尼导数、滚转阻尼导数以及偏航阻尼导数进行了计算，并比较了不同的减缩频率和攻角对翼伞阻尼导数的影响，得到了相关的结论，为翼伞动态气动特性的计算提供参考。

1 计算方法

1.1 控制方程

对于翼伞的动导数求取，需要求解非定常N-S方程，由于翼伞飞行速度低，计算时，空气可以作为不可压流处理。控制方程可以写为：

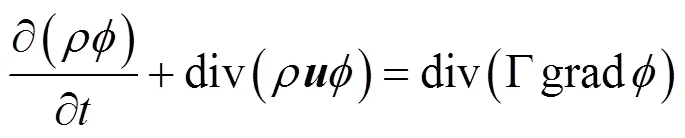
式中为速度矢量；为通用求解变量；G为广义扩散系数；为空气密度；为时间。

本文使用的湍流模型为SST–湍流模型，它综合了–模型远场计算的优点和–模型近壁区计算的优势，对适当的逆压梯度流动模拟有较好的预测。空间离散采用二阶迎风格式（Roe-FDS）。

1.2 滑移网格

相对于其它动网格技术，滑移网格不需要进行网格重构，节省了计算机资源，并且运动过程中整个计算域网格的品质不发生任何变化，避免了负体积网格的出现。滑移网格技术使用了两个或多个计算区域，每一个计算区域与相邻的区间至少存在一个分界面。相邻计算域形成“网格分界”的形式，在计算时，一个计算域相对另一个计算域可以沿着网格分界面滑动。通过恰当设置交界面的边界条件能够实现不同计算区域的数据交换。

图1 翼伞外形及稳定坐标系

1.3 动导数的求解

通过模拟翼伞小幅度运动可以计算翼伞的阻尼导数，动稳定性研究一般选择对称定直平飞状态作为参考状态，以俯仰方向上的求解为例，在稳定坐标系中定义小幅度俯仰运动，在参考状态下，飞行速度位于机体对称面内，则稳定坐标系与气流坐标系重合如图1所示。

翼伞绕过轴做周期性小幅度俯仰振荡振动，给定飞行器沿俯仰方向做定轴转动时的强迫振动方程：

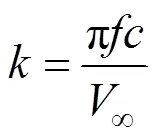
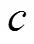
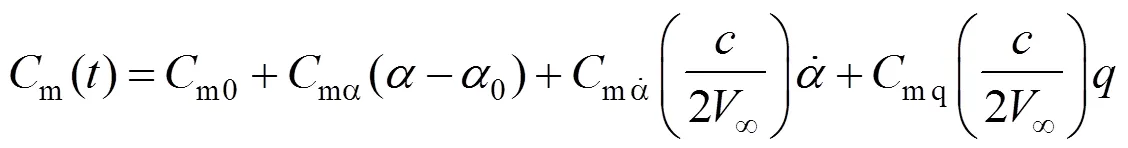
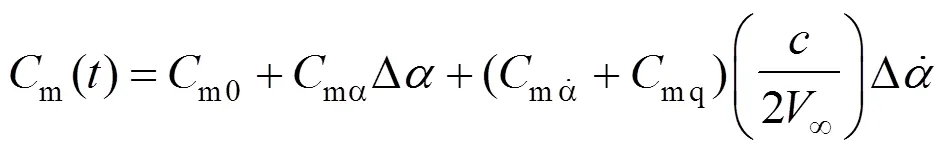
式中

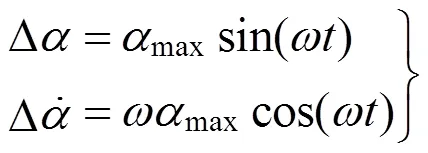
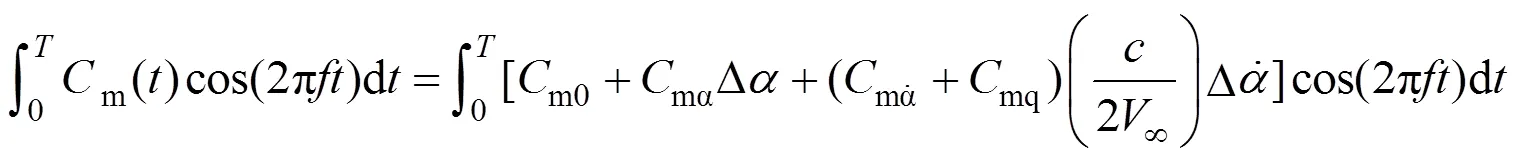
则可求得俯仰阻尼导数：

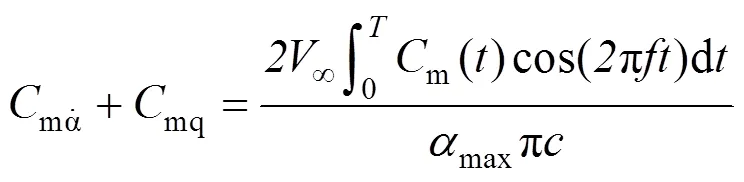
按照俯仰阻尼导数的求解方法，给定翼伞沿滚转方向做定轴转动时的强迫振动方程：

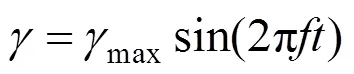
式中为滚转角度；max为滚转角度振动幅值。

则可以得到翼伞的滚转阻尼导数为：

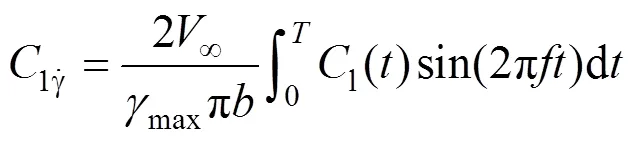
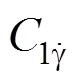
给定翼伞沿偏航方向做定轴转动时的强迫振动方程：

式中为偏航角度；max为偏航角度振动幅值。

可以得出翼伞的偏航阻尼导数为：

式中 Cn(t)为任意时刻下的偏航力矩系数；为偏航方向的动导数。

1.4 模型和网格

计算模型采用文献[17]中模型，采用滑移网格技术模拟翼伞定轴转动，在翼伞物面上生成高度较低的棱柱网格以满足边界层的要求，而在其他区域生成四面体网格，所有模型的网格均采用同样的方式生成，网格数目为230万。将计算域设定为立方体，各边界面距离模型均为15倍弦长，整个流场域分为静止域和滑移域两部分，其中滑移域是一个由物面包裹的球形流场域如图2所示，可以在稳定坐标系下做定轴转动，静止域为包围滑移域的区域。当模拟翼伞周期性俯仰振动时，整个物面内的网格一起运动。此时，物面内及物面网格不发生任何改变，将球面设置为可以和外流场进行数据交换的接触面。

为了简化对翼伞非定常气动特性的模拟计算，对于翼伞模型的计算做如下假设：翼伞为刚性，忽略气室“鼓包”现象以及气动扰动时的变形现象；伞衣材料不透气；忽略伞绳的影响；计算时不考虑伞衣的厚度。

2 结果分析

2.1 俯仰阻尼导数

边界条件如下：海平面零高度，来流速度为12m/s，为速度入口边界条件，出口为压力出口。假设翼伞初始情况下能够稳定飞行，在纵向平面内受外界微小扰动后，翼伞会产生小幅度俯仰振荡，给定翼伞按式（2）做小幅度振荡运动。

选取振动频率为0.1Hz、0.25Hz、0.5Hz，分别对攻角为0°、4°、8°、12°，振幅为4°的工况进行模拟计算，得到了翼伞做小幅度俯仰运动时俯仰力矩系数。

图3给出4°攻角时俯仰力矩迟滞曲线，分析图可知，动态俯仰力矩系数曲线在给定的不同频率下均呈“O”字形，且其变化趋势呈逆时针走向，产生负的俯仰阻尼导数；随着减缩频率的增大，非定常流动引起的俯仰方向的迟滞效应越明显，迟滞曲线的面积增加，会导致翼伞产生更大的俯仰阻尼导数。图4给出12°攻角时俯仰力矩迟滞曲线，分析图可知，在攻角为12°时，动态俯仰力矩系数迟滞曲线在给定的频率下呈“8”字形，并且在攻角8.0°<<10.5°范围内其变化趋势呈逆时针走向，在10.5°<<16.0°范围内时其变化趋势呈顺时针走向，且顺时针方向的迟滞环曲线所包围的面积大于逆时针方向迟滞环所包围的面积，导致翼伞产生正的俯仰阻尼导数。

根据式（8）可以计算翼伞的俯仰阻尼导数，图5给出俯仰阻尼导数计算的结果，由图可知，在小角度情况下，俯仰阻尼导数为负且其数值随着攻角的增加变化较小；而在攻角12°时翼伞的俯仰阻尼导数变为正，这是由于在攻角10.5°<<16.0°范围内做下俯运动时，伞处于动态失速情况，表面压力突变，俯仰力矩急剧下降，导致在相同攻角下下俯运动所产生的力矩系数小于上仰过程；在小攻角下，攻角相同时，翼伞的俯仰阻尼导数随着减缩频率的增加而减小。

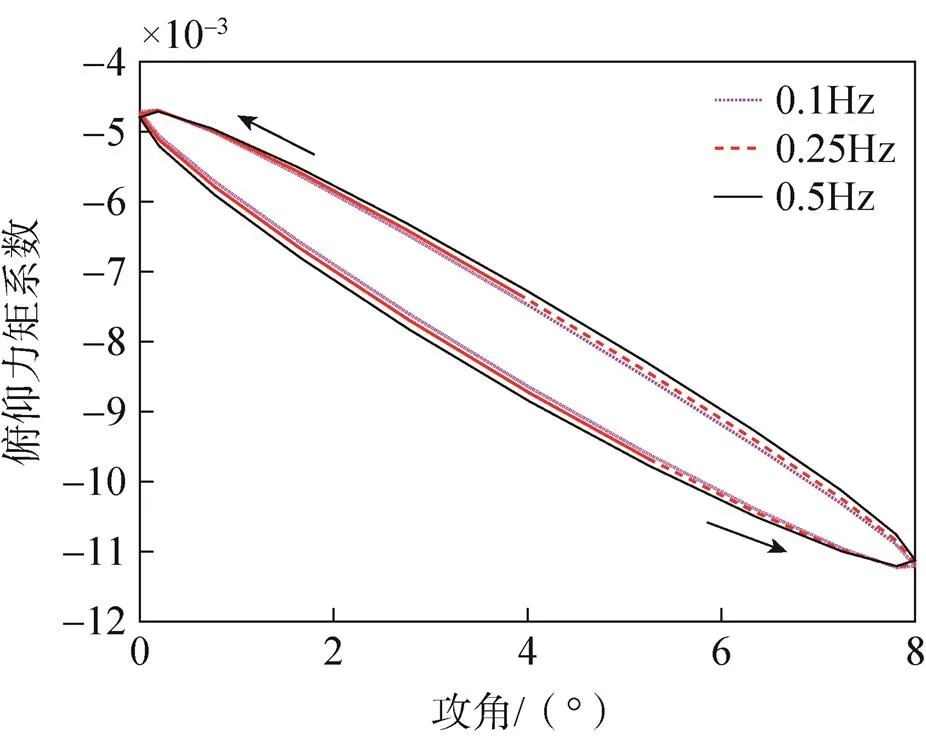
图3 a0=4°时俯仰力矩系数迟滞曲线

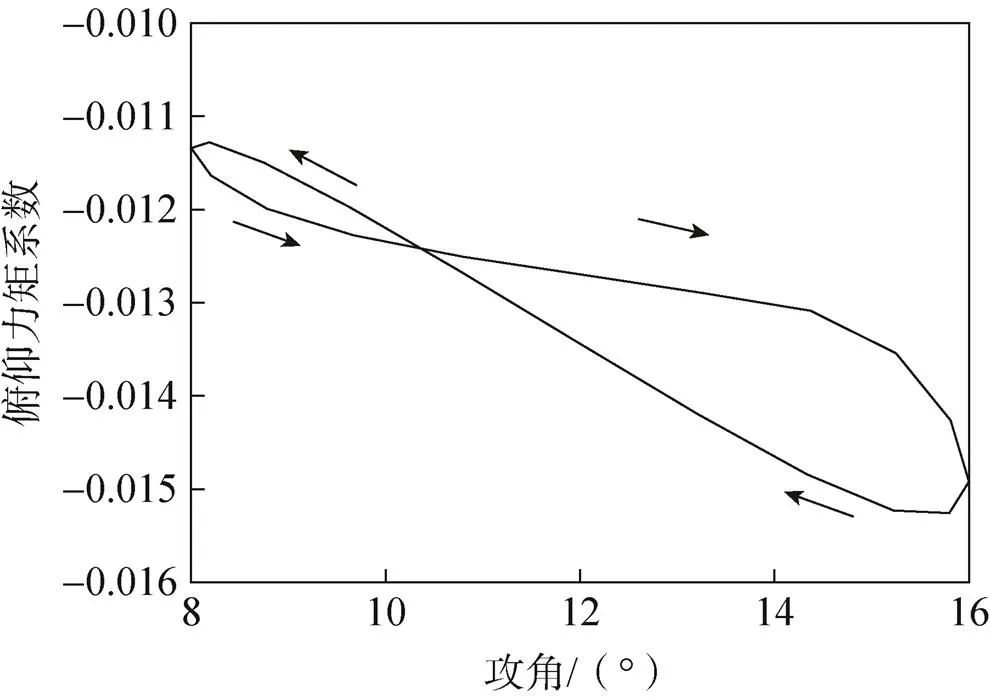
图4 a0=12°、f=0.5Hz时俯仰力矩系数迟滞曲线

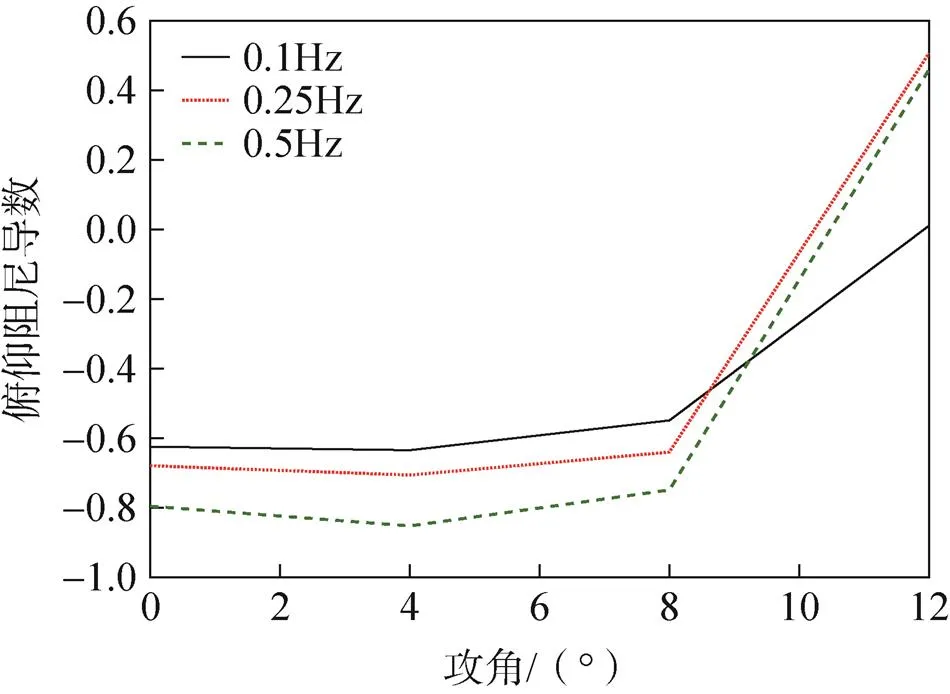
图5 俯仰阻尼导数随攻角变化

2.2 滚转阻尼导数的计算

一般来说，当飞行器做滚转运动时，会产生滚转阻尼，由于翼伞结构布局简单，只需考虑翼伞伞身对其滚转阻尼导数的影响。给定翼伞按式（9）做小幅度滚转运动。

采用2.1中的边界条件，得到了翼伞做小幅度滚转运动的迟滞曲线图。图6和图7分别给出在不同频率和攻角下的滚转力矩系数迟滞曲线。

分析图可得，非定常滚转力矩系数曲线在给定的频率和攻角下呈“O”字形，且其变化趋势呈逆时针走向，说明翼伞单独做滚转运动引起负的滚转阻尼导数；在同一个攻角下，随着减缩频率的增加，非定常流动所引起的滚转方向的迟滞效应越明显，翼伞具有更大的滚转阻尼导数。根据式（12）可以计算模型的滚转阻尼导数，图8给出滚转阻尼导数的计算结果。

由图可知，在攻角0.0°<<8.0°区间滚转阻尼导数随着攻角的增大线性增加；在攻角为12°时，由于翼伞在大攻角下伞衣表面存在复杂的分离流动导致滚转阻尼导数变小；在相同攻角下，随着频率的增加，翼伞的滚转阻尼导数变大。

2.3 偏航阻尼导数的计算

区别于平直翼，翼伞沿展向具有一定的弧度，在做偏航运动时会产生偏航力矩，给定翼伞按照式（11）做小幅度偏航运动。

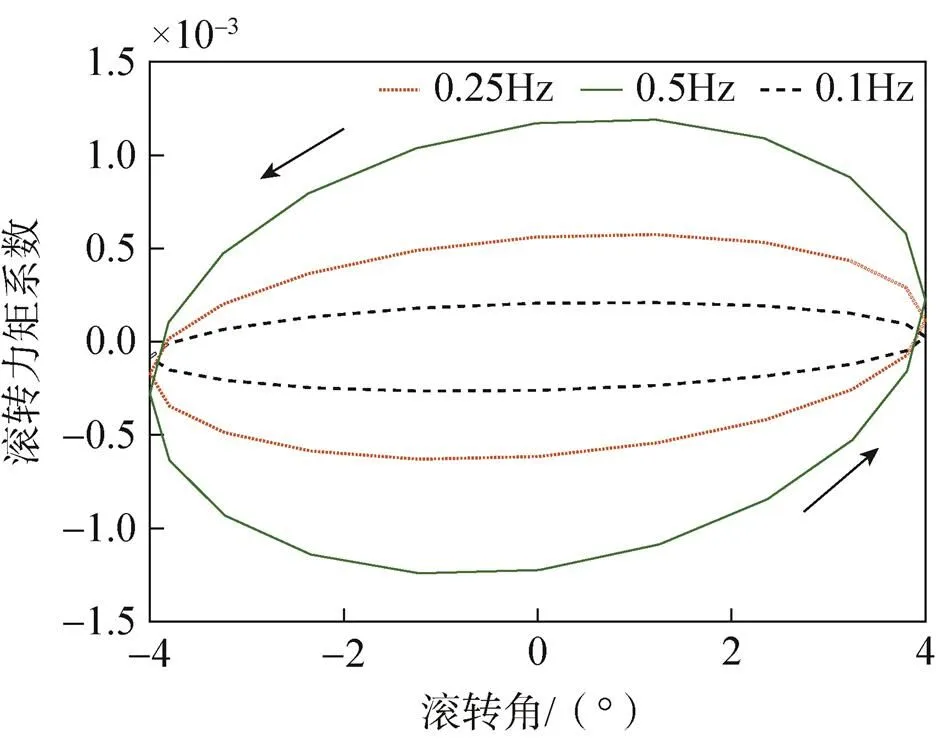
图6 a0=4°时滚转力矩系数迟滞曲线

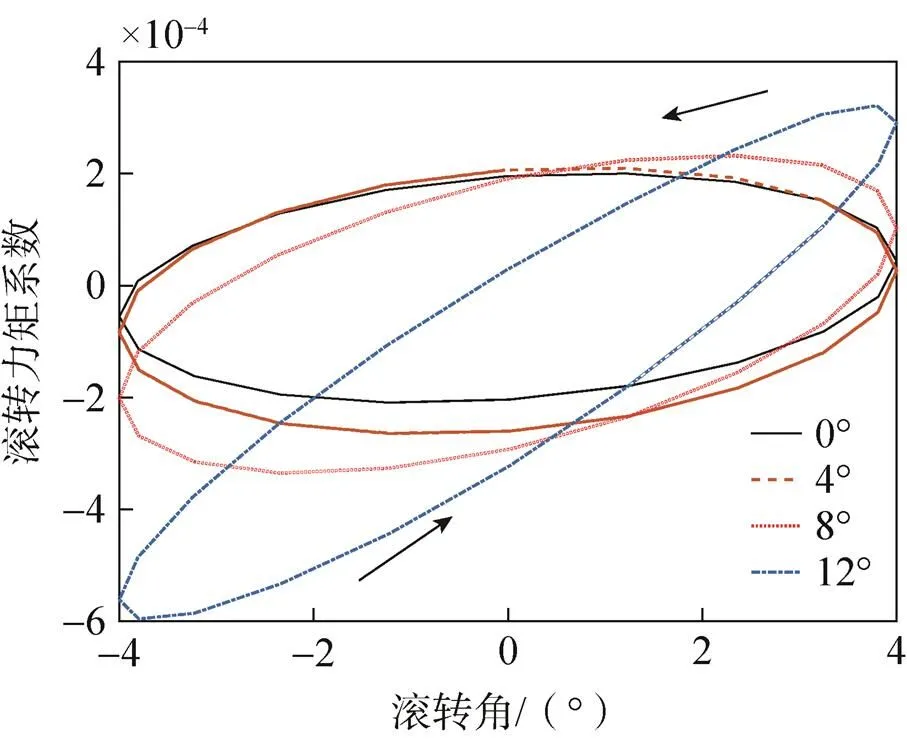
图7 f=0.1Hz时滚转力矩系数迟滞曲线

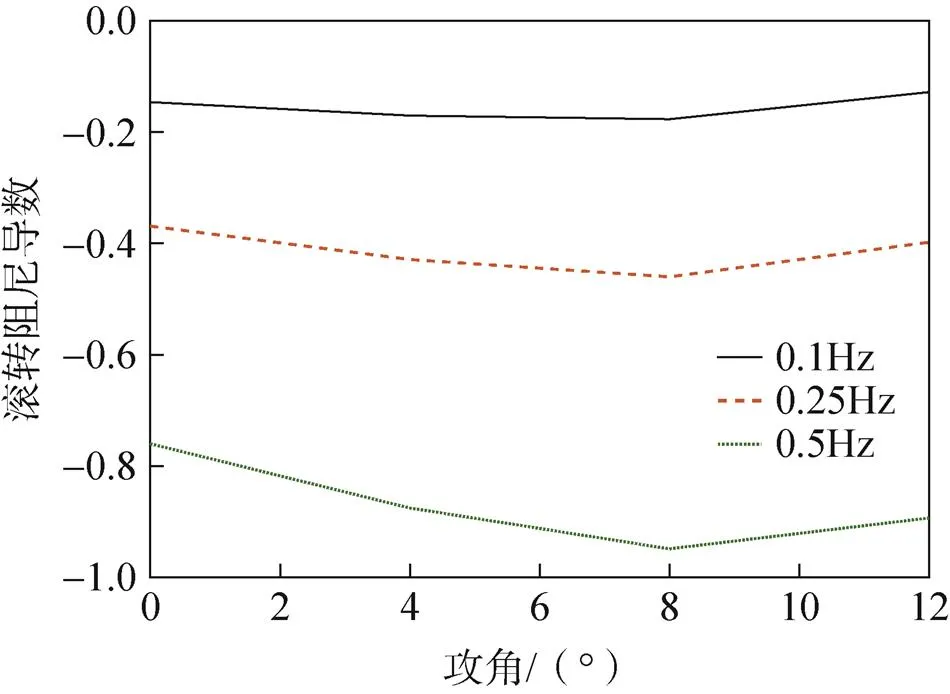
图8 滚转阻尼导数随攻角变化

采用2.1中的边界条件，得到了翼伞的做小幅度偏航运动的迟滞曲线图。图9和图10给出不同频率和攻角下的偏航力矩迟滞曲线。

图9 a0=4°时偏航力矩系数迟滞曲线

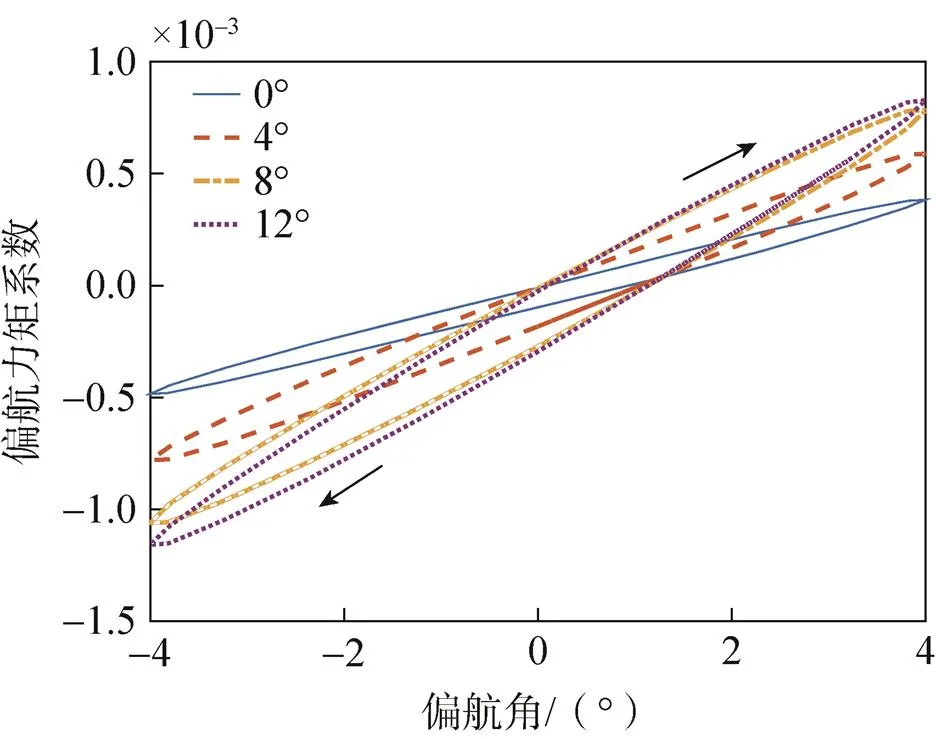
图10 f=0.1Hz时偏航力矩系数迟滞曲线

分析图可知，非定常偏航力矩系数曲线在给定的攻角下呈“O”字形，其变化趋势呈顺时针走向，模型单独做偏航运动所引起的偏航阻尼为正；在同一个攻角下，随着减缩频率的增加，非定常气动力引起的偏航方向迟滞效应变小，迟滞曲线包围的面积减小，翼伞在较大的减缩频率下会产生较小的正的偏航阻尼。

根据式（12）可以计算模型的偏航阻尼导数，图11给出偏航阻尼导数的计算结果。

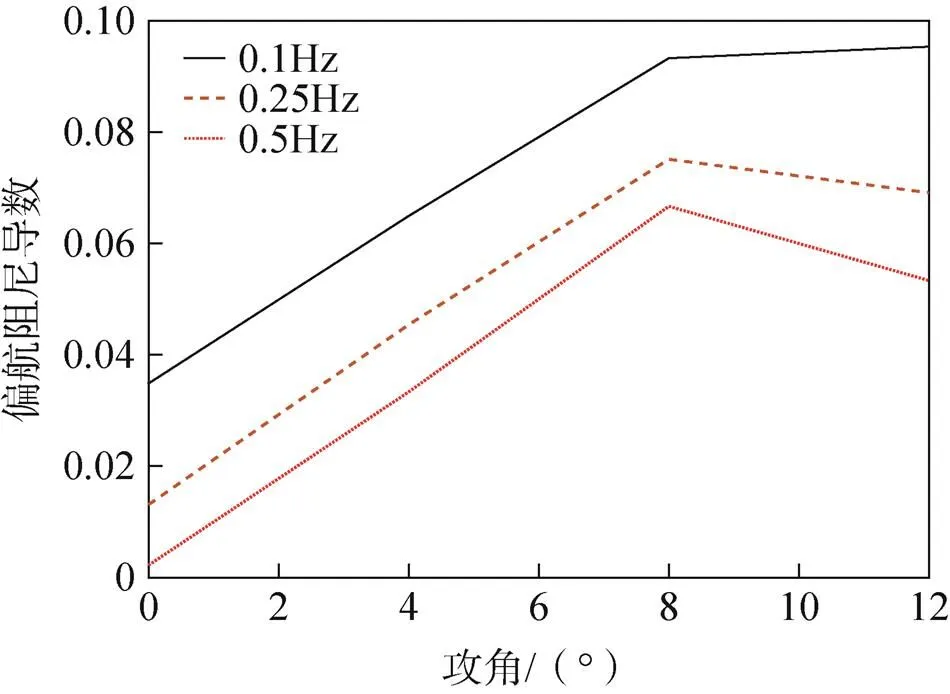
图11 偏航阻尼导数随攻角变化

由图可知，在0°到8°区间偏航阻尼导数随着攻角的增加线性增加，在攻角为12°时，翼伞伞衣表面存在复杂的分离流动造成偏航阻尼导数变小；在相同攻角下，随着减缩频率的增加，翼伞的偏航阻尼导数变小。

3 结束语

采用基于滑移网格技术的方法对翼伞的动导数的计算研究和分析，可以初步得到以下几点结论：

1）对于俯仰运动，攻角的增加不仅能影响迟滞环面积的大小还能影响迟滞环的动态特性，影响翼伞的动稳定性；减缩频率只改变动导数的数值而不改变动导数的正负性。

2）对于滚转运动，攻角变化对滚转阻尼导数影响较小，减缩频率的增加会使滚转阻尼导数成倍增加，在进行翼伞滚转阻尼导数计算时应正确的选择减缩频率。

3）翼伞在做单独的偏航运动时，其偏航阻尼导数为正，该翼伞不具有偏航方向上的动稳定性，在飞行时可以通过后缘下偏操作来改变偏航方向上的动稳定性。

[1] 童秉纲, 陈强. 关于非定常空气动力学[J]. 力学进展, 1983, 13(4): 377-394. TONG Binggang, CHEN Qiang. Some Remarks on Unsteady Aerodynamics[J]. Advances in Mechanics, 1983, 13(4): 377-394. (in Chinese)

[2] GREEN L, SPENCE A, MURPHY P. Computational Methods for Dynamic Stability and Control Derivatives[R]. AIAA 2004-0015, 2004.

[3] 刘绪, 刘伟, 柴振霞, 等. 飞行器动态稳定性参数计算方法研究进展[J]. 航空学报, 2016, 37(8): 2348-2369. LIU Xu, LIU Wei, CHAI Zhenxia, et al. Research Progress of Numerical Method of Dynamic Stability Derivatives of Aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2348-2369. (in Chinese)

[4] PARK S H, KIM Y, KWON J H. Prediction of Dynamic Damping Coefficients Using Unsteady Dual-time Stepping Method[C]//AIAA Aerospace Sciences Meeting & Exhibit, 2002.

[5] MURMAN S M. Reduced-frequency Approach for Calculating Dynamic Derivatives[J]. AIAA Journal, 2005, 45(6): 2005-2840.

[6] 刘伟, 牟斌. 类升力体俯仰阻尼特性数值研究[C]//第十届全国计算流体力学会议论文集. 绵阳, 2000: 381-386. LIU Wei, MOU Bin. Numerical Study of Damping-in-pitch Characteristics for Liftbody-type[C]//National Conference on computational fluid dynamics. Mianyang, 2000: 381-386. (in Chinese)

[7] 刘伟, 牟斌. 高超声速滚转阻尼导数数值模拟[J]. 飞行力学, 2000,18(2): 27-29. LIU Wei, MOU Bin. Numerical Simulation of Damping-in-roll Derivatives of Blunt Cone for Hypersonic Flow[J]. Flight Dynamics, 2000, 18(2): 27-29. (in Chinese)

[8] 刘伟, 瞿章华. 强迫振动法求解偏航阻尼导数[J]. 推进技术, 1998, 19(3): 30-32. LIU Wei, QU Zhanghua. Calculation of Damping-in-yaw Derivatives by Forced Oscillation Method[J]. Journal of Propulsion Technology, 1998, 19(3): 30-32. (in Chinese)

[9] 米百刚, 詹浩, 樊华羽. 飞行器组合及单独动导数数值求解方法研究[J]. 西北工业大学学报, 2015, 33(4): 540-545. MI Baigang, ZHAN Hao, FAN Huayu. Calculating Combined and Single Dynamic Derivatives of Flight Vehicle[J]. Journal of Northwestern Polytechnical University, 2015, 33(4): 540-545. (in Chinese)

[10] 孙涛, 高正红, 黄江涛. 基于CFD的动导数计算与减缩频率影响分析[J]. 飞行力学, 2011, 29(4): 15-18. SUN Tao, GAO Zhenghong, HUANG Jangtao. Identify of Aircraft Dynamic Derivatives Based on CFD Technology and Analysis of Reduce Frequency[J]. Flight Dynamics, 2011, 29(4): 15-18. (in Chinese)

[11] 苗伟. 飞机横向非定常气动力特性研究[D]. 南京: 南京航空航天大学, 2007. MIAO Wei. Research on Lateral Direction Unsteady Aerodynamic Characteristics of Aircraft[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2007. (in Chinese)

[12] 朱旭, 曹义华. 翼伞弧面下反角、翼型和前缘切口对翼伞气动性能的影响[J]. 航空学报, 2012, 33(7): 1189-2007. ZHU Xu, CAO Yihua. Effects of Arc-anhedral Angle, Airfoil and Leading Edge Cut on Parafoil Aerodynamic Performance[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(7): 1189-1200. (in Chinese)

[13] 朱旭, 曹义华. 翼伞平面形状对翼伞气动性能的影响[J]. 航空学报, 2011, 32(11): 1998-2007. ZHU Xu, CAO Yihua. Numerical Simulation of Platform Geometry Effect on Parafoil Aerodynamic Performance[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(11): 1998-2007. (in Chinese)

[14] 汪龙芳, 贺卫亮. 基于索膜有限元模型的翼伞气动变形仿真[J]. 北京航空航天大学学报, 2017, 43(1): 47-52. WANG Longfang, HE Weiliang. Parafoil Aerodynamic Deformation Simulation Based on Cable-membrane Finite Element Model[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(1): 47-52. (in Chinese)

[15] 黄炎, 张红英, 杨璐瑜, 等. 前缘切口参数对大型冲压式翼伞的性能影响分析[J]. 航天返回与遥感, 2017, 38(5): 10-17. HUANG Yan, ZHANG Hongying, YANG Luyu, et al. Analysis of Leading Edge Cut Parameters on Performance of Large Ram-air Parachute[J]. Spacecraft Recovery & Remote Sensing, 2017, 38(5): 10-17.(in Chinese)

[16] ETKIN B. Dynamics of Flight: Stability and Control[M]. New York and London: John Wiley and Sons, Inc., 1959.

[17] 汪龙芳, 贺卫亮, 王世超. 伞衣透气性对翼伞气动特性的影响[J]. 北京航空航天大学学报, 2017, 43(10): 2021-2029. WANG Longfang, HE Weiliang, WANG Shichao. Effects of Canopy's Air Permeability on Parafoil Aerodynamic Performance[J]. 2017, 43(10): 2021-2029. (in Chinese)

[18] JANN T. Aerodynamic Coefficients for a Parafoil Wing with Arc Anhedral-theoretical and Experimental Results[C]//17th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar. California, 2003.

Calculation of Dynamic Derivatives for Parafoil Based on Sliding Mesh Technique

WANG Shichao HE Weiliang

（School of Astronautics, Beihang University, Beijing 100191, China）

Parofil in the field of spacecraft recovery has widely prospect. To improve the understanding of dynamic stability of the specific parafoil, the dynamic derivative of a type of parafoil is analyzed in this paper. Based on the Computational Fluid Dynamics(CFD), a three-dimensional numerical simulation was completed by using sliding mesh. The emphasis is on the analysis of the small amplitude pitch, yaw and roll oscillation. Furthermore, different angles of attack and the reduction of frequency are choose to achieve the hysteresis curve of moment coefficient, and a time average method was built to calculate damp dynamic derivative around three axes. The results show that when the parafoil moves in small amplitude oscillatory motion at small angle of attack, the dynamic derivative is negative in the direction of pitch and roll. It has the dynamic stability in pitch and roll direction. However, in the yaw direction, the dynamic derivative is positive which means that it is unstable. Angle of attack and the reduce frequency would affect the dynamic derivative of parafoil, the increment of angle of attack can not only affect the size of hysteresis loop but also the dynamic characteristics of hysteresis loop, thus changing the dynamic stability. However, reducing frequency only affects the size of hysteresis loop, the dynamic stability will not change.

sliding mesh; reduce frequency; angle of attack; dynamic derivative; parafoil; spacecraft recovery

V411.3

A

1009-8518(2018)05-0034-08

10.3969/j.issn.1009-8518.2018.05.005

王世超，男，1992年生，2015年获北京航空航天大学飞行器设计专业学士学位，现在北京航空航天大学宇航学院攻读硕士学位。研究方向为飞行器设计。E-mail：846089241@qq.com。

2017-10-17

（编辑：庞冰）